我国电力企业越来越重视需求侧的互动和服务,用户也初步具备了参与电网公司开展需求响应工作的意愿,需求响应强化了用户与电网的交互能力,更有利于挖掘用户侧的调节能力[1-3]。由于电力系统需要保持灵活敏捷的调控能力,从需求侧进行负荷可调度能力的分析,有助于电网侧高效解决负荷峰谷差的问题,改善用户用电,达到削峰填谷的作用[4]。为了支撑更多终端资源参与到电网企业提供的可调节负荷相关互动与服务中,以及解决云计算中心海量的电力数据的问题[5],提出了边缘计算模式的融合[6]。边缘计算模型将计算分析功能扩展到网络边缘侧一些具备计算能力的设备,只需要将计算分析结果上传至云中心,即可很大程度上减轻云计算中心的压力。
近年来,国内外研究人员在负荷可调节潜力方面进行了大量研究,主要是集中在温控负荷的建模以及调节能力评估上。文献[7]提出了一种基于温度预报的户用电采暖负荷可调节能力的评估方法,引入基于数值天气预报获取未来一定时间段内的温度参数, 评估了在满足人体舒适度的温度区间下的户用电采暖负荷的可调节能力。文献[8]针对灵活可调的负荷,建立了电热负荷参数的均匀聚类模型,分析了其调节电热负荷聚类的潜力。文献[9]针对电动汽车和空调,提出了一种粒子群算法,通过该算法进行了柔性负荷可调度潜力策略研究。文献[10]建立了一种基于实时电价下的用户可调节能力模型,解决了供电与用电间的电力供需不平衡问题,实现用户积极响应及利益最大化。文献[11]针对不同用户响应行为的不确定性、响应时延等问题,提出了一种基于需求响应信息物理系统的耦合特性,对用户可调节潜力和聚合商调度可靠性进行了建模。文献[12]考虑用户负荷特性和可调节潜力的用户用电行为,提出了一种融合K-means和自组织映射(Self-Organizing Maps,SOM)进行二次聚类综合聚类的方法。部分研究学者认为,在台区开展可调节潜力分析具有重要的意义,但需要考虑大规模用户负荷在不同时间维度下所展现的动态调节潜力的分析,目前相关研究工作正在开展。围绕影响调节潜力的共性因素,本文提出一种面向台区大规模用户负荷进行潜力分析研究的方法,采用边缘计算的模式,依靠长短期记忆(Long Short-term Memory,LSTM)神经网络算法评估不同维度下的用户终端可调节潜力,并通过算例仿真分析验证了该方法的可行性与有效性。
1 基于边缘计算的台区可调节潜力分析架构在传统台区内,由于缺乏智能化的方法和设备,导致边缘侧计算能力较弱,无法支撑边缘计算模型以及进行大规模的负荷可调节潜力分析。因此,在台区内最重要的是安装智能配变终端[13]。基于边缘计算能力的台区智能融合终端是配电台区以及用电侧的边缘物联节点,具备海量数据存储及强大的边缘计算能力,可以分担主站功能,实现对用户和包括电能表在内的用采终端的管控,实现信息实时的互联互通,推动营配贯通。
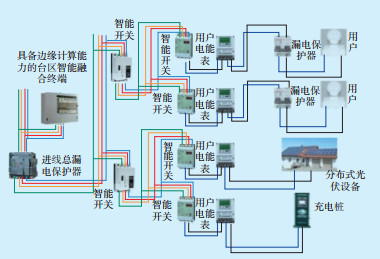
1.1 台区电气连接架构智能化终端设备采用“硬件平台化,软件APP化”的设计理念,配电台区作为数据汇聚和边缘计算中心[14]。根据智能配变终端功能及定位,提出基于边缘模式下台区电气连接架构图,如图 1所示。
|
| 图 1 基于边缘计算台区结构示意图 Figure 1 Structure diagram based on edge computing platform |
用户侧作为数据源头,主要功能是生产数据和执行决策。线路侧主要由智能开关构成,以便实现边缘计算赋能和统一通信能力。配变侧主要由智能配变终端、台区总表、进线总漏电保护器、进出线柱头等构成。智能配变终端是具备边缘计算能力的边缘物联节点,将基站功能与终端集成为一体。
在边缘侧对智能电能表、监测设备采集的数据进行就地分析处理并提供就地决策,实现设备管理、单元能效优化、台区管理等功能,以提高管理效率和满足实时性要求。对于设备预测能力及其维护等需要在云端进行数据处理、分析和训练。训练模型可在边缘智能设备中定期更新,以提供更精准的决策。
1.2 融合边缘计算的智能分析系统架构融合边缘计算的智能分析系统架构如图 2所示。该系统主要包括数据采集终端、边缘智能处理单元和云中心三个模块。数据采集终端将历史数据和实时数据采集上传处理,为边缘计算提供数据支撑。边缘智能处理单元主要处理实时轻量型数据,对数据进行存储处理之后,将模型训练数据上传至云中心。云中心适合处理非实时性、复杂度高的数据,主要对历史数据进行LSTM算法模型训练,并将训练好的模型移植到边缘智能处理单元中,通过边缘处理单元存储实时数据进行边缘计算,进而完成可调节潜力的实时分析。
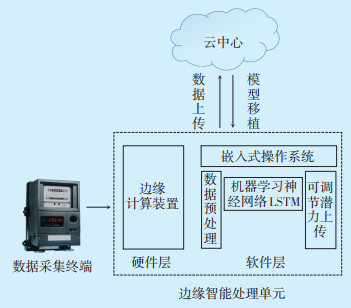
|
| 图 2 融合边缘计算的智能分析系统架构 Figure 2 Intelligent analysis system with edge computing |
融合边缘计算的智能分析系统将云中心的部分功能下放到边缘侧,边缘计算既能够减轻云中心的数据流量压力,又能够提高数据处理效率,实现可调节潜力分析的高实时性和低时延特性。
2 基于边缘计算的负荷调节潜力算法 2.1 LSTM神经网络算法原理LSTM深度神经网络属于循环神经网络(Recur-rent Neural Network,RNN)的一种,当前输出不仅与当前输入相关,还与RNN之前的输出有关,即此刻状态与上一刻的历史状态有一定程度的关系,且可能导致下一刻状态的变化[15]。
LSTM网络有三个门结构,分别是输入门,用于控制信息输入;遗忘门,用于控制细胞历史状态信息的保留;输出门,用于控制信息输出[16]。激励函数σ使得遗忘门的输出值在[0, 1],当遗忘门输出为0时,表示上一状态的信息全部丢弃;当遗忘门输出为1时,表示上一状态的信息全部保留,其涉及的过程和公式如下:
遗忘门:

|
(1) |
输入门:
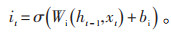
|
(2) |
记忆单元状态:
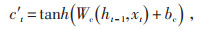
|
(3) |
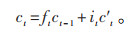
|
(4) |
输出门:
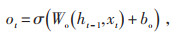
|
(5) |
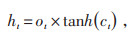
|
(6) |
式中:ht - 1为t-1时刻的输出数据;xt为t时刻的输入数据;ct - 1为t-1时刻的细胞状态;ft为遗忘门系数;it为输入门系数;c′t为通过tanh函数得到的输入数据;ct为t时刻更新后的细胞状态;ot为输出系数;ht为t时刻的输出数据;σ为sigmoid函数;Wf和bf分别为t-1时刻到达t时刻的神经元所对应的遗忘门的权重和偏置;Wi和bi分别为t-1时刻到达t时刻的神经元所对应的输入门的权重和偏置;Wc和bc分别为t-1时刻到达t时刻的神经元所对应的输入数据的权重和偏置;Wo和bo分别为t-1时刻到达t时刻的神经元所对应的输出门的权重和偏置。
由于LSTM神经网络具有特殊的门结构和记忆功能,可以避免传统RNN梯度消失问题[17-19],且可以记忆数据的长期依赖关系,非常适用于处理具有时间相关性的序列信息[20]。
基于LSTM的神经网络训练步骤如下:
(1)将t时刻数据特征输入输入层,经过激励函数输出结果;
(2)将输入层输出结果、t-1时刻隐藏层输出结果和t-1时刻Cell单元存储的信息输入LSTM结构的节点中,通过输入门、输出门、遗忘门和Cell单元的处理,输出数据到下一层隐藏层或输出层;
(3)将LSTM结构节点的输出结果代入输出层神经元,输出结果;
(4)误差反向传播,更新各个权值。
2.2 负荷调节潜力评估方法对于电力负荷的可调节潜力分析评估,采用数据分析与负荷预测融合的方法开展研究[21]。首先对原始数据特征进行选取,提取台区内家庭用户正常生活的电气数据,并且进行预处理,消除不同量纲的影响,选择与负荷可调节潜力高度相关的状态变量作为输入变量。其次是LSTM预测模型训练过程,将采集处理之后状态变量作为输入变量,电力负荷作为输出,接着对LSTM网络进行训练[22],通过迭代更新权值和偏置使误差最小,获得负荷功率预测模型。最后,进行负荷调节潜力计算,采用两种方法、两个维度进行可调节潜力分析处理:方法一,直接对历史负荷数据进行数学计算,量化为可调节潜力,再利用历史负荷可调节潜力数据进行预测;方法二,先将历史负荷数据进行预测分析,再利用数学方法进行潜力分析。在不同方法分析过程中,采用特征对比明显的时间段进行潜力分析会更加准确,因此利用时间维度对负荷数据进行划分,维度一采用不同月份之间的负荷数据,维度二采用工作日与节假日之间的负荷数据,以提高模型的适用性。
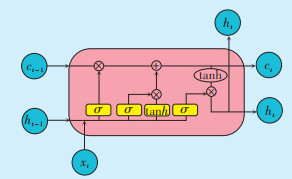
|
| 图 3 LSTM神经元内部结构 Figure 3 Internal structure of LSTM neurous |
LSTM算法模型一共5层,包括两个LSTM层、两个dropout层和一个全连接层。第一层LSTM网络中隐藏层的神经元个数设置为80,第二层LSTM网络中隐藏层的神经元个数设置为100,模型的损失函数设置为预测结果与实际值的均方误差,并采用Adam优化器。LSTM模型的训练参数见表 1。
| 表 1 LSTM模型训练参数 Table 1 Parameters of LSTM training model |
为评价电力可调节能力预测模型的性能,评价指标选择均方根误差(Root Absolute Error,RMSE),式中记作RMSE、均方误差(Mean Square Error,MSE),式中记作MSE,各评价指标的计算公式分别如式(7)、式(8)所示:
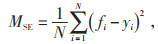
|
(7) |

|
(8) |
式中:fi,yi分别为某个时刻负荷实际值、预测值,其中i=1,2,…,N,N为数据集时间序列的长度。在预测模型评价指标中,MSE是指参数估计值与参数真实值之差平方的期望值;RMSE是均方误差的算术平方根。MSE和RMSE可以评价数据的变化程度和预测结果的准确性,MSE和RMSE的值越小,说明预测模型描述试验数据的精确度越高。
2.2.2 负荷可调节潜力计算流程综合考虑上述算法特点,提出了基于LSTM深度学习算法的负荷潜力评估模型。该计算模型主要包括三个过程:数据采集处理过程、LSTM预测过程和负荷潜力分析评估过程。具体流程图如图 4所示。
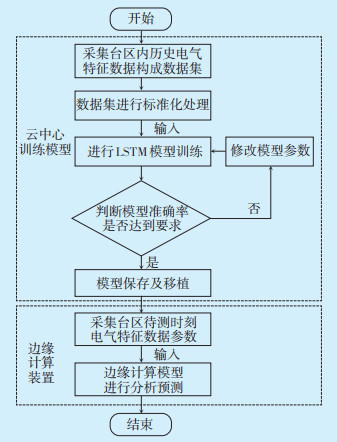
|
| 图 4 基于LSTM模型的潜力分析流程图 Figure 4 Flow chart of potential analysis based on LSTM model |
基于边缘计算模式的负荷可调节潜力的计算方法主要包括以下步骤;
(1)在台区内安装边缘计算装置,利用边缘计算装置采集不同用户、不同时刻、不同类别的电气特征参数作为模型训练测试数据集;
(2)对数据集进行标准化处理;
(3)选取与待测时刻的电气特征参数同一类簇的历史数据作为云平台预测模型的训练样本,通过LSTM神经网络算法进行训练,得到台区负荷潜力预测模型,训练完成后使用sklearn数据库提供的pickle函数将模型每一层的结构、权重和偏置及映射关系等参数进行保存;
(4)将保存的分析模型移植到边缘计算的终端设备中,并通过实时待测电气参数的驱动,得到实时负荷潜力曲线。
3 算例分析验证 3.1 算例说明为了验证LSTM模型在电力负荷调节潜力方面应用的可行性与有效性,本文选取某地区实际电力负荷数据部分样本(每15 min一个采样点,每日96点,量纲为MW)进行算例分析。按照前文所述两种方法、每种方法两个维度进行展开,采用2014年8月与1月的10户电力负荷数据进行维度一分析,以2014-09-26—09-30电力负荷数据为工作日样本数据,以2014-10-01—10-05电力负荷数据为节假日样本数据进行维度二分析。
经过训练集多次迭代,得出最优负荷可调节潜力预测模型,使用该模型对测试集进行预测,所得预测曲线如图 5所示。由图 5可知,LSTM模型的预测结果接近实际曲线,精确度较高。
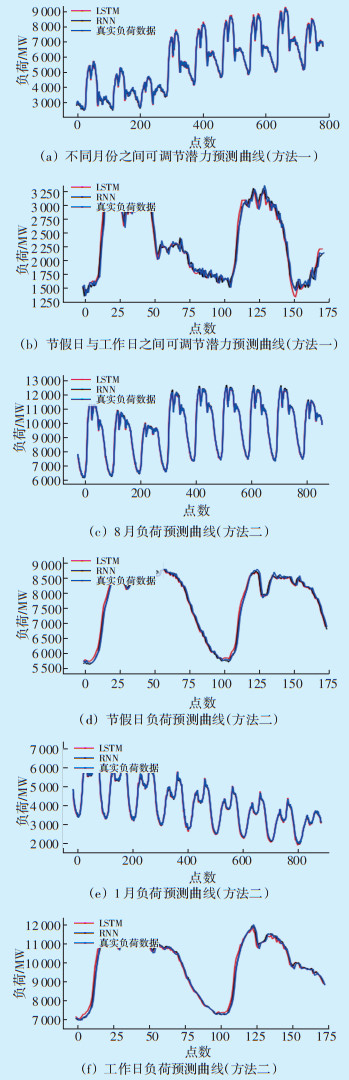
|
| 图 5 各维度负荷预测曲线 Figure 5 Load predication curve of each dimension |
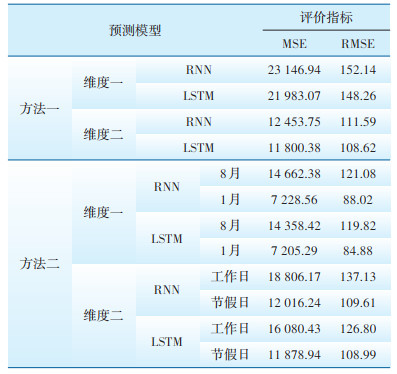
为了进一步验证LSTM模型的预测性能,分别计算RMSE、MSE值,将LSTM模型与RNN模型预测结果进行对比,见表 2。在使用相同方法、相同维度、不同模型的情况下,评价指标会呈现不同程度的差异。在方法一、维度一情况下,LSTM模型比RNN模型的MSE指标下降了5.3%,RMSE指标下降了2.6%;在方法一、维度二情况下,LSTM模型比RNN模型的MSE指标下降了5.5%,RMSE指标下降了2.7%。在方法二、维度一情况下,8月与1月结果中,LSTM模型比RNN模型的MSE指标分别下降了2.1%和0.3%,RMSE指标分别下降了1.1%和3.7%;在方法二、维度二情况下,节假日与工作日结果中,LSTM模型比RNN模型的MSE指标分别下降了16.9% 和1.2%,RMSE指标分别下降了8.1% 和0.6%。综上所述,LSTM模型的MSE、RMSE值分别比RNN模型都有不同程度的降低,验证了LSTM模型在电力负荷可调节潜力预测上具有良好的适用性。在仿真环境下,LSTM预测模型精度较高,为负荷可调节潜力的进一步深入分析奠定了基础。
| 表 2 两种预测模型的评价指标比较 Table 2 Evaluation indexes of the prediction model |
由于受温度、天气等众多因素影响,相对来说8月负荷数据要高于1月数据。将数据集前20 d数据划分为训练集,后10 d数据划分为测试集,利用该数据训练测试,得到不同月份之间调控能力的曲线图如图 6所示。
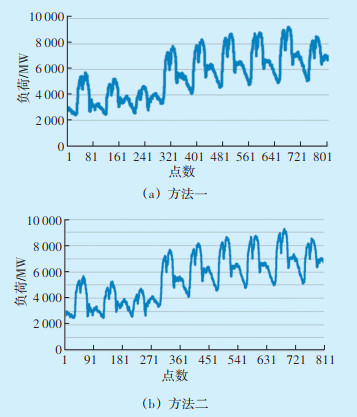
|
| 图 6 不同月份可调节能力曲线 Figure 6 Adjustable capacity curve of different months |
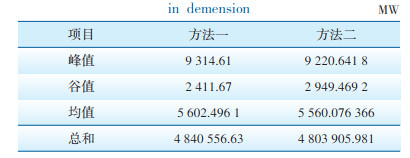
分别从调节潜力的峰值、谷值、均值和总和方面对两种方法进行比较分析,结果见表 3。可以看出,在不同月份可调节潜力峰值方面,方法二比方法一降低了93.969 MW,均值降低了42.421 MW。两种方法进行潜力分析的结果差异不大。
| 表 3 维度一不同方法结果比较分析 Table 3 Comparative analysis of results of different methods in demension |
由于测试样本绝大部分为家庭用电数据,因此节假日比工作日负荷相对要高,采用5 d数据,由前3 d数据训练,测试后2 d数据,得到工作日与节假日调控能力的曲线图如图 7所示。
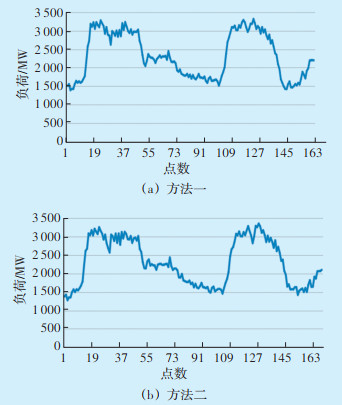
|
| 图 7 节假日与工作日可调节能力曲线 Figure 7 Holiday and working day adjustable capacity curve |
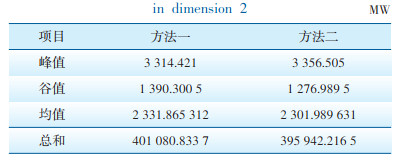
分别从调节潜力的峰值、谷值、均值和总和方面对不同方法进行比较分析,结果见表 4。由表 4可以看出,在节假日与工作日可调节潜力峰值方面,方法一比方法二降低了42.084 MW;方法二比方法一均值降低了29.876 MW。两种方法进行潜力分析的结果差异不大。
| 表 4 维度二不同方法结果比较分析 Table 4 Compartive analysis of results of different methods in dimension 2 |
本文提出了一种基于边缘计算的LSTM负荷可调节潜力分析模型。相比传统RNN方法,本文方法具有如下优势:
(1)针对可调节潜力分析需求,提出了基于边缘计算的方法,利用机器学习模型,自上而下对数据进行全面分析,提高数据分析的高效性、合理性和实时性。
(2)将与可调节潜力高度相关状态变量作为LSTM算法的输入变量,综合考虑选取两种不同时间维度进行分析,有效提高了电力负荷可调节潜力分析的准确性。
本文提出的基于边缘计算的台区负荷可调节潜力研究,与传统电网集中式对数据存储及潜力分析相比,很大程度上减轻了主站的数据处理压力,将算力边缘化,更加有效、实时处理数据,进而提高了电力负荷可调节潜力分析的准确性、实时性,为后续需求侧负荷研究提供了参考。
| [1] |
杨旭英, 周明, 李庚银. 智能电网下需求响应机理分析与建模综述[J].
电网技术, 2016, 40(1): 220-226 YANG Xuying, ZHOU Ming, LI Gengyin. Demand re-sponse mechanism analysis and modeling review under smart grid[J]. Power System Technology, 2016, 40(1): 220-226 (  0) 0)
|
| [2] |
闫华光, 陈宋宋, 杜重阳, 等. 智能电网电力需求响应标准体系研究与设计[J].
电网技术, 2015, 39(10): 2685-2689 YAN Huaguang, CHEN Songsong, DU Chongyang, et al. research and design of power demand response standard system for smart grid[J]. Power System Technology, 2015, 39(10): 2685-2689 (  0) 0)
|
| [3] |
王蓓蓓. 面向智能电网的用户需求响应特性和能力研究综述[J].
中国电机工程学报, 2014, 34(22): 3654-3663 WANG Beibei. A review of customer demand response characteristics and capabilities for smart grid[J]. Proceedings of the CSEE, 2014, 34(22): 3654-3663 (  0) 0)
|
| [4] |
吴震宇. 考虑净负荷峰谷差随机性的储能参与电网调峰配置与调度研究[D]. 长沙: 长沙理工大学, 2019.
(  0) 0)
|
| [5] |
LI. L. Cloud Computing Data Center Structure Based on Internet of Things and Its Scheduling Mechanism[C]//IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA). Dalian, China, 2020: 633-636.
(  0) 0)
|
| [6] |
K. Dolui, S. K. Datta. Comparison of edge computing implementations: Fog computing, cloudlet and mobile edge computing[C]//Mandat International. Global Internet of Things Summit (GIoTS). Switzerland, 2017: 1-6.
(  0) 0)
|
| [7] |
朱玉杰. 电采暖负荷可调节能力评估与集群控制策略研究[D]. 吉林: 东北电力大学, 2019.
(  0) 0)
|
| [8] |
HAN N H, GONG T R, GONG F X, et al. Evaluation and Cluster Control of Electric Heating Flexible Load Adjustable Capacity[C]//Sun Yat-sen University. Management Science Informatization and Economic Innovation Development Conference (MSIEID). Guangzhou, China: Sun yat-sen University, 2020: 425-428.
(  0) 0)
|
| [9] |
孙功伟, 周克楠, 马喆非, 等. 考虑柔性负荷的智能电网调度策略研究[J].
国外电子测量技术, 2020, 39(3): 40-46 SUN Gongwei, ZHOU Kenan, MA Zhefei, et al. Research on scheduling strategy of smart power grid with flexible load[J]. Foreign Electronic Measurement Technology, 2020, 39(3): 40-46 (  0) 0)
|
| [10] |
谈竹奎, 汪元芹, 赵菁, 等. 实时电价下用户侧电力需求响应模型优化策略及数字仿真[J].
电力大数据, 2020, 23(3): 10-18 TAN Zhukui, WANG Yuanqin, ZHAO Jing, et al. Optimization strategy and digital simulation of user-side power demand response model under real-time electricity price[J]. Power Systems and Big Data, 2020, 23(3): 10-18 (  0) 0)
|
| [11] |
任惠, 陆海涛, 卢锦玲, 等. 考虑信息物理系统耦合和用户响应差异的负荷聚合商需求响应特性分析[J].
电网技术, 2020, 44(10): 3927-3936 REN Hui, LU Haitao, LU Jinling, et al. Analysis of demand response characteristics of load aggregators considering information physical system coupling and user response difference[J]. Power System Technology, 2020, 44(10): 3927-3936 (  0) 0)
|
| [12] |
孙毅, 毛烨华, 李泽坤, 等. 面向电力大数据的用户负荷特性和可调节潜力综合聚类方法[J/OL]. 中国电机工程学报: 1-14. [2021-12-08]. https://doc.taixueshu.com/journal/20210559zgdjgc.xb.html.
SUN Yi, MAO Yehua, LI Zekun, et al. A Comprehensive Clustering Method of User Load Characteristics and Adjustable Potential Based on Power Big Data[J/OL]. Proceedings of the CSEE: 1-14[2021-12-08]. https://doc.taixueshu.com/journal/20210559zgdjgc.xb.html. (  0) 0)
|
| [13] |
YU L, QIU X W, KONG X J, et al. Research and improvement of integrated debugging method for intelligent distribution terminal[C]//IEEE. China International Conference on Electricity Distribution, Shanghai, 2012: 1-4.
(  0) 0)
|
| [14] |
宋耐超, 史雷敏, 王小雷, 等. 基于边缘计算模式的台区线损率计算方法[J].
上海电力大学学报, 2020, 36(5)471-476, 510 SONG Naichao, SHI Leimin, WANG Xiaolei, et al. Method for calculating transformer line loss based on edge calculation mode[J]. Journal of Shanghai University of Electric Power, 2020, 36(5)471-476, 510 (  0) 0)
|
| [15] |
曹渝昆, 巢俊乙, 王晓飞. 基于LSTM神经网络的风机齿轮带断裂故障预测[J].
电气自动化, 2019, 41(4): 92-95 CAO Yukun, CHAO Junyi, WANG Xiaofei. Prediction of wind turbine gear belt breakage based on the LSTM beural betwork[J]. Electrical Automation, 2019, 41(4): 92-95 (  0) 0)
|
| [16] |
M. Hajiaghayi, E. Vahedi. Code Failure Prediction and Pattern Extraction Using LSTM Networks[C]//2019 IEEE Fifth International Conference on Big Data Computing Service and Applications (Big Data Service). Nework, CA, USA, 2019: 55-62.
(  0) 0)
|
| [17] |
K. Goswami, A. Ganguly, A. K. Sil. Day Ahead Forecasting and Peak Load Management using Multivariate Auto Regression Technique[C]//Jadavpur University. 2018 IEEE Applied Signal Processing Conference (ASPCON) Kolkato, India: Jadavpur University, 2018: 279-282.
(  0) 0)
|
| [18] |
NIU P X, WANG Q, LI J C. Shortterm load forecasting model using support vector machine based on artificial neural network[C]//2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 2005: 4260-4265.
(  0) 0)
|
| [19] |
ZHOU K, ZHOU Y, DENG K. A circular recursion algorithm power load forecasting model and application[C]//Changsha University of Science&Technology. 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China: Changsha University of Science&Technology, 2019: 2870-2873.
(  0) 0)
|
| [20] |
YAO W Y, HUANG P, JIA Z X. Multidimensional LSTM Networks to Predict Wind Speed[C]//China University of Geosciences 201837 th Chinese Control Conference (CCC). Wuhan: China University of Geosciences, 2018: 7493-7497.
(  0) 0)
|
| [21] |
吴定安, 钟建伟, 王新磊, 等. 主成分分析和长短期记忆网络的电力负荷预测[J].
物联网技术, 2021, 11(8): 47-51 WU Dingan, ZHONG Jianwei, WANG Xinlei, et al. Power load forecasting based on principal component analysis and long short-term memory network[J]. Internet of Things Technologies, 2021, 11(8): 47-51 (  0) 0)
|
| [22] |
HU L, ZHANG L, WANG T, et al. Short-term load forecasting based on support vector regression considering cooling load in summer[C]//2020 Chinese Control And Decision Conference (CCDC). Northeastern University, 2020: 5495-5498.
(  0) 0)
|
 2022, Vol. 40
2022, Vol. 40