特高压输电线路在跨区域能源调度中起着非常重要的作用。然而由于特高压输电线路输送距离长,途经区域广,一旦线路发生故障会导致大范围停电,对电网的安全稳定运行造成不良影响。因此如何快速查找和消除故障是输电运检工作的重点和难点之一。
在输电线路故障检测定位方面,国、内外学者提出了故障分析法和单、双端行波法。故障分析法是由基本的电路参数计算得出故障位置,计算过程简单但效果较差。单端行波法利用故障点发出的行波进行定位,在行波传输过程中易出现衰减问题。相比于单端行波法,双端行波法不仅能够降低行波在传播过程中的衰减,而且更加可靠[1-2]。
进行行波故障定位时,线路长度是故障精准定位的重要影响因素。输电线路长度理论值与实际值存在差距[3],输电线路越长,理论值与实际值的误差越大。对于长达数千千米的特高压输电线路,其长度误差将产生非常大的影响。此外,输电线路过长也会导致行波在传播过程中出现衰减和畸变,易造成行波传播时间的误差,因此,缩短输电线路测距区间可以有效降低长度误差的影响,从而提高故障定位精度。
行波波速是导致故障定位误差的另一重要因素。部分文献论述线路故障定位时直接将行波波速按光速进行计算,易导致故障定位错误,加大巡检工作范围[4]。文献[3, 5-7]提出采用离线测量法、多组反射定位法和临近线路替代法等虽然能够在一定程度上获得近似的行波波速,但在特高压输电线路上产生的误差仍比较大。因此,获取精准的实时行波波速数据对故障定位精度的提高至关重要[8]。
鉴于输电线路长度和波速误差对传统行波法故障定位精度的影响,本文基于行波的传播特性,对误差来源进行分析,将分布式检测与行波法相结合,通过对故障相的相电流相位差动进行分析,从而确定故障发生区间和故障相,并提出基于分布式监测的特高压输电线路故障定位流程。
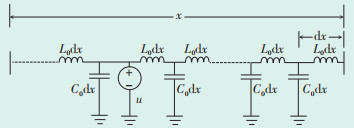
1 输电线路行波传播特性分析 1.1 行波传播过程行波传播的实质是输电线路上各个位置的分布电容和分布电感交替充放电的过程。研究行波在输电线路上的传导机制时,通常采用无损耗传输模型。如果单根输电线路发生故障,单根无损耗传输模型将在故障处增加电压源u,如图 1所示。
|
| 图 1 无损耗传输线模型 Figure 1 Lossless transmission line model 图中:x —输电线路长度;dx —单位长度;L0dx —单位长度上的电感;C0dx —单位长度上的电容。 |
附加电压源u向故障点两侧电容放电,电容电压升高,电容再向其旁侧的电感充电,电场能量与磁场能量实现交换。传输线路上电容与电感交替充放电,从而完成电信号的传播过程。
单位电场和单位磁场生成的速度为:
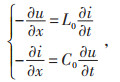
|
(1) |
式中:L0、C0分别为线路电感和电容;i为线路电流;t为时间。
1.2 相模变换实际输电线路为三相线路,将单相导线模型类推至三相耦合模型,则式(1)可以表示矩阵为:
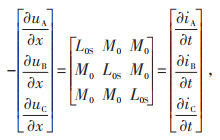
|
(2) |
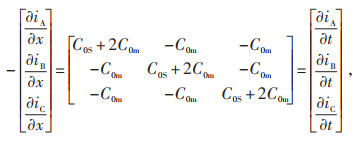
|
(3) |
式中:C0S为单相对地电容;C0m为单位相间电容;L0S为单相自感抗;M0为相间互感抗;iA、iB和iC分别为L1、L2、L3相电流。
为便于求解,对式(2)、式(3)电感、电容矩阵作变形处理,使其为对角阵;再对原始电压列向量u、电流列向量i进行解耦,结果分别记为电压解耦结果S、电流解耦结果Q,得到三相电压矩阵U与三相电流矩阵I为:
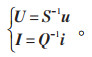
|
(4) |
将式(4)代入式(2)、式(3),并将其再次进行偏导微分后得:
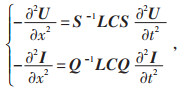
|
(5) |
式中:L、C分别为线路电感矩阵和电容矩阵。
相模变换实现对三相电压量和电流量解耦,计算出独立的线模分量与零模分量,从而可以检测到行波的到达时刻。
1.3 行波传播频变行波在传输过程中受环境等因素影响会不断衰减甚至畸变,导致监测的行波波头结果不佳,因此需要采用有损耗模型进行分析(见图 2)。因为有损耗模型中存在电阻R0和电导G0,行波的能量在行进中将被消耗。
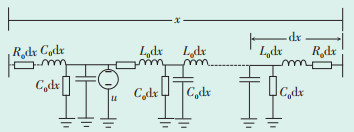
|
| 图 2 有损耗传输线模型 Figure 2 Lossy transmission line model 图中:R0dx —单位长度上的电阻。 |
输电线路的各个参数均与频率有关,通过相模变换将有损耗模型参数矩阵解耦为线模分量与零模分量。
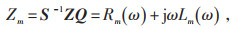
|
(6) |
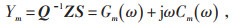
|
(7) |
式中:m=0,1,2,分别代表模域中0、1、2三种模态;Lm (ω)、Rm(ω)、Gm(ω) 和Cm(ω) 分别为输电线路单位长度随频率变化的电感、电阻、电导和电容;Zm为单位长度上的阻抗;Ym为单位长度上的导纳;ω为模域下的自变量;Z为阻抗矩阵。
与频率相关的波阻抗Zcm为:
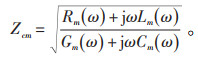
|
(8) |
模域下的传导系数γm为:
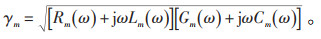
|
(9) |
模域下的行波波速vm为:
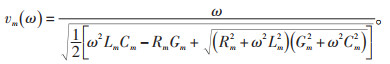
|
(10) |
输电线路长度理论值是线路设计规划时测定所得,通常为各杆塔之间的水平距离之和。理论值与输电线路的真实长度之间存在差距,弧垂程度、环境温度、负荷电流大小等因素都会影响输电线路的真实长度,其并不是一个确定值[9]。图 3所示为输电线路理论值与实际值比较。
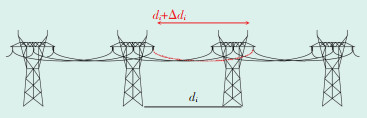
|
| 图 3 输电线路长度理论值与实际值对比 Figure 3 Schematic diagram of traveling wave reflection and refraction 图中:di—相邻杆塔的输电线路长度理论值(直线距离);di+Δdi—相邻两杆塔间输电线路长度实际值。 |
输电线路总长度的实际值是所有分段线路的实际长度之和,理论值与实际值之差ΔL为:
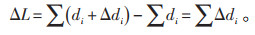
|
(11) |
采用双端行波法,利用行波至两端的时间差对tm、tn故障点进行确定:
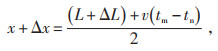
|
(12) |
式中:x为故障点到一侧端点的线路长度理论值;x + Δx为故障点到一侧端点的线路长度实际值;L为整条输电线路长度的理论值;L + ΔL为线路长度实际值;v为行波传播速度。
对式(12)进行移项,得:
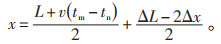
|
(13) |
假设分波波速正确无误差,式(13)右边被分成了两项,第一项为在无误差时得到的理论值,第二项为理论值与实际值之间的误差。误差大小与公式中Δx有关:当故障点距离端点的距离越大时,误差就进一步增大。百千米级的输电线路的长度误差为1%,其故障点定位误差可达500 m[10]。在实际行波传播过程中,除输电线路长度误差外,还受其他因素影响,将会造成更大的定位误差。
因此,在输电线路上增加分布式设备,将线路间距缩减为较短的测距区间,降低由线路长度误差产生的影响,能够有效降低行波在传播过程中的衰减和畸变,提高故障定位精度。
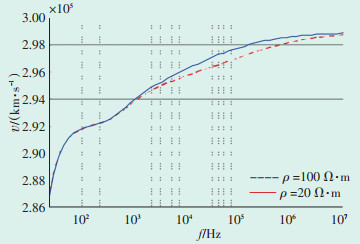
2.2 行波波速误差行波波速不仅与输电线路物理参数有关,还受行波中心频率和外部条件如土壤电阻率的影响。利用电磁仿真软件ATP-EMTP模拟行波在土壤电阻率分别为20 Ω·m、100 Ω·m的环境下线模波速随频率变化曲线,如图 4所示。
|
| 图 4 不同土壤电阻率下的线模波速图 Figure 4 Line mode wave velocity diagram under different soil resistivity |
由图 4可以看出,当频率升高时,线模波速会随之出现变化。土壤电阻率与土壤的温度和湿度有关[11],这就使得一段线路在不同的土壤状况下波速不同。所以要计算出正确的行波波速,在获得输电线路参数和行波中心频率后,还需要收集土壤电阻率等环境参数,这是难以实现的。
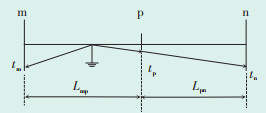
2.3 行波波速在线测量波速在线监测示意图如图 5所示。在输电线路监测点m点、n点的中点处,添加一个监测点p点,p点至m点及n点的水平距离已知。
|
| 图 5 波速在线监测示意图 Figure 5 Schematic diagram of wave speed online monitoring |
当m点至p点之间发生故障时,故障行波从故障位置分别进行左右传递,左侧行波直接到达m点,右侧行波将先通过p点,再传输至n点。
由于n点和p点两个监测点之间使用GPS进行对时同步,因此将两点之间的输电线路长度除以行波传播时间,则能够实现行波波速的实时监测:
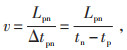
|
(14) |
式中:Lpn为p点至n点的线路长度理论值;tp为行波到达p点的时间;tn为行波到达n点的时间。
将式(14)代入式(13),得:
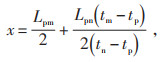
|
(15) |
式中:tm为行波到达m点的时间。
利用分布式监测设备,监测间距大大缩小,能够实时在线测量行波波速,有效降低波速误差导致的定位偏差。
2.4 分布式故障定位误差在应用分布式监测设备后,波速误差的影响虽然减小,但由于输电线路长度理论值与实际值仍有差距,因此对其误差的影响进行分析。以输电线路实际长度替代式(15)的理论值,移项后得:
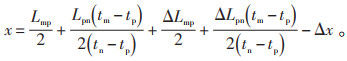
|
(16) |
将后三项记为定位误差项eL,则:
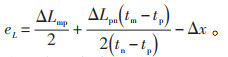
|
(17) |
当故障出现在m点附近时,Δx ≈ 0,此时定位误差为:
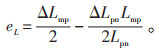
|
(18) |
当故障出现在p点附近时,Δx ≈ ΔLmp,此时定位误差为:
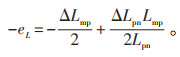
|
(19) |
由式(18)、式(19)可知,当Lmp≈ ΔLpn,即两端线路弧垂相等时,输电线路长度误差会被消除。虽然每段输电线路的弧垂各不相同,但分布式故障定位方法能够在一定程度上降低线路长度误差导致的故障定位误差。
3 故障定位分析 3.1 故障区间与故障相的判定采用分布式设备监测行波波速时,一般要将输电线路分成数段,故障定位前需对故障发生的区间进行判断。如果分布式设备所在区间离故障点较远,在线测得的行波波速不准确易导致定位失败,因此要通过故障发生处最近的3个分布式设备进行测量。寻找故障相也是输电线路故障定位的关键步骤,在故障发生后若能准确判断出故障相,就可以有针对性地检查某一相线路,尽快排除故障。
基于分相电流相位差动原理判断故障区间和故障相,具有简便有效的特点,在电力系统中已成熟应用。当异常电流出现后,故障电流分量不受电源自身相位差和线路阻抗的影响,在进行故障区间判断时更加可靠[9]。
分相电流相位差动原理如图 6所示。当m点至n点区段内发生短路故障时,假设从m点到n点方向的电流规定为正方向,理论上两端的电流故障分量相位差为180°;如果该区段或监测相未发生故障,理论上两端的电流故障分量相位差为0°。
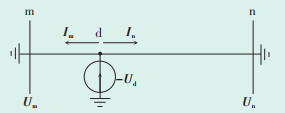
|
| 图 6 故障电流的相位差动原理示意图 Figure 6 Schematic diagram of phase difference principle of fault current |
故障发生时,线路电流可以看作正常状态电流量与故障分量的叠加,故障电流减去正常状态电流量即可获得电流故障分量:
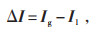
|
(20) |
式中:ΔI为电流故障分量;Ig为故障时的实际电流;I1为正常状态电流量。
从故障电流中提取出正常状态电流量很难,所以采用发生故障前一个周期的电流量代替:
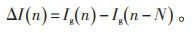
|
(21) |
式中:n为第n个采样点;N为一个工频周期的采样点数。
3.2 故障定位流程的制定基于上述原理,制订分布式监测设备的故障定位流程,如图 7所示。
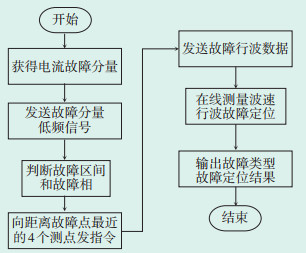
|
| 图 7 故障定位流程 Figure 7 Fault location flowchart |
(1)通过故障电流减去正常状态电流量,获得电流故障分量;
(2)监测电流故障分量大于阈值时,向监控站发送低频采样信号;
(3)基于电流相位差动原理判断故障区间和故障相;
(4)向故障点最近的4个监测点发出指令,使监测点向主站发送高频行波数据;
(5)进行行波波速在线测量和故障定位;
(6)输出故障定位结果和故障类型。
4 算例分析将行波波速解耦为零模分量和线模分量,利用电磁暂态仿真软件ATP-EMTP进行仿真分析。零模分量和线模分量频变曲线见图 8。当频率升高时,零模分量和线模分量均随之增长,当频率达100 Hz后,线模分量增速放缓并趋于光速;相比于线模分量,零模分量增速较缓,但始终保持增长,不会出现平台区。行波在导线上传播过程中会出现衰减,中心频率也因此下降,导致波速下降。由于零模分量的衰减性,线模分量通常被用于行波故障定位。
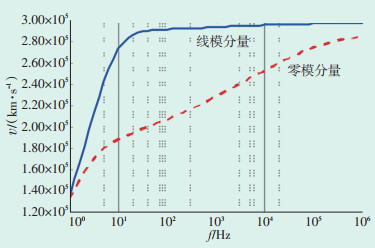
|
| 图 8 行波波速零模分量和线模分量频变曲线 Figure 8 Frequency variation curves of zero-mode and linear-mode components of traveling wave velocity |
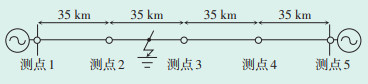
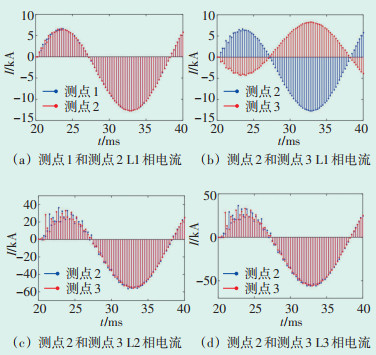
在ATP-EMTP软件中对1000 kV特高压输电线路进行仿真(仿真模型如图 9所示),设置线路长度为140 km,每35 km设置1个监测点,采样频率4 kHz,接地电阻为10 Ω。在测点2与测点3之间设置L1相接地故障,该故障点至测点2的距离为5 km。通过分布式监测设备获得离故障点最近的测点1、测点2和测点3的电流故障分量进行分析,比较同一区间两个监测点的电流故障分量,结果见图 10。当线路L1相发生接地故障后,电流故障分量迅速增加,三相中L1相的故障分量尤其明显,其他两相的故障分量较小。对比3个监测点的电流故障分量可知,测点2与测点3的L1相电流故障分量相位差为180°,其余测点的同相对比相位差均为0°,因此判断出故障区间为测点2至测点3,故障相为L1相。
|
| 图 9 1000 kV输电线路仿真模型 Figure 9 Simulation model of 1000 kV transmission line |
|
| 图 10 各监测点同相电流故障分量比较 Figure 10 Comparison of fault components of in-phase current at each monitoring point |
本文针对线路长度误差和行波波速误差对行波故障定位准确度的影响,提出基于分布式监测的输电线路故障定位方法,利用输电线路分布式检测设备实现行波波速的在线测量,既可以获取准确的行波波速数值,还可以有效降低特高压线路长度误差对故障定位的影响。此外,通过使用分布式在线监测设备,基于电流故障分量的分相电流相位差动原理,对故障区间和故障相进行判别,能够缩短故障定位时间。最后提出了基于分布式监测的故障定位系统的工作流程,并进行仿真分析,证明该故障定位方法的有效性。
| [1] |
田斌, 方覃绍阳, 李振兴, 等. 基于波速修正的多回输电线路行波测距算法[J].
高压电器, 2019, 55(1): 184-189 TIAN Bin, FANG Qinshaoyang, LI Zhenxing, et al. Parallel multiloop transmission line travelling wave location algorithm based on amending wave velocity[J]. High Voltage Apparatus, 2019, 55(1): 184-189 (  0) 0)
|
| [2] |
陈凤涛, 敬炳侠, 罗玉春. 输电线路单端行波测距法和双端行波测距法的对比[J].
电气技术与经济, 2020(增刊1)65-66, 75 (  0) 0)
|
| [3] |
刘亚东. 输电线路分布式故障测距理论与关键技术研究[D]. 上海: 上海交通大学, 2012: 29-41.
(  0) 0)
|
| [4] |
崔超奇. 基于暂态行波的输电线路故障定位研究[D]. 沈阳: 东北大学, 2019.
(  0) 0)
|
| [5] |
朱永利, 范国琛, 赵雪松, 等. 同杆双回输电线路的四点行波故障定位方法[J].
电力系统及其自动化学报, 2016, 28(12): 124-129 (  0) 0)
|
| [6] |
王育飞, 付玉超, 孙路, 等. 基于混沌-RBF神经网络的光伏发电功率超短期预测模型[J].
电网技术, 2018, 42(4): 1110-1116 WANG Yufei, FU Yuchao, SUN Lu, et al. Ultra-short term prediction model of photovoltaic output power based on Chaos-RBF Neural Network[J]. Power System Technology, 2018, 42(4): 1110-1116 (  0) 0)
|
| [7] |
夏远洋, 李啸骢, 陈飞翔, 等. 基于FastICA的输电线路行波故障测距方法[J].
电力系统保护与控制, 2019, 47(1): 138-143 XIA Yuanyang, LI Xiaocong, CHEN Feixiang, et al. FastICA based traveling wave fault location algorithm for transmission lines[J]. Power System Protection and Control, 2019, 47(1): 138-143 (  0) 0)
|
| [8] |
林丞. 基于分布式监测的输电线路故障定位方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
(  0) 0)
|
| [9] |
盛远. 混合输电线路行波故障测距分析与应用[D]. 北京: 中国矿业大学, 2019.
(  0) 0)
|
| [10] |
曹璞璘, 束洪春, 马仪, 等. 基于雷电定位系统与行波实测数据的雷击故障关联度分析[J].
中国电机工程学报, 2015, 35(20): 5220-5227 CAO Pulin, SHU Hongchun, MA Yi, et al. The correlation degree of lightning location system and measured field traveling wave data for lightning induced fault distinguishing[J]. Proceedings of the CSEE, 2015, 35(20): 5220-5227 (  0) 0)
|
| [11] |
郑智慧, 滕芸, 童雪芳, 等. 直流电流下土壤电阻率的变化规律及仿真研究[J].
武汉大学学报(工学版), 2020, 53(1): 5 (  0) 0)
|
 2022, Vol. 40
2022, Vol. 40

