0 引言

感应电动机（Induction Motor，IM）是电力系统中的重要动态负荷，在工业负荷中占比约90% ^[1]。精确掌握电动机的运行状态对保障电力系统的稳定运行具有重要意义。利用数字孪生（Digital Twin，DT）技术^[2]在虚拟空间建模，可实现对物理实体的状态监控与故障预警，已经广泛应用于电动机制造、电力物联网构建^[3-5]等领域，为电厂辅机系统高压大功率电动机的状态检测及故障预警提供新思路。

已有学者在电动机状态检测方面开展了大量研究，目前感应电动机检测方法主要包括传统有线监测、无线监测^[6-8]及基于智能算法的监测方法^[9-11]。针对传统监测方法需要布置众多传感器、接线繁琐等问题^[10]，文献[6]利用微型智能低功耗的传感器构建无线传感器网络系统，实现对电动机数据的无线监测，避免了大量布线，具有不受复杂环境影响且经济、方便等优点。在智能算法方面，文献[9]提出了一种四元数算法，结合电动机工况判据，仅需较小的样本即可精确判断电动机是否存在轴承故障或机械不平衡。文献[12]利用边缘计算技术，在靠近边缘设备处分析数据，仅传输少量数据至云端，有效降低了电动机故障无线监测的网络带宽成本。文献[13]提出了一种时域平均算法来准确监测故障特征。另外还有根据检测的物理量（如电流^[14]、振动 ^[15]、温度 ^[16]等信号）的监测方法。例如，文献[17-18]通过监测电流矢量判断电动机是否发生了故障；文献[19]通过电压瞬时频率监测感应电动机的轴承状态。综上所述，以往针对电动机工况辨识及故障预警的研究主要集中在无线监测、智能算法等方面，而将数字孪生技术运用于电动机检测的研究较少。

本文基于电动机经典电磁暂态模型，针对电厂辅机系统中的一台6 kV、1600 kW感应电动机进行数字孪生建模。实际应用结果表明，孪生模型能够快速、准确地识别电动机工况，验证了孪生模型适用于电厂辅机系统高压大功率电动机的实时状态监测。

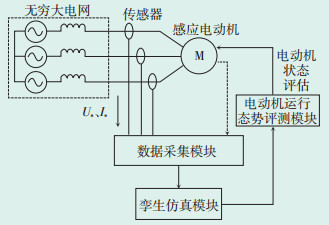
1 电动机数字孪生建模及算法 1.1 数字孪生系统结构

数字孪生模型不仅包含基于物理的微分代数模型，还包括基于数据驱动的模型，涉及内容较广。本文主要针对数字孪生模型的电气部分建模及其与实际电动机的数据交互开展研究，提出的电动机数字孪生系统包括感应电动机、数据采集模块、孪生仿真模块、电动机运行态势评测模块。其中数据采集模块用于采集电动机定子电流等关键信号；孪生仿真模块实现电动机的精确建模，并与实际电动机实时交互；电动机运行态势评测模块用于分析电动机运行工况并实现故障预警等功能。电动机数字孪生系统结构示意图如图 1所示。

1.2 感应电动机数学模型

为了便于采用粒子群算法辨识电动机参数，选取了定子电流、转子磁链、转速为状态变量。考虑到本文采用定子矢量图判断电动机运行工况，因此模型建立在静止αβ坐标系上。感应电动机状态方程如式（1）—式（4）所示。

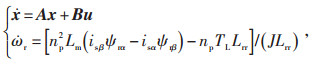
(1)

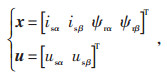
(2)

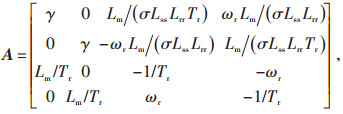
(3)

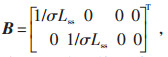
(4)

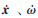
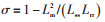
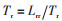
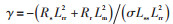
式中：x为状态变量；A为系统矩阵；B为输入矩阵；u为输入矢量；分别表示 x、ω的导数；i_sα、i_sβ、ψ_rα、ψ_rβ分别为α、β轴定子电流分量与转子磁链分量；u_sα、u_sβ为α、β轴定子电压；ω_r为电角速度；R_s、R_r分别为定转子电阻；L_ss、L_rr分别为定、转子总电感；L_m表示定转子互感；n_p为极对数；J为转动惯量；σ为漏感系数，；T_r为转子时间常数，；γ为中间变量，；T_L为负载转矩。

1.3 电动机参数在线辨识方法

电动机参数的准确性将影响孪生模型仿真结果，进而影响对电动机工况判断的准确性。为了避免电动机不同工况下参数时变带来的影响，孪生模型周期性地采用粒子群算法进行在线参数辨识。为便于计算，假设定、转子总电感相同，即L_ss=L_rr。

标准粒子群算法易陷入局部最优解，为有效控制粒子速度达到局部与全局搜索能力的平衡，本文采用基于压缩因子的改进粒子群算法^[20]计算电动机参数，待求参数为4维向量[R_s, R_r, L_ss, L_m]^T，粒子群的位置、速度更新公式如式（5）—式（6）所示：

(5)

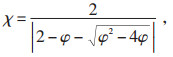
(6)

式中：v_id(k)、x_id(k) 分别为第d维搜索空间中第i粒子的第k次迭代的速度和位置；r₁、r₂是0与1之间的随机数；c₁、c₂分别为个体、群体加速因子；χ为压缩因子；φ为中间变量，φ=c₁+c₂；p_id(k)、p_gd(k) 分别为第d维第i个粒子与全体粒子的历史最优位置。

算法的适应度 F（即目标函数）为定子电流仿真与实测值的偏差，如式（7）所示：

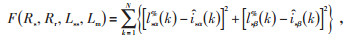
(7)

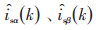
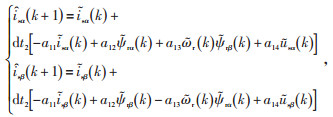
式中：N为数据个数；l_sα^%(k)、l_sβ^%(k) 为α、β轴第k步定子电流的实测值；为α、β轴第k步定子电流的计算值。电流的计算值由式（1）离散化可得，如式（8）所示。

(8)

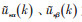
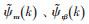
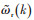
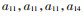
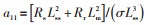
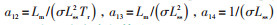
式中：dt₂为孪生模型仿真步长；为α、β轴第k步定子电压的实测值；为第k步α、β轴转子磁链实测值；为第k步转速实测值；为系数，，。

1.4 自适应变步长算法

为了缩短数字孪生系统的仿真耗时，实现与电动机的实时联合仿真，孪生模型采用自适应变步长算法。根据孪生模型与电动机实测值的偏差确定孪生模型仿真步长，如式（9）—式（11）所示。自适应变步长算法示意图如图 2所示。

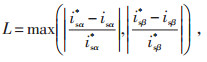
(9)

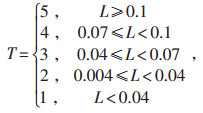
(10)

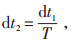
(11)

式中：L为状态变量的最大偏差；为α、β轴定子电流实测值；T为步长倍数；dt₁为电动机传感器测量步长。

1.5 电动机工况实用判别方法

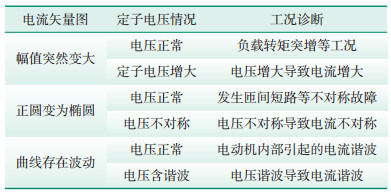
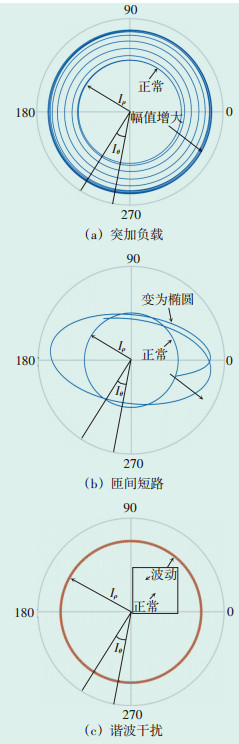
考虑到电动机定子电流比其他状态量更易测量，提出了基于电流空间矢量的电动机工况实用判别方法。通过对比孪生模型仿真电流矢量图与实测电流矢量图的幅值、不对称度等特征，能直观掌握电动机运行特性。电动机实用工况判断方法如 表 1所示。几种典型工况的电流矢量如图 3所示。

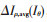
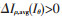
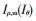
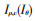
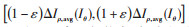
在此基础上，为了解决电动机正常运行时因传感器受干扰、电动机齿槽效应等因素导致电流矢量波动、电动机某些早期故障特征不明显的问题，数字孪生模型根据电动机以往运行数据自动记录前 H个周期内电流矢量实测与计算值的偏差 ，并引入偏差裕度ε（ε为接近零的正数），若 ，当电流实测值 与计算值 的偏差在 区间内时，认为电动机处于正常运行状态，如式（12）—式（13）所示。

当孪生仿真系统测量到一定程度的电流偏差时，即从备选故障（转子断条、匝间短路等）模型库中选择与实际最匹配的模型，从而识别故障。

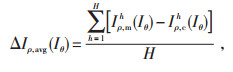
(12)

式中：H表示周期个数。

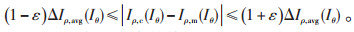
(13)

1.6 数字孪生仿真整体流程

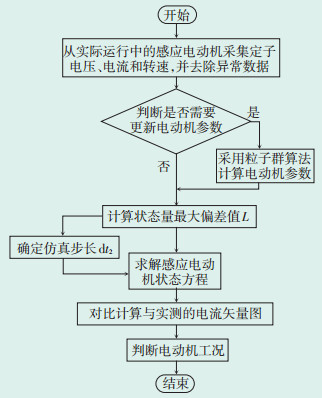
本文提出的数字孪生模型仿真流程如图 4所示。

具体包含以下步骤：

（1）由传感器测得电压、电流等数据，并删除异常数据。

（2）判断是否需要更新电动机参数。如需要，则采用粒子群算法计算电动机参数并更新。

（3）计算状态量仿真与计算值的最大偏差 L，并根据式（11）确定数字孪生仿真步长dt₂。

（4）求解感应电动机状态方程。

（5）结合电流矢量图与电动机工况实用判别方法，判断电动机运行状态。

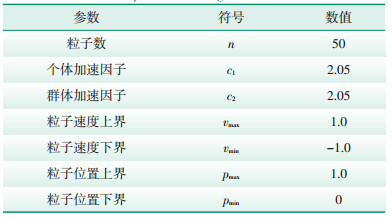
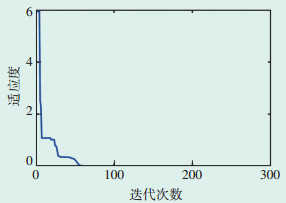
2 算例分析

为了验证数字孪生模型的实际效果，将其应用于某电厂辅机系统中的一台高压大功率感应电动机。首先运用基于压缩因子的改进粒子群算法辨识电动机参数，算法中采用的参数如表 2所示。迭代过程中适应度变化曲线如图 5所示。辨识得到的电动机参数如表 3所示，算法寻优总耗时6.87 s。

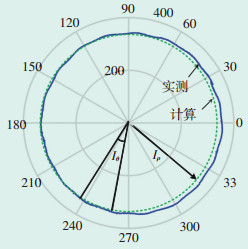
实测电流与孪生模型计算的电流矢量如图 6所示。传感器测量步长dt₁为250 μs。由图 6可知，计算所得电流矢量图为正圆，而实测电流矢量图偏离正圆。表明实际电动机的三相电流不完全对称，但偏离正圆的程度较小，故不认为其发生了不对称故障。此外，实测电流矢量图存在一定程度的波动，是由电动机本体导致的谐波引起的。

表 4对比了采用传统模型与数字孪生模型计算5 s稳态与暂态过程的仿真耗时，其中暂态过程以电动机突加负载为例。为确保仿真精度，传统模型的步长选定为50 μs；孪生模型根据自适应变步长算法自动调节步长。由表 4可知，当电动机稳态时，采用数字孪生模型的耗时相比传统模型缩短了2.90 s；暂态时，仿真耗时缩短了2.54 s。表明本文所提的自适应变步长方法在电动机不同工况下均能够有效缩短仿真耗时，提升了电动机状态监测的效率。

3 结论

本文针对电厂辅机系统中高压大功率电动机状态监测存在的问题，建立了感应电动机数字孪生模型，确立了实际电动机与虚拟电动机的数据交互方法，并通过电动机工况实用判断方法判断电动机运行状态。最后进行了实验验证，主要结论如下：

（1）所提出的自适应变步长算法根据仿真与实测值确定仿真步长，能有效缩短仿真耗时，满足状态监测的实时性要求。

（2）提出基于电流矢量的电动机工况实用判断方法，结合电压情况，能够区分出电动机稳定运行时的微小电流波动，并判断电动机是否存在不对称故障、突加负载等暂态工况。

（3）针对6 kV、1600 kW感应电动机进行实验验证，结果表明，本文提出的数字孪生系统在稳态、暂态仿真耗时分别缩短了2.90 s与2.54 s，且能准确判断电动机运行工况，体现了孪生模型的有效性。