2. 昆明理工大学 电力工程学院,昆明 650504;
3. 中国能源建设集团云南省电力设计院有限公司,昆明 650051
2. Kunming University of Science and Technology, Kunming 650504, China;
3. China Energy Engineering Group Yunnan Electric Power Design Institute Co., Ltd., Kunming 650051, China
近年来,随着社会经济的快速发展,电力负荷急剧增加,波动范围也逐渐增大,系统需要扩建设备来调节此类短期的负荷急剧波动,造成投资成本加大、设备使用率降低,如何实现深度调峰以解决负荷波动问题成为电力系统负荷规划亟需解决的难题之一[1-5]。
目前对电力负荷削峰填谷的研究主要集中于需求响应和储能系统参与调峰[6-8]。文献[9]采用马尔可夫决策过程反映用户用电状态与外部激励的不确定性,提出多时段耦合的实时激励,该激励策略能够引导用户积极合理地参与电网运行,有效实现削峰填谷。文献[10]针对家用能源局域网络中用户行为的不确定性,提出了一种基于时变价格的家电调度鲁棒优化模型,在目标函数中提出了鲁棒分散指数(Robust Scatter Index,RSI)的满意度水平反映用户行为造成的舒适度损失。文献[11-12]建立电池储能系统调峰、调频模型,考虑电池退化、运行约束以及客户负载和调节信号中的不确定性,提出了一种简单的阈值实时算法,相比之前储能系统的单一应用,联合优化模型既能有效抑制负荷与频率波动,又能保持良好的经济性。文献[13]将储能系统的填谷调度模型、削峰调度模型应用于风电高渗透电网的调峰场景中,该模型可以有效降低电网的负荷峰谷差,提高风电接纳量。
由上述研究文献可知,通过对资源使用时间的调度,需求响应和储能出力有类似的调峰效果。但目前大部分研究都是通过单一的需求响应或储能系统进行调峰,少有同时联合两者进行调峰的案例,虽然两种单一调峰策略对负荷调节能够起到至关重要的作用,但仍未实现资源利用最大化和经济性最优。因此,如何实现需求响应和储能系统的有效配合、实现资源最大利用是一个值得研究的方向。
本文提出一种考虑需求响应与储能系统联合调峰优化策略:首先,分析用户需求特性和负荷曲线趋势,分别建立了需求响应和储能系统调峰优化模型;然后,基于线性加权和法,构建了以用户购能成本和优化后负荷标准差最小为目标函数的联合调峰优化策略模型;最后,运用Matlab+Gurobi求解器进行算例模型求解。分析结果表明,建立联合调峰优化策略模型,可以有效降低负荷波动,提高用户的经济性。
1 考虑需求响应的调峰模型需求响应可以分为价格型需求响应和激励型需求响应,本文考虑较为常用的基于分时电价的价格型需求响应机制[14]。分时电价通过设定各时段不同的用电价格来引导用户改变用电行为[15],从而优化负荷曲线,达到减轻系统调峰压力或提高新能源消纳的目的。
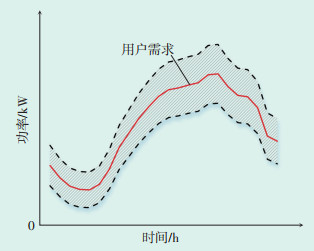
可转移负荷范围曲线如图 1所示,阴影部分为可转移负荷的调节范围,用户可根据分时电价调整自身用电需求,电价在引导用户需求转化的前期,用户进行响应的积极性较高,约10%的用户电量可参与积极响应。
|
| 图 1 可转移负荷范围曲线 Figure 1 Transferable load range curve |
根据上述原则,将日前负荷预测值进行分解,考虑负荷在时间尺度上的转移,将其划分为固定型负荷和可转移型负荷两部分,如式(1)所示:
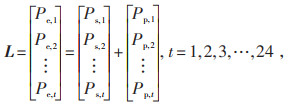
|
(1) |
式中:L为日前预测负荷;Pe, t为需求响应后电负荷t时段的值;Ps, t为电负荷t时段的固定型负荷即不参加需求响应的负荷;Pp, t为电负荷t时段的可转移型负荷即调度周期内可在不同时段间转移的负荷。
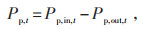
|
(2) |
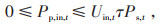
|
(3) |
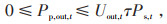
|
(4) |
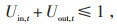
|
(5) |
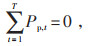
|
(6) |
式中:Uin, t、Uout, t为二进制变量,表示在t时段可转移型负荷的转入、转出状态;Pp, in, t、Pp, out, t为t时段可转移型负荷的转入、转出功率;τ为可转移负荷率。为不影响用户的用电量,保证用户的用能质量需求,可转移型负荷在一个调度周期内的总量不变,见式(6)。
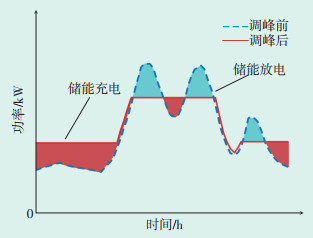
2 考虑储能系统的调峰模型储能系统可将需求侧管理规划中的高峰时段转移到非高峰时段,具体来讲,储能系统通过在非高峰时段电价较低时充电和在高峰时段电价较高时放电来参与调峰。储能系统参与调峰前、后对比如图 2所示。
|
| 图 2 储能系统参与调峰前后对比 Figure 2 Comparison diagram of energy storage system before and after peak shaving |
具体模型如下:
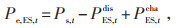
|
(7) |
式中:Pe, ES, t为储能系统参与出力后的电网负荷值;PES, tcha、PES, tdis为储能系统t时段的充、放电功率。
储能系统充、放电功率约束如下:
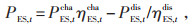
|
(8) |
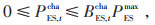
|
(9) |
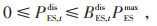
|
(10) |
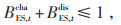
|
(11) |
式中:PES, t为t时段储能系统的输出功率;PESmax为储能系统的单次充、放电最大功率;BES, tcha、BES, tdis均为二进制变量,分别为储能系统t时段充、放状态参数;BES, tcha = 1,BES, tdis = 0表示处于充能状态;BES, tcha = 0,BES, tdis = 1表示处于放能状态;ηES, tcha、ηES, tdis分别为储能系统的充、放电效率。
储能系统剩余电量(State of Charge,SOC)约束如下:
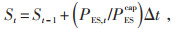
|
(12) |
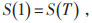
|
(13) |
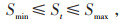
|
(14) |
式中:St为t时段储能系统的容量;Δt为1 h;PEScap为储能系统的额定容量;T为一个调度周期;Smax、Smin分别为储能系统容量的上、下限。式(13)表明储能系统一个周期内能量守恒。
3 考虑需求响应与储能系统的联合调峰优化策略模型 3.1 目标函数本文采用线性加权和法,以优化后的用户购能成本和负荷标准差最小为目标函数,如式(15)所示:
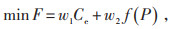
|
(15) |
式中:Ce为用户购电成本;f(P) 为优化后的负荷曲线负荷标准差;w1、w2分别为Ce和f(P) 的权重系数。
用户购电成本Ce为:
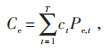
|
(16) |
式中:ct为t时刻电网向用户提供的分时电价。
优化后负荷曲线的负荷标准差f(P) 为:
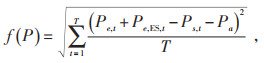
|
(17) |
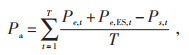
|
(18) |
式中:Pa为负荷曲线削峰填谷后的负荷平均值。
3.2 约束条件(1)联合调峰约束。需求响应与储能系统联合调峰约束条件为式(2)—式(6)、式(8)—式(14)。
(2)联合优化后功率平衡约束,见式(19):
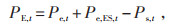
|
(19) |
式中:PE, t为经过需求响应和储能系统调峰联合优化后的电网负荷功率。
3.3 评价指标采用削峰填谷算法模型对负荷曲线进行优化后,对优化前、后的负荷曲线进行对比,通过评价标准来衡量模型的优劣[16]。常见的评价标准如下。
(1)绝对峰谷差ΔP,见式(20):
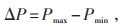
|
(20) |
式中:Pmax、Pmin分别为经过需求响应和储能联合调峰后的负荷峰值和谷值。ΔP越小,表明负荷偏差越小。
(2)峰谷系数β,见式(21):
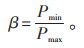
|
(21) |
峰谷系数β为负荷曲线的谷值和峰值比,β越大,表明优化效果越好。
(3)峰谷差率Ψ,见式(22):
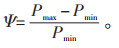
|
(22) |
峰谷差率Ψ表征负荷曲线的波动程度,Ψ越小,表明优化效果越好。
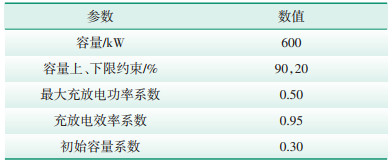
4 算例分析以我国南方某商业园区为例,该园区典型日负荷数据参考文献[17],电负荷高峰分别出现在10:00和20:00。参与需求响应的分时电价见表 1[17]。储能系统参数见表 2[18]。假定可转移电负荷率为10%,既考虑提高用户参与电网互动的积极性,又兼顾减小电网负荷波动提高的安全性,实现电网与用户双赢的基础上,设权重系数w1、w2均为0.5,上述模型为混合整数线性模型(MILP),采用Matlab R2021a仿真平台,外接YALMIP工具箱调用优化求解器Gurobi 9.1.2进行求解。
| 表 1 分时电价 Table 1 Time-of-use electricity price |
| 表 2 储能系统参数 Table 2 Parameters of energy storage system |
为验证考虑需求响应与储能系统的联合调峰优化策略模型的有效性,本文设置以下4种场景进行对比分析。
(1)场景1:不考虑需求响应和储能系统参与调峰;
(2)场景2:不考虑储能系统,仅考虑需求响应参与调峰;
(3)场景3:不考虑需求响应,仅考虑储能系统参与调峰;
(4)场景4:既考虑需求响应,又考虑储能系统参与调峰。
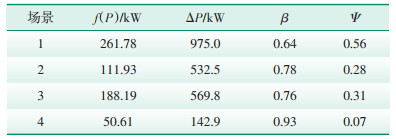
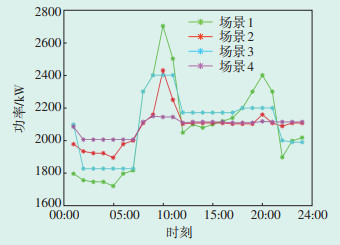
不同场景优化结果见图 3、表 3,可以看出,场景1在未经过需求响应和储能系统的优化的情况下,负荷波动最大,负荷曲线标准差最大为261.78 kW,绝对峰谷差最大为975 kW,峰谷系数最小为0.64,峰谷差率最大为0.56;场景4经过需求响应和储能系统的联合调峰优化后,负荷波动最小,负荷曲线标准差最大为50.61 kW,绝对峰谷差最大为142.9 kW,峰谷系数最小为0.93,峰谷差率最大为0.07;场景2、3分别经过需求响应和储能系统优化后,电网负荷都较场景1得到了一定的优化,场景2的各优化指标都比场景3具有优势,说明需求响应的优化效果更好。
|
| 图 3 4种场景的电网负荷优化曲线 Figure 3 Grid load optimization curves for four scenarios |
| 表 3 4种场景的评价指标结果 Table 3 Evaluation index results of four scenarios |
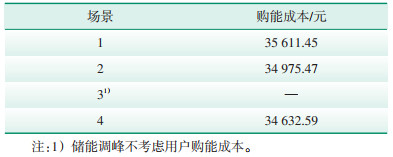
各场景成本如表 4所示。由表 4可以看出,经需求响应优化后,场景2较场景1购能成本降低了635.98元;经需求响应和储能系统联合调峰优化后,场景4较场景2购能成本降低了342.88元,较场景1购能成本降低了978.86元。相比于考虑单一的需求响应调峰优化,需求响应和储能系统联合调峰优化策略能够充分利用可调度资源使购能成本最低,实现经济效益最大化。
| 表 4 4种场景的购能成本 Table 4 Energy purchase cost of four scenarios |
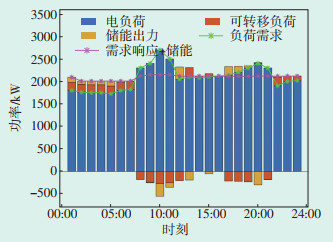
经需求响应和储能系统联合调峰优化后,各设备出力如图 4所示。由图 4可以看出,01:00—08:00电价谷值时段,商业用户增加自身用电量且值为各时刻最大可转移负荷量,此时储能系统根据电价需求进行充电,充电至容量最大;在10:00—13:00、17:00— 20:00电价峰值时段,商业用户减少自身用电量,储能系统进行放电,在20:00负荷峰值时最大放电,起到削峰的作用;在其他时段,用户和储能系统根据自身需要和负荷波动进行少量的负荷转移和充放电。由两条曲线的负荷趋势验证了联合调峰优化策略实现削峰填谷的有效性。
|
| 图 4 联合调峰优化后的各单元出力 Figure 4 Output diagram of each unit after joint peak shaving optimization |
本文提出了一种考虑需求响应和储能系统出力的联合调峰优化策略模型,为了使负荷曲线的调峰效果达到最优,分别建立了需求响应调峰模型、储能系统出力调峰模型以及两者联合调峰模型,并通过相应的评价指标对调度策略进行了评估,得到以下结论。
(1)相较于考虑单一的需求响应调峰和储能系统出力调峰,联合调峰优化策略使各项评价指标均达到优化,说明该优化策略能够有效平抑负荷波动,平滑负荷曲线。
(2)相较于优化前和经过需求响应调峰优化后的购能成本达到了降低,证明联合调峰优化策略能够充分利用可调度资源使购能成本最低,实现经济效益最大化。
在新能源并网装机容量不断增加、负荷不断增大的情况下,本文所提的联合调峰优化策略有助于降低电网负荷波动,提高电网稳定性。但是文中尚未考虑储能系统自身的成本函数,成本过高会导致其不参与调峰,因此后续可以进一步开展考虑储能系统的成本函数对调峰策略的影响研究。
| [1] |
陈爱博, 王存旭. 需求响应对电力市场的效益影响研究综述[J].
沈阳工程学院学报(自然科学版), 2019, 15(4): 338-342 CHEN Aibo, WANG Cunxu. Review on the effect of demand response on power market efficiency[J]. Journal of Shenyang Institute of Engineering(Natural Science), 2019, 15(4): 338-342 (  0) 0)
|
| [2] |
胡朝阳, 毕晓亮, 王珂, 等. 促进负备用跨省调剂的华东电力调峰辅助服务市场设计[J].
电力系统自动化, 2019, 43(5): 175-182 HU Zhaoyang, BI Xiaoliang, WANG Ke, et al. Design of peak regulation auxiliary service market for East China Power Grid to promote inter-provincial sharing of negative reserve[J]. Automation of Electric Power Systems, 2019, 43(5): 175-182 (  0) 0)
|
| [3] |
黄园芳, 刘云凯, 郑世明, 等. 计及负荷不确定性的配电变压器重过载风险预警[J].
电网与清洁能源, 2021, 37(10): 17-24 HUANG Yuanfang, LIU Yunkai, ZHENG Shiming, et al. Heavy overload risk early warning of distribution transformers considering load uncertainty[J]. Advances of Power System & Hydroelectric Engineering, 2021, 37(10): 17-24 (  0) 0)
|
| [4] |
贾志军, 李强, 李柏利. 京津唐电网火电机组深度调峰经济性分析[J].
内蒙古电力技术, 2018, 36(1): 7-10 JIA Zhijun, LI Qiang, LI Baili. Economic analysis on deep peak shaving of thermal power unit in Beijing-Tianjin-Tangshan Power Grid[J]. Inner Mongolia Electric Power, 2018, 36(1): 7-10 (  0) 0)
|
| [5] |
马可心, 陈晓利, 宋浩, 等. 300 MW级供热机组多模式深度调峰协同运行技术路线研究[J].
东北电力技术, 2021, 42(11): 5-7 MA Kexin, CHEN Xiaoli, SONG Hao, et al. Study on technical route of multi-mode deep peak-shaving cooperative operation for 300 MW heating units[J]. Northeast Electric Power Technology, 2021, 42(11): 5-7 (  0) 0)
|
| [6] |
陈艳波, 武超, 焦洋, 等. 考虑需求响应与储能寿命模型的火储协调优化运行策略[J].
电力自动化设备, 2022, 42(2): 16-24 CHEN Yanbo, WU Chao, JIAO Yang, et al. Coordinated optimal operation strategy of thermal power-energy storage considering demand response and life model of energy storage[J]. Electric Power Automation Equipment, 2022, 42(2): 16-24 (  0) 0)
|
| [7] |
李建林, 马会萌, 袁晓冬, 等. 规模化分布式储能的关键应用技术研究综述[J].
电网技术, 2017, 41(10): 3365-3375 LI Jianlin, MA Huimeng, YUAN Xiaodong, et al. Overview on key applied technologies of large-scale distributed energy storage[J]. Power System Technology, 2017, 41(10): 3365-3375 (  0) 0)
|
| [8] |
Wang S., Bi S., Zhang Y.. Demand Response Management for Profit Maximizing Energy Loads in Real-Time Electricity Market[J].
IEEE Transactions on Power Systems, 2018, 33(6): 6387-6396 DOI:10.1109/TPWRS.2018.2827401 (  0) 0)
|
| [9] |
张全明, 崔晓昱, 张笑弟, 等. 计及用户不确定性的多时段耦合需求响应激励优化策略[J/OL]. 中国电机工程学报: 1-11[2022-05-10]. http://kns.cnki.net/kcms/detail/11.2107.TM.20220302.1738.005.html.
ZHANG Quanming, CUI Xiaoyu, ZHANG Xiaodi, et al. Multi-period coupling demand response incentive optimization strategy considering user uncertainty[J/OL]. Proceedings of the CSEE: 1-11[2022-05-10]. http://kns.cnki.net/kcms/detail/11.2107.TM.20220302.1738.005.html. (  0) 0)
|
| [10] |
Ran X., Liu K.. Robust Scatter Index Method for the Appliances Scheduling of Home Energy Local Network With User Behavior Uncertainty[J].
IEEE Transactions on Industrial Informatics, 2019, 15(7): 4129-4139 DOI:10.1109/TII.2019.2897126 (  0) 0)
|
| [11] |
Shi Y., Xu B., Wang D., et al. Using battery storage for peak shaving and frequency regulation: joint optimization for superlinear gains[J].
IEEE Transactions on Power Systems, 2018, 33(3): 2882-2894 (  0) 0)
|
| [12] |
Liu D, Jin Z, Chen H, et al. Peak Shaving and Frequency Regulation Coordinated Output Optimization Based on Improving Economy of Energy Storage[J].
Electronics, 2022, 11(1): 29 (  0) 0)
|
| [13] |
李军徽, 张嘉辉, 穆钢, 等. 计及负荷峰谷特性的储能调峰日前优化调度策略[J].
电力自动化设备, 2020, 40(7)128-133, 140 LI Junhui, ZHANG Jiahui, MU Gang, et al. Day-ahead optimal scheduling strategy of peak regulation for energy storage considering peak and valley characteristics of load[J]. Electric Power Automation Equipment, 2020, 40(7)128-133, 140 (  0) 0)
|
| [14] |
王守相, 张善涛, 王凯, 等. 计及分时电价下用户需求响应的分布式储能多目标优化运行[J].
电力自动化设备, 2020, 40(1): 125-132 WANG Shouxiang, ZHANG Shantao, WANG Kai, et al. Multi-objective optimal operation of distributed energy storage considering user demand response under time-of-use price[J]. Electric Power Automation Equipment, 2020, 40(1): 125-132 (  0) 0)
|
| [15] |
周正威. 基于"负荷-电价"联动的热电联产系统弃风消纳研究[D]. 宜昌: 三峡大学, 2019.
(  0) 0)
|
| [16] |
谢彬. 基于电力用户用电行为的配电网削峰填谷评估方法研究[D]. 北京: 北京邮电大学, 2021.
(  0) 0)
|
| [17] |
魏震波, 马新如, 郭毅, 等. 碳交易机制下考虑需求响应的综合能源系统优化运行[J].
电力建设, 2022, 43(1): 1-9 WEI Zhenbo, MA Xinru, GUO Yi, et al. Optimal operation of integrated energy system considering demand response under carbon trading mechanism[J]. Electric Power Construction, 2022, 43(1): 1-9 (  0) 0)
|
| [18] |
陈锦鹏, 胡志坚, 陈嘉滨, 等. 考虑阶梯式碳交易与供需灵活双响应的综合能源系统优化调度[J].
高电压技术, 2021, 47(9): 3094-3104 CHEN Jinpeng, HU Zhijian, CHEN Jiabin, et al. Optimal dispatch of integrated energy system considering ladder-type carbon trading and flexible double response of supply and demand[J]. High Voltage Engineering, 2021, 47(9): 3094-3104 (  0) 0)
|
 2022, Vol. 40
2022, Vol. 40