2. 江苏金智科技股份有限公司, 南京 211106
2. Jiangsu Jinzhi Technology Co., Ltd., Nanjing 211106, China
现阶段我国能源紧缺、环境污染问题突出,风电、光伏因其环境友好、成本低且可再生得到了广泛应用。工业微电网已成为提高可再生能源利用率的主要方式之一,其储能系统可通过削峰填谷、需量管理、调峰辅助服务等渠道来减少用户用电成本,获取一定的经济效益。但由于预测技术的局限,很难准确获得实际光伏、风电出力和负荷的大小,其随机性严重影响了微电网的安全、稳定和经济运行。在此背景下,研究计及可再生能源出力和负荷随机性的微电网优化调度问题具有重要意义。
经济优化调度模块是微电网能量管理系统的重要组成部分,目前,基于确定性方法的经济优化调度技术已有丰富的研究成果。文献[1]针对光储微电网,考虑用电舒适度和经济性,以用户满意度为目标建立日前调度模型。文献[2]综合用户侧储能规划和优化,提出一种计及需量管理和分时电价的工业大用户储能评估及优化调度方法。文献[3] 建立了考虑微源提供有功和无功出力,并计及制热收益的热电联产型微网系统多目标经济调度模型,基于最大模糊满意度法将其转换为单目标优化问题,并采用改进遗传算法进行求解。文献[4]针对微电网能量管理实际情况,建立基于储能水平控制的户用微电网日前用电计划调度模型,并基于混合编码方式和遗传算法进行优化模型的求解。
上述研究中,均假定注入功率与预测值相等,没有考虑其随机性。但在实际中,风电、光伏出力和负荷大小的波动性很难避免。当前,计及随机性的建模方法有基于场景的随机规划和机会约束规划等。文献[5-6]考虑风电出力的随机性,以日前调度经济运行为目标,采用场景法来提高微电网适应风电出力随机性的灵活性。然而,该类方法随机因素和场景量多,计算量大,且难以准确获得概率分布函数。文献[7]考虑了风能和光伏的波动性及相互间的互补性,建立基于机会约束规划的微电网随机优化模型,但其求解方法依赖于分布函数的描述,且当随机变量服从较复杂的函数时,数学上一般非凸,计算过程复杂,很难获得全局最优解。
信息间隙决策理论(Information Gap Decision Theory,IGDT)由美国学者Ben-Haim于2001年提出[8],它不需要随机变量的任何概率分布假设,注重已知信息与未知信息之间的间隙。该理论定义了不确定环境下的决策性能函数,有效解决了不确定变量的随机性描述和评价准则选取两个问题。IGDT已在机组组合策略的优化[9-10]、含风电电网的调度[11]以及电网负荷恢复优化策略[12-13]等领域得到广泛应用,然而,在工业园区微电网日前优化调度方面的应用还有待研究。
本文针对含光伏系统、储能系统和负荷的并网型工业微电网,考虑峰谷分时电价和需量管理,以工业园区日电费成本最小为目标函数,建立需量管理捆绑峰谷套利的微电网日前优化调度模型。在此基础上,基于IGDT提出计及光伏出力和负荷随机性的微电网多目标鲁棒优化调度模型,制订鲁棒决策方案,研究不同预设成本与随机变量波动区间的关系。
1 微电网优化调度模型 1.1 目标函数从经济角度出发,目标是使工业园区的日电费最小,其优化时间尺度为1 h,表达式为:
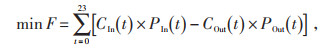
|
(1) |
式中:F为工业园区的日电费;CIn(t)和COut(t)分别为在t至t + 1时段园区买入电量电价和卖出电量电价;PIn(t)和POut(t)分别为在t至t + 1时段流入园区和流入电网的有功功率。
1.2 约束条件 1.2.1 园区功率平衡方程园区功率平衡方程见式(2):
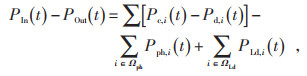
|
(2) |
式中:Pc, i(t)和Pd, i(t)分别为储能系统在t至t + 1时段的充电功率和放电功率;Pph, i(t)和PLd, i(t)分别为t至t + 1时段光伏系统的出力大小和负荷大小;Ωbs、Ωph和ΩLd表示储能系统、光伏系统和负荷集合。
1.2.2 储能系统运行功率约束储能系统在同一时刻不能既充电又放电,须在约束条件中考虑这一特性。同时,储能系统任意时刻的充放电功率均不能大于其最大的充放电功率,其约束由式(3)表示:
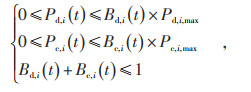
|
(3) |
式中:Bd, i(t)和Bc, i(t)为取值为0或1的变量,分别表示储能系统在t时段的放电和充电状态,Bd, i(t) 为1表示储能系统处于放电状态,Bc, i(t)为1表示储能系统处于充电状态,若均为0,则表示储能系统处于停止状态,既不充电也不放电;Pd, i, max和Pc, i, max分别为储能系统的最大放电功率和最大充电功率。
1.2.3 关口功率约束类似储能系统,关口功率在同一时刻也不能既从电网买电又反送给电网功率,其约束由式(4)表示:
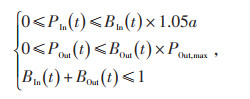
|
(4) |
式中:BIn(t)和BOut(t)为取值为0或1的变量,分别表示园区在t时段从电网买电和反向送电的状态,BIn(t)为1表示园区从电网买电状态,BOut(t)为1表示园区向电网送电状态,若均为0则表示园区既不从电网买电也不反向送电;POut, max为工业园区反送给电网有功功率的最大值,目的是降低工业园区反送功率对大电网安全性和稳定性的影响;a为需量核定值,即工业用户上报的最大需量值,通常工业园区实际最大需量超过1.05a时,其超过部分将以加收一倍的方式进行惩罚。
1.2.4 储能系统荷电状态约束储能系统荷电状态由式(5)表示:
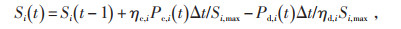
|
(5) |
式中:Si(t)为储能系统在t时刻的荷电状态;Si, max为储能系统的最大荷电状态;ηc, i和ηd, i分别为储能系统的充电效率和放电效率;Δt为时间差。
此外,储能系统日前优化调度具有周期性特征,增加如下约束,使其在每个调度周期的始末时刻储能系统荷电状态相等[14-15],即:
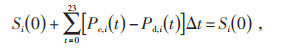
|
(6) |
式中:Si(0)为储能系统初始荷电状态,该式表示储能系统在一个调度周期内的充电量和放电量之和为零。
2 基于IGDT的多目标鲁棒优化调度 2.1 IGDT概述IGDT是一种处理不确定性的非概率且非模糊的优化方法,它是在满足预设目标可接受范围的前提下,研究不确定参数所造成的可能影响[8]。考虑如下优化模型:
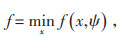
|
(7) |
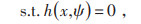
|
(8) |
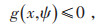
|
(9) |
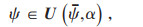
|
(10) |
式中:f为目标函数;x为决策变量;ψ为不确定参数;h为等式约束;g为不等式约束;U为不确定参数所属的集合;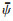
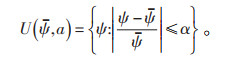
|
(11) |
当ψ与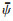
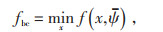
|
(12) |
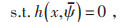
|
(13) |
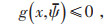
|
(14) |
式中:fbc为不确定参数的实际值与预测值相等时的最优值,设为基准值。
对于保守的决策者而言,建立鲁棒决策模型,设定不高于基准值的目标函数阈值,并以偏差系数最大为优化目标,优化计算获得一组鲁棒解,具体表达为:
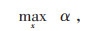
|
(15) |
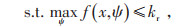
|
(16) |
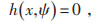
|
(17) |
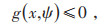
|
(18) |
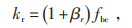
|
(19) |
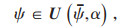
|
(20) |
式中:kr—目标函数的阈值;
βr—风险规避系数。
2.2 多目标鲁棒优化调度模型文中选取光伏系统有功出力和负荷为不确定参数,根据式(11),其波动范围可表示为:
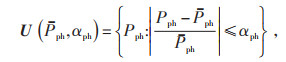
|
(21) |
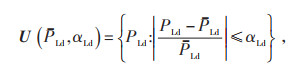
|
(22) |
式中: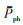
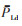
在模型(15)—(20)中,当实际光伏有功出力低于预测值和负荷高于预测值时,所需的日电费成本最大。此时,除约束条件式(2)—(6)外,基于IGDT计及光伏出力和负荷随机性的微电网多目标鲁棒决策模型如下:
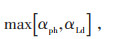
|
(23) |
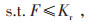
|
(24) |
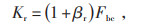
|
(25) |
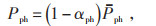
|
(26) |
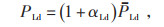
|
(27) |
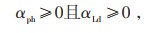
|
(28) |
式中:Kr为预设成本;βr为偏差因子;Fbc为光伏有功出力和负荷等于预测值时的电费成本。
2.3 模型求解方法求解多目标问题的方法有多种,如线性加权求和法、ε-约束法和智能优化算法等[16],本文采用ε-约束法来求解基于IGDT的多目标鲁棒决策模型。除约束条件式(2)—(6),式(23)—(28)外,其转化后的单目标模型为:
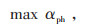
|
(29) |
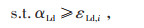
|
(30) |
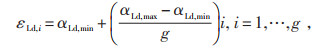
|
(31) |
式中:αLd, max和αLd, min分别为子目标函数αLd独自作用下的最大值和最小值;εLd, i为αLd的第i个阈值取值;g为等间距网格点数。
综上,式(29)—(31)和约束条件式(2)—(6)、(24)—(28)为混合整数线性规划模型,文中采用Python MIP工具包进行模型求解,计算αLd各个阈值下的优化子问题,以获得Pareto最优解集。在获得最优解集后,采用模糊满意度函数理论来确定解集中的折中解。定义的模糊满意度函数如下:
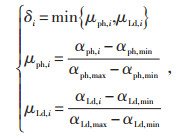
|
(32) |
式中:δi为Pareto解集中第i个解的模糊满意度函数值;αph, max和αph, min分别为αph的最大值和最小值;μLd, i和μph, i分别为αph和αLd的标准满意度函数值,其值越接近于1,表明对该解越满意。通过式(32) 计算模糊满意度函数值后,选取δi最大的解作为折中解。
3 算例分析采用本文提出的多目标鲁棒优化调度模型和算法对某工业园区光储微电网进行仿真分析,以验证其有效性和合理性。仿真环境采用Windows 7 64位操作系统,内存4G,4核CPU,2.1 GHz主频。微电网系统包括一个光伏发电系统、一个储能系统和负荷。储能系统额定容量为500 kWh,充放电最大功率约束为65 kW,充放电效率均为0.9,荷电初始值为10%。需量核定值为1000 kW,倒送给电网的功率不设限。分时电价信息:峰时段为08:00—12:00和17:00—21:00,谷时段为00:00—08:00,平时段为12:00—17:00和21:00—24:00。峰谷平时段的买入电量电价分别为1.176元/kWh、0.335元/kWh和0.705元/kWh,工业园区的电量上网电价不分峰谷平时段,均为0.370元/kWh。
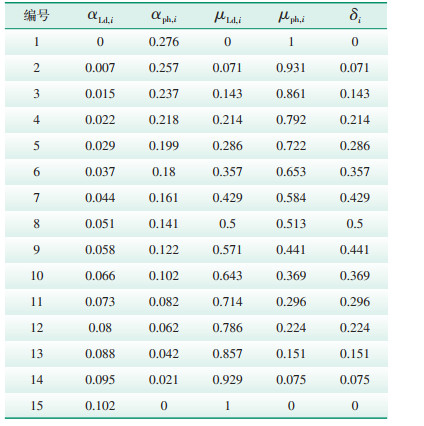
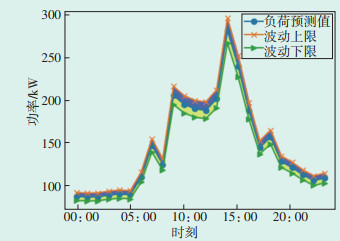
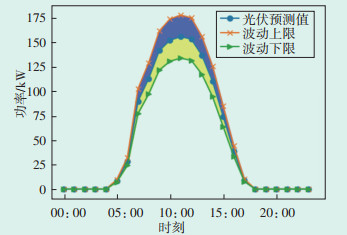
3.1 多目标鲁棒优化调度结果分析不考虑光伏系统出力和负荷的随机性时,其日电费成本为1 282.992元。当取偏差因子为0.2,即日电费预设成本为1 539.590元,等间距网格点数为15时,求得的帕累托解集如表 1所示。从表 1可以看出,当编号为1,即仅考虑光伏系统出力的不确定时,波动半径为0.276。当编号为15,即仅考虑负荷大小的不确定时,波动半径为0.102。当编号为8,模糊满意度函数值最大,为0.5,属于折中解,对应的光伏系统出力的波动区间为0.141,负荷大小的波动区间为0.051。图 1和图 2给出了折中解下光伏系统出力和负荷大小波动区间示意图。也就是说,无论光伏系统出力和负荷大小的实际值为多少,只要在图 1、图 2所示的波动区间范围内,其实际的电费成本均不会大于预设成本,此时储能系统的充放电策略具有鲁棒性,属于风险规避策略。
| 表 1 帕累托解集 Table 1 Pareto solution set |
|
| 图 1 负荷波动区间 Figure 1 Load fluctuation range |
|
| 图 2 光伏出力波动区间 Figure 2 Fluctuation range of PV output |
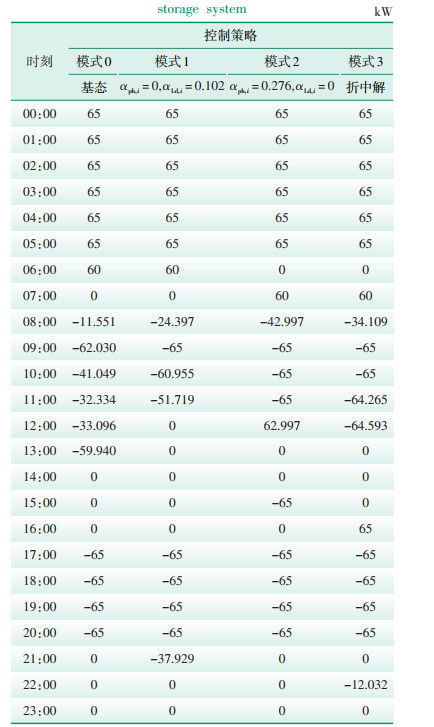
表 2给出了四种控制模式下储能系统的充放电策略。模式0为基态,即在不考虑随机性的情况下储能系统的充放电策略,模式1、模式2和模式3分别为仅考虑负荷波动性、仅考虑光伏系统出力波动性以及同时考虑光伏系统出力波动性和负荷波动性的折中解时的充放电策略。从表 2可以看出,四种模式下在00:00—08:00时段间多为充电策略且均达到了储能系统充电功率的上限,因为该时段为谷时段,其电价最低,所存储的能量可为峰时段供电。在17:00—21:00峰时段,四种模式均在放电且功率相同。其不同之处主要在于08:00—12:00峰时段和12:00—17:00平时段的充放电策略及其大小。
| 表 2 储能系统充放电策略 Table 2 Charge and discharge strategy of energy storage system |
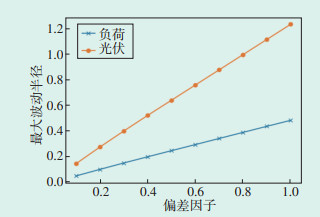
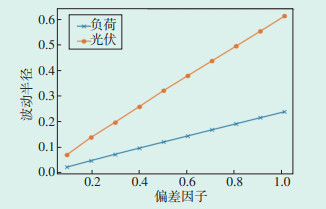
在3.1的基础上,给定不同的电费偏差因子可以获得波动区间与预设成本的关系。图 3给出了仅考虑光伏随机性和仅考虑负荷随机性时最大波动半径与偏差因子的关系,图 4为同时考虑光伏和负荷随机性时折中解的波动半径与偏差因子的关系图。从图 3、图 4可以看出,两者近似呈线性关系,即随着预设成本的增加,其应对光伏和负荷的不确定性也随之增强。
|
| 图 3 最大波动半径与偏差因子关系图 Figure 3 Relationship between maximum fluctuation radius and deviation factor |
|
| 图 4 折中解的波动半径与偏差因子关系图 Figure 4 Relationship between fluctuation radius and deviation factor of compromise solution |
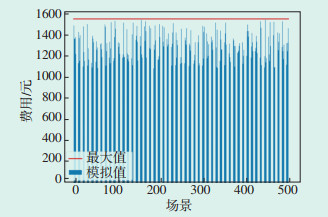
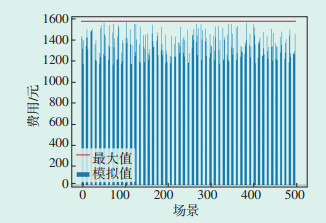
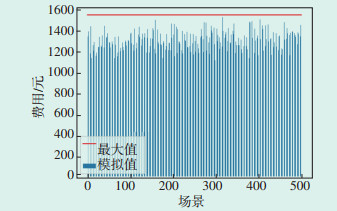
蒙特卡洛法又称随机抽样或统计试验方法,是将概率现象作为研究对象的数值模拟方法。为验证3.1节所述储能系统充放电策略的鲁棒性,基于蒙特卡洛法分别针对模式1、模式2和模式3进行模拟抽样试验,抽样数分别为500、500、1000。图 5、图 6、图 7分别为三种模式下的模拟结果,可以看出,各抽样样本的实际成本均不大于预设电费成本,其样本的平均成本分别为1 293.925元、1 309.871元以及1 309.124元,与预设成本1 539.590元差距较大,验证了基于IGDT获得的储能充放电策略对光伏、负荷的不确定性具有鲁棒性。
|
| 图 5 模式1下电费成本分布图 Figure 5 Distribution of electricity cost under mode one |
|
| 图 6 模式2下电费成本分布图 Figure 6 Distribution of electricity cost under mode two |
|
| 图 7 模式3下电费成本分布图 Figure 7 Distribution of electricity cost under mode three |
本文针对并网型光储微电网,计及光伏出力和负荷的波动性,提出基于IGDT的微电网多目标鲁棒优化调度模型和求解方法。通过实际数据仿真分析,结果表明:
(1) 与蒙特卡洛法对比分析,基于IGDT所得到的储能充放电策略能够保证实际光伏出力和负荷大小在其波动区间内时,所需要的电费成本不会超过预设电费成本,可为决策者提供风险规避策略。
(2) 利用ε-约束方法能有效刻画多目标问题的Pareto有效前沿,并运用模糊满意度理论确定Pareto解集中的折中解,为运行人员提供合理的鲁棒决策方案。
(3) 光伏出力和负荷的波动半径与预设电费成本具有近似线性相关关系,即随着可接受成本的增加其控制策略所允许的波动程度也更大。
文中主要是对光储微电网进行建模分析,较为简单,后续有必要针对更为复杂的微电网系统进行建模分析,并结合电力辅助服务市场,开展相关模型和鲁棒决策方案的研究。
| [1] |
曹金声, 曾君, 刘俊峰, 等. 考虑极限场景的并网型微电网分布鲁棒优化方法[J].
电力系统自动化, 2022, 46(7): 50-59 CAO Jinsheng, ZENG Jun, LIU Junfeng, et al. Distributionally Robust Optimization Method for Grid-connected Microgrid Considering Extreme Scenarios[J]. Automation of Electric Power Systems, 2022, 46(7): 50-59 (  0) 0)
|
| [2] |
陈丽娟, 吴甜恬, 柳惠波, 等. 基于需量管理的两阶段大用户储能优化模型[J].
电力系统自动化, 2019, 43(1): 194-200 CHEN Lijuan, WU Tiantian, LIU Huibo, et al. Demand management based two-stage optimal storage model for large users[J]. Automation of Electric Power Systems, 2019, 43(1): 194-200 (  0) 0)
|
| [3] |
马天祥, 贾伯岩, 张智远, 等. 基于二层规划的能源互联微电网能量优化调度方法[J].
电力系统自动化, 2019, 43(16): 34-43 MA Tianxiang, JIA Boyan, ZHANG Zhiyuan, et al. Energy Optimal Dispatching Method of Micro-energy Internet Based on Bi-level programming[J]. Automation of Electric Power Systems, 2019, 43(16): 34-43 (  0) 0)
|
| [4] |
侯慧, 薛梦雅, 陈国炎, 等. 计及电动汽车充放电的微电网多目标分级经济调度[J].
电力系统自动化, 2019, 43(17): 55-62 HOU Hui, XUE Mengya, CHEN Guoyan, et al. Multi-objective hierarchical economic dispatch for microgrid considering charging and discharging of electric vehicles[J]. Automation of Electric Power Systems, 2019, 43(17): 55-62 (  0) 0)
|
| [5] |
刘春晖, 张政, 牟辉龙, 等. 考虑不同场景的微电网短期经济调度分析[J].
电子器件, 2021, 44(6): 1491-1498 LIU Chunhui, ZHANG Zheng, MOU Huilong, et al. Analysis of Short-Term Economic Dispatch of Microgrid Considering Different Scenarios[J]. Chinese Journal of Electron Devices, 2021, 44(6): 1491-1498 DOI:10.3969/j.issn.1005-9490.2021.06.034 (  0) 0)
|
| [6] |
晏开封, 张靖, 何宇, 等. 基于机会约束的微电网混合整数规划优化调度[J].
电力科学与工程, 2021, 37(2): 17-24 YAN Kaifeng, ZHANG Jing, HE Yu, et al. The Optimal Dispatching of Mixed Integer Programming Based on Opportunity Constraint of Microgrid[J]. Electric Power Science and Engineering, 2021, 37(2): 17-24 (  0) 0)
|
| [7] |
Ben-Haim Y.
Information Gap decision theory[M]. San Di ego: Academic Press Inc, 2001: 317-346.
(  0) 0)
|
| [8] |
AHMADI A, ESMAEEL NEZHAD A, HREDZAK B. Security-constrained unit commitment in presence of lithium-ion battery storage units using information-gap decision theory[J].
IEEE Transactions on Industrial Informatics, 2019, 15(1): 148-157 (  0) 0)
|
| [9] |
汪超群, 韦化, 吴思缘. 基于信息间隙决策理论的多源联合优化机组组合[J].
中国电机工程学报, 2018, 38(12): 3431-3440 WANG Chaoqun, WEI Hua, WU Siyuan. Multi-power combined unit commitment based on information gap decision theory[J]. Proceedings of the CSEE, 2018, 38(12): 3431-3440 (  0) 0)
|
| [10] |
马欢, 刘玉田. 基于IGDT鲁棒模型的风电爬坡事件协调调度决策[J].
中国电机工程学报, 2016, 36(17): 4580-4588 MA Huan, LIU Yutian. IGDT robust model-based coordinated scheduling strategy for wind power ramp events[J]. Proceedings of the CSEE, 2016, 36(17): 4580-4588 (  0) 0)
|
| [11] |
赵奇, 吕洋, 王毅, 等. 考虑微电网灵活调节潜力的主动配电网鲁棒优化[J].
浙江电力, 2022, 41(1): 55-63 ZHAO Qi, LYU Yang, WANG Yi, et al. Robust Optimization of Active Distribution Networks Considering the Flexible Regulation Potential of Microgrids[J]. Zhejiang Electric Power, 2022, 41(1): 55-63 (  0) 0)
|
| [12] |
宋坤隆, 谢云云, 陈晞, 等. 基于信息间隙决策理论的电网负荷恢复鲁棒优化[J].
电力系统自动化, 2017, 41(15): 113-120 SONG Kunlong, XIE Yunyun, CHEN Xi, et al. Robust restoration method for power system load based on information gap decision theory[J]. Automation of Electric Power Systems, 2017, 41(15): 113-120 (  0) 0)
|
| [13] |
蔡紫婷, 彭敏放, 沈美娥. 考虑需求侧资源的智能小区综合能源日前优化调度[J].
电力自动化设备, 2021, 41(3)18-24, 32 CAI Ziting, PENG Minfang, SHEN Mei'e. Day-ahead optimal scheduling of integrated energy in smart communities considering demand side resources[J]. Electric Power Automation Equipment, 2021, 41(3)18-24, 32 (  0) 0)
|
| [14] |
冯其芝, 喻洁, 李扬, 等. 考虑分时电价的虚拟发电厂调度策略[J].
电力需求侧管理, 2014, 16(4): 1-5 FENG Qizhi, YU Jie, LI Yang, et al. Scheduling strategy of virtual power plant considering time-of-use power price[J]. Power Demand Side Management, 2014, 16(4): 1-5 (  0) 0)
|
| [15] |
Deb K.
Multiobjective, optimization using evolutionary algorithms[M]. New York: John Wiley & Sons, 2001.
(  0) 0)
|
 2022, Vol. 40
2022, Vol. 40