2. 三峡大学电气与新能源学院, 湖北 宜昌 443000
2. College of Electrical and New Energy, Three Gorges University, Yichang 443000, China
随着能源危机的出现和人们环保意识的提高,调整能源结构和推进分布式电源(Distributed Generation,DG)发展成为我国实现“碳中和”目标的重要举措[1-3]。在此背景下,集成了大量可调度单元的主动配电网(Active Distribution Network,ADN)应运而生。ADN管理和控制方式灵活,有助于DG消纳[4-6]。因此,对ADN系统的经济优化调度问题进行研究,对于降低ADN系统运行成本和提高清洁能源利用率具有重要意义[7-9]。
近年来,国内外专家学者对ADN经济优化调度方法进行了大量研究。文献[10]以配电网运行成本最小为上层目标函数,以购电成本和储能运行成本最小为下层目标函数,建立了ADN分层经济优化调度模型,采用交替方向乘子法将模型分解为上下两层进行求解,获得了最优调度方案。文献[11]考虑了光伏出力和旋转负荷的不确定性,采用概率模型对其进行估算,在此基础上建立了以运行成本最小的ADN经济优化调度模型,利用CPLEX求解器对模型进行了求解,得到了ADN最小运行成本。上述模型均未考虑售电收益,其经济性有待进一步提高。文献[12]考虑到目标函数内状态变量的越界情况,利用多区域全分布算法建立了基于多区域全分布算法的ADN动态经济调度模型,利用改进粒子群算法进行求解,实现了ADN的动态性经济调度,该模型忽略了储能设备损耗成本。综上所述,现有ADN优化调度模型存在优化目标不明确、约束条件不够完善等问题,经济性更好的ADN优化调度模型有待进一步研究。
针对上述问题,本文综合考虑ADN运行过程中的各项成本,以调度周期内ADN运行成本最小为目标函数,考虑各类约束条件,建立基于改进樽海鞘群算法(Improved Salp Swarm Algorithm,ISSA)的ADN经济优化调度模型,采用改进的IEEE33节点配电系统对模型的正确性和求解方法的优越性进行验证。
1 ADN经济优化调度模型 1.1 目标函数为了提高配电网运行的经济性和提高再生能源的消纳能力,将综合考虑分时电价和分布式储能对ADN运行的影响,本文将功率交互成本、损耗成本和分布式储能设备投资成本之和作为优化目标,以调度周期内ADN运行成本最小为目标函数,建立ADN经济优化调度模型,具体如下:
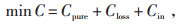
|
(1) |
式中:C为ADN运行成本;Cpure为功率交互成本;
Closs为损耗成本;Cin为分布式储能设备投资成本。
1.1.1 功率交互成本功率交互成本Cpure主要包括向上级电网购电产生的购电成本、向上级电网售电产生的售电收益和向系统内DG购电产生的购电成本,其表达式为:
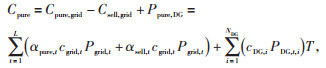
|
(2) |
式中:Cpure, grid为向上级电网购电产生的购电成本,Csell, grid为向上级电网售电产生的售电收益,Cpure, grid和Csell, grid在同一时段必有一个为0;Ppure, DG为向系统内DG购电产生的购电成本;L为调度周期内的总时段,本文取24;T为各时段时长,本文取1 h;αpure, t、αsell, t均为购、售电参量,购电时满足αpure, t = 1,αsell, t = 0,售电时αpure, t = 0,αsell, t = 1。cgrid, t为向上级电网购、售电电价;Pgrid, t为交互功率,购电为正,售电为负;NDG为DG总量;PDG, t, i为第i台DG的输出功率;cDG, i第i台为DG的购电电价。
1.1.2 损耗成本损耗成本Closs主要包括系统网络损耗成本和储能设备损耗成本,其表达式为:
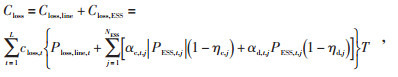
|
(3) |
式中:Closs, line为系统网络损耗成本;Closs, ESS为储能设备损耗成本;closs, t为损耗电价,其值与cgrid, t相同;Ploss, line, t为t时段的网损;NESS为储能设备总量;αc, t, j、αd, t, j均为储能设备充放电参量;PESS, t, j为第j台储能设备在t时段的充、放电功率,充电时满足αc, t, j = 1、αd, t, j = 0、PESS, t, j < 0,放电时满足αc, t, j = 0、αd, t, j = 1、PESS, t, j > 0;ηc, j和ηd, j分别为第j台储能设备的充、放电效率。
1.1.3 分布式储能设备投资成本分布式储能设备投资成本Cin的表达式为:
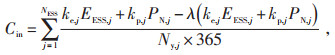
|
(4) |
式中,ke, j为第j台储能设备单位容量管理成本;EESS, j为第j台储能设备的容量;kp, j为第j台储能设备单位功率转换成本;PN, j为第j台储能设备的额定功率;Ny, j为第j台储能设备的使用年限;λ为折旧率。
1.2 约束条件 1.2.1 网络运行约束
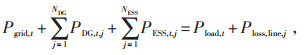
|
(5) |
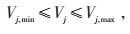
|
(6) |
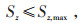
|
(7) |
式中:Pload, t为ADN系统在t时段的负荷;Vj为节点j的电压标幺值;Vj, max为节点i电压上限,本文取1.05;Vj, min为节点j电压下限,本文取0.95;Sz为第z条支路的视在功率;Sz, max为Sz的上限。
1.2.2 DG运行约束
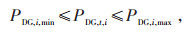
|
(8) |
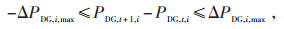
|
(9) |
式中:PDG, i, min和PDG, i, max分别为第i个DG输出功率的上限和下限;ΔPDG, i, max为第i个DG在相邻两个时段允许调整的最大输出功率。
1.2.3 分布式储能约束
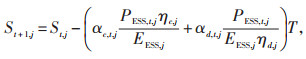
|
(10) |
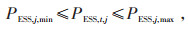
|
(11) |
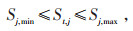
|
(12) |
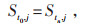
|
(13) |
式中:PESS, j, max和PESS, j, min分别为第j台储能设备充、放电功率上限和下限;St, j为第j台储能设备在t时段的荷电状态;Sj, max和Sj, min分别为St, j的上限和下限;St0, j和Stn, j分别为第j台储能设备在调度开始时段和结束时段的荷电状态。
2 ISSA原理 2.1 樽海鞘群算法2017年,Mirjalili等人提出了一种新型启发式优化算法——樽海鞘群算法(Salp Swarm Algorithm,SSA)[13],它是根据樽海鞘种群的觅食行为提出来的。SSA算法的原理如下:将种群划分为领导者和追随者,领导者的作用是带领追随者寻找食物,令食物为G,樽海鞘群在d维空间中的位置矩阵设为Sn×d,其中元素si, j表示第i个樽海鞘在第j维搜索空间的位置,n表示樽海鞘种群容量。
SSA算法中的领导者依据食物位置更新自身位置,领导者的位置更新公式为:
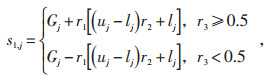
|
(14) |
式中:Gj为领导者的位置;uj为第j维空间的上限值;lj为第j维空间的下限值;r1、r2、r3均为调整系数,r1、r2∈[0, 1],r1的计算公式如下:
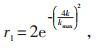
|
(15) |
式中:k为当前迭代次数;kmax为最大迭代次数。追随者跟随领导者的位置移动,追随者的位置更新公式为:
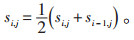
|
(16) |
SSA算法的优点是原理简单、操作方便,其缺点是易陷入局部极值[14]。
2.2 ISSA针对SSA算法的不足,采用下列三种策略对其进行改进,具体如下。
2.2.1 莱维飞行莱维飞行可以提高种群多样性,本文在樽海鞘群领导者位置更新时引入莱维飞行策略,以便增强算法的全局搜索性能。具体改进如下:
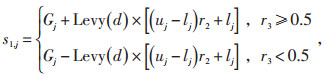
|
(17) |
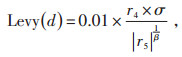
|
(18) |
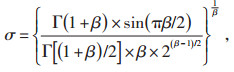
|
(19) |
式中:r4、r5均为随机数,取值范围为[0, 1];Levy表示莱维飞行;Γ表示Gamma函数,其概率分布的均值和方差都是无界的。
2.2.2 非线性收敛因子在SSA算法中,追随者的位置取决于当前个体和上一个体的位置,这样位置更新策略不利用算法收敛,为此,将收敛因子非线性调整策略引入该过程,以加快算法收敛。具体如下:
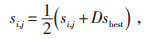
|
(20) |
式中:sbest为当前最优个体位置;D为收敛因子,其作用是对最优值的比重进行调整,使算法快速收敛,其计算公式为:
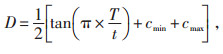
|
(21) |
式中:cmin、cmax为学习因子。
2.2.3 柯西变异针对SSA算法在迭代后期已陷入局部最优的不足,本文对当前最优解执行柯西变异,以增强算法的局部寻优能力。柯西概率密度函数的表达式为:
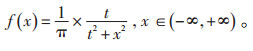
|
(22) |
将当前最优解执行式(23)中的柯西变异,其表达式为:
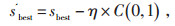
|
(23) |
式中:s'best为变异后的最优个体位置;C(0, 1) 是指服从柯西变异的樽海鞘个体;η为常数。
2.3 算法性能测试采用Sphere和Ackely两个常用的测试函数对ISSA算法优化性能进行验证,两个函数分别用f1和f2表示,其数学表达式分别如式(24)和式(25)所示,f1的搜索范围为[-100, 100],f2的搜索范围为[-20, 20],两个函数的维度均为30维,全局最优解均为0。
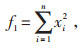
|
(24) |
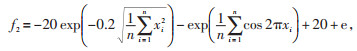
|
(25) |
式中:xi为函数自变量。
ISSA算法参数设置如下[17]:樽海鞘种群n=30、最大迭代次数kmax=500,学习因子cmin=0.004、cmax=1。
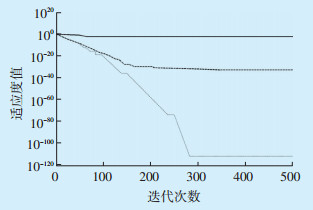
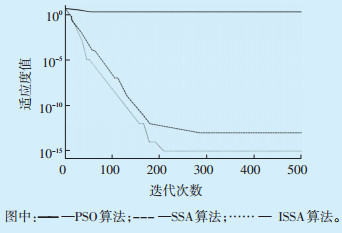
为了对比分析,采用粒子群优化算法(Particle Swarm Optimization,PSO)与SSA算法对两个测试函数进行优化,三种算法对函数和的优化结果分别如图 1和图 2所示。图 1中,PSO算法、SSA算法和ISSA算法找到的最优解分别为4.46×10-3、2.78×10-32和1.27×10-112;图 2中,PSO算法、SSA算法和ISSA算法找到的最优解分别为1.744、3.69 × 10-13和2.86 × 10-15。由此可见,ISSA算法的收敛精度提升明显,寻优能力大大提升。
|
| 图 1 f1优化结果 Figure 1 Optimization results of f1 图中:———PSO算法;---—SSA算法;…… — ISSA算法。 |
|
| 图 2 f2优化结果 Figure 2 Optimization results of f2 图中:———PSO算法;---—SSA算法;…… — ISSA算法。 |
为了满足ADN系统功率平衡约束并实现ADN与上级电网的等效隔离,将它们之间的连接点作为平衡节点。对于不等式约束,当调度方案无法满足时,利用罚函数进行处理,罚函数的表达式为:
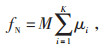
|
(26) |
式中:K为调度方案中不满足不等式约束的个数和;M为罚因子,本文取值为105;μi为惩罚系数,如果约束不满足,则惩罚成立,此时μi = 1;在模型求解过程中,将罚函数fN加到目标函数中,可以剔除所有不满足约束条件的调度方案。
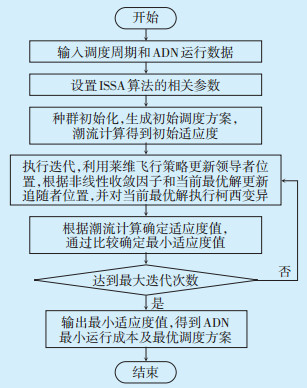
3.2 求解步骤采用ISSA算法对ADN经济优化调度模型进行求解,流程如图 3所示。
|
| 图 3 ISS算法求解流程图 Figure 3 Solution flowchart of ISS algorithm |
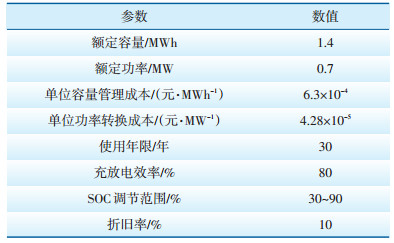
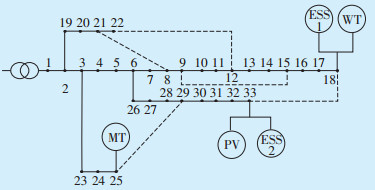
采用改进的IEEE33节点配电系统进行仿真分析,系统参数可参考文献[15],其网络拓扑结构如图 4所示,其中,节点1为平衡节点,其电压与上级电网母线电压相同,为12.66 V。节点2—33为局面负荷节点,节点18接入一个装机容量为1 MW的风电场和一组储能电池,节点33接入一个装机容量为1 MW的光伏电站和另一组储能电池,节点25接入额定功率为0.8 MW的微型燃气轮机。两组蓄电池参数完全相同,具体如表 1所示。
|
| 图 4 改进的IEEE33网络拓扑结构 Figure 4 Improved IEEE33 network topology |
| 表 1 储能电池参数 Table 1 Energy storage battery parameters |
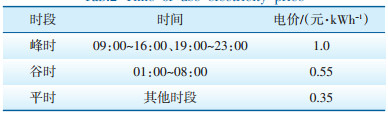
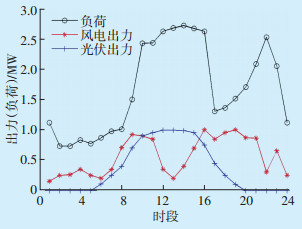
设置调度周期为24 h,将一天分为24个时段,图 5给出了调度日当天风电、光伏出力及负荷变化情况。根据国家电网公司颁布的DG接入电网电价标准[16],设置配电网向光伏、风电和微型燃气轮机的购电电价分别为1元、1元和0.81元。ADN与上级电网功率交互电价和系统损耗电价均采用分时电价,具体如表 2所示。
|
| 图 5 光伏、风电、负荷预测值 Figure 5 Predicted values of photovoltaic, wind power and load |
| 表 2 分时电价 Table 2 Time of use electricity price |
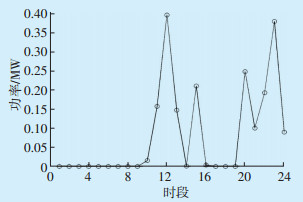
通过Matlab软件进行仿真分析,调度日当天微型燃气轮机各时段输出功率如图 6所示。由图 6可知,在低谷电价时段(时段1—8)和平电价时段(时段1、时段9、时段17—19),购电电价较低,优先向上级电网购电,微型燃气轮机处于停机状态;在高峰电价时段(时段10—16、时段20—23),购电电价较高,采用微型燃气轮机发电比购电更划算,微型燃气轮机输出功率以满足系统负荷需求,从而降低功率交互成本和网络损耗成本。
|
| 图 6 微型燃气轮机各时段输出功率 Figure 6 Output power of micro gas turbine at different time periods |
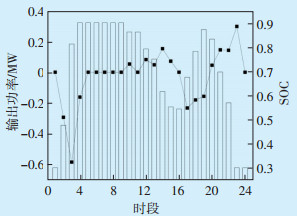
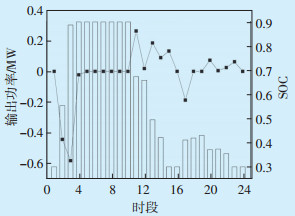
储能电池1和储能电池2的输出功率及SOC变化情况分别如图 7和图 8所示。由图 7和图 8可知,在低谷电价时段(时段1—8),储能电池1和2均处于充电状态;在高峰电价时段(时段10—16、时段20—23),储能电池1和2均处于放电状态,以减少向上级电网购电;在平时段(时段15—19),储能电池1和2也处于充电状态,其原因在于该时段的前后均为高峰电价时段,此时段充电可以降低时段20—23的购电成本,由此可见,储能电池实现了低储高发运行策略,节约了购电成本。
|
图 7 储能电池1输出功率及SOC变化情况
Figure 7 Output power and SOC changes of energy storage battery 1
图中: —输出功率; —输出功率; —SOC。 —SOC。
|
|
图 8 储能电池2输出功率及SOC变化情况
Figure 8 Output power and SOC changes of energy storage battery 2
图中: —输出功率; —输出功率; —SOC。 —SOC。
|
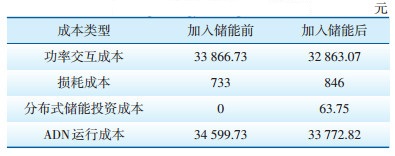
表 3给出了ADN加入储能电池前后各项成本对比情况,对比表 3中的数据可知,储能电池投入后系统网络损耗成本虽然下降了,但储能电池本身也存在损耗成本,导致网络损耗成本有所增加。但加入储能电池后,功率交互成本明显下降,使AND运行成本降低826.91元,提高了经济效益。
| 表 3 加入储能电池前后各项成本对比 Table 3 Comparison of various costs before and after adding energy storage batteries |
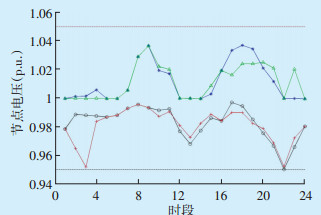
在调度周期内加入储能电池前后各时段节点电压分布情况见图 9。由图 9可知,加入储能电池前,节点电压最大值和最小值分别为1.037 7(p.u.)和0.950 2(p.u.),存在电压越下限的风险;加入储能电池后,节点电压最大值和最小值分别为1.037 5(p.u.)和0.952 1(p.u.),解除了电压越下限的风险,节点电压波动范围进一步减小,电压质量得到改善。
|
图 9 节点电压分布情况
Figure 9 Distribution of node voltage
图中: —未加储能电池前最低电压; —未加储能电池前最低电压; —未加储能电池前最高电压; —未加储能电池前最高电压; —加入储能电池前最低电压; —加入储能电池前最低电压; —加入储能电池前最高电压; —加入储能电池前最高电压; —节点电压下限; —节点电压下限; —电压幅值上限。 —电压幅值上限。
|
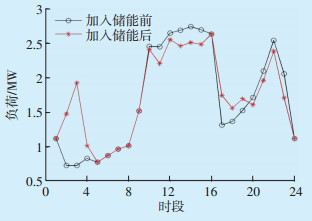
为了进一步对比分析,将系统负荷与储能电池充放电功率作为一个整体,形成等效负荷曲线,加入储能前后的等效负荷曲线如图 10所示。由图 10可知,加入储能电池后,等效负荷曲线峰谷差有所减小,说明储能电池实施低储高发策略可以实现削峰填谷,改善负荷曲线[17-18]。
|
| 图 10 加入储能电池前后的等效负荷曲线 Figure 10 Equivalent load curve before and after adding energy storage batteries |
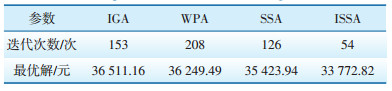
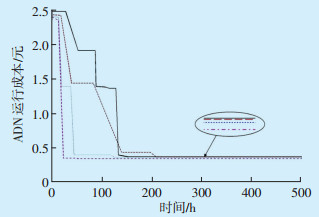
为了验证ISSA算法在求解ADN经济优化调度模型中的优越性,采用改进遗传算法(Improved Genetic Algorithm,IGA)与狼群优化算法(Wolf Pack Algorithm,WPA)及SSA算法对本文模型进行求解,图 11给出了四种算法的迭代收敛曲线。由图 11可知,相比其他3种优化算法,ISSA算法收敛时所需的迭代次数更少,所求得的ADN运行成本最小,可见ISSA算法的优化效果更好。表 4给出了四种算法的优化结果及收敛至最优解时的迭代次数。由表 4可知,在迭代次数方面,ISSA算法相比IGA、WPA和SSA算法分别减少99次、154次和72次;在最优解方面,ISSA相比IGA、WPA和SSA算法分别降低2738.34元、2476.67元和1651.12元,可见ISSA算法的迭代次数更少,计算精度更高,验证了本文所提ADN经济优化调度方法的实用性。
|
图 11 四种算法收敛曲线对比
Figure 11 Comparison of convergence curves of four algorithms
图中: —IGA算法; —IGA算法; —WPA算法; —WPA算法; —SSA算法; —SSA算法; —ISSA算法。 —ISSA算法。
|
| 表 4 四种算法优化结果 Table 4 Optimized results of four algorithms |
综合考虑分时电价和分布式储能对ADN的影响,本文提出了一种考虑分时电价和分布式储能的ADN优化调度方法,采用莱维飞行、非线性收敛因子和柯西变异等策略对SSA算法进行改进,使ISSA算法跳出局部最优的能力显著增强,收敛精度明显提升,利用ISSA算法对ADN优化调度模型进行了求解。算例分析结果表明,在制订ADN优化调度策略时考虑分时电价和分布式储能的作用,能够实现削峰填谷、改善负荷曲线和降低微电网运行成本,提高ADN运行的稳定性和经济性,该方法为ADN调度提供了一种新思路。
| [1] |
袁海山, 叶昀, 陈有强, 等. 基于能源互联网技术的电网分布式电源布置研究[J].
电网与清洁能源, 2023, 39(3): 136-142 YUAN Haishan, YE Yun, CHEN Youqiang, et al. Research on distributed power generation layout in power grid based on energy internet technology[J]. Power System and Clean Energy, 2023, 39(3): 136-142 (  0) 0)
|
| [2] |
李雪, 李博, 姜涛, 等. 主动配电网潮流的全纯嵌入计算方法[J/OL]. 中国电机工程学报: 1-14[2023-05-06]. http://kns.cnki.net/kcms/detail/11.2107.TM.20230307.1809.007.html.
LI Xue, LI Bo, JIANG Tao, et al. A holomorphic embedding calculation method for active distribution network power flow[J/OL]. Chinese Journal of Electrical Engineering: 1-14[2023-05-06]. http://kns.cnki.net/kcms/detail/11.2107.TM.20230307.1809.007.html. (  0) 0)
|
| [3] |
马燕峰, 谢家荣, 赵书强, 等. 考虑园区综合能源系统接入的主动配电网多目标优化调度[J].
电力系统自动化, 2022, 46(13): 53-61 MA Yanfeng, XIE Jiarong, ZHAO Shuqiang, et al. Multi objective optimization scheduling of active distribution networks considering the integration of park integrated energy systems[J]. Automation of Electric Power Systems, 2022, 46(13): 53-61 (  0) 0)
|
| [4] |
虎智峰, 陈静, 张婧菲, 等. 考虑新能源不确定性边界的主动配电网优化调度[J].
智慧电力, 2022, 50(11): 48-55 HU Zhifeng, CHEN Jing, ZHANG Jingfei, et al. Optimal scheduling of active distribution networks considering the uncertainty boundary of new energy[J]. Smart Power, 2022, 50(11): 48-55 (  0) 0)
|
| [5] |
乐健, 綦淦, 赵联港, 等. 主动配电网分布式经济调度系统的时延稳定性分析[J].
电力系统保护与控制, 2022, 50(21): 75-87 LE Jian, QI Gan, ZHAO Liangang, et al. Delay sStability analysis of active distribution network distributed economic dispatching system[J]. Power System Protection and Control, 2022, 50(21): 75-87 (  0) 0)
|
| [6] |
杨晓辉, 张柳芳, 吴龙杰, 等. 含考虑IDR的冷热电联供微网的主动配电网经济优化调度[J].
电力系统保护与控制, 2022, 50(3): 19-28 YANG Xiaohui, ZHANG Liufang, WU Longjie, et al. Economic optimization and dispatching of active distribution networks including IDR considered combined cooling, heating, and power supply microgrids[J]. Power System Protection and Control, 2022, 50(3): 19-28 (  0) 0)
|
| [7] |
吴成国, 肖仕武. 高比例分布式电源接入电网短路电流的拟牛顿迭代计算方法[J].
电网技术, 2022, 46(12): 4581-4591 WU Chengguo, XIAO Shiwu. Quasi Newton iterative calculation method for short-circuit current of high proportion distributed power sources connected to the power grid[J]. Power System Technology, 2022, 46(12): 4581-4591 (  0) 0)
|
| [8] |
招景明, 苏洁莹, 潘峰, 等. 考虑光伏波动的有源配电网分布式储能双目标优化规划[J].
可再生能源, 2022, 40(11): 1546-1553 ZHAO Jingming, SU Jieying, PAN Feng, et al. Dual objective optimization planning for distributed energy storage in active distribution networks considering photovoltaic fluctuations[J]. Renewable Energy Resources, 2022, 40(11): 1546-1553 (  0) 0)
|
| [9] |
齐鹏辉, 韦洪波, 江雄烽, 等. 基于数据自适应鲁棒优化的主动配电网经济调度方法[J/OL]. 电测与仪表: 1-8[2023-05-06]. http://kns.cnki.net/kcms/detail/23.1202.TH.20220602.1850.011.html.
QI Penghui, WEI Hongbo, JIANG Xiongfeng, et al. An active distribution network economic dispatching method based on data adaptive robust optimization[J/OL]. Electrical Measurement and Instrumentation: 1-8[2023-05-06]. http://kns.cnki.net/kcms/detail/23.1202.TH.20220602.1850.011.html. (  0) 0)
|
| [10] |
李军徽, 马得轩, 朱星旭, 等. 基于ADMM算法的主动配电网分层优化经济调度[J].
电力建设, 2022, 43(8): 76-86 LI Junhui, MA Dexuan, ZHU Xingxu, et al. Active Distribution Network Layered Optimization Economic Dispatch Based on ADMM Algorithm[J]. Electric Power Construction, 2022, 43(8): 76-86 (  0) 0)
|
| [11] |
孟令卓超, 杨锡运, 赵泽宇. 考虑光-荷不确定性和旋转备用约束的主动配电网经济优化调度策略[J].
电力建设, 2022, 43(11): 63-72 MENG Lingzhuochao, YANG Xiyun, ZHAO Zeyu. An economic optimal dispatching strategy for active distribution networks considering light load uncertainty and rotating reserve constraints[J]. Electric Power Construction, 2022, 43(11): 63-72 (  0) 0)
|
| [12] |
杨占杰, 谢虎, 张伟, 等. 基于多区域全分布算法的主动配电网动态经济调度方法[J/OL]. 电测与仪表: 1-10[2023-05-06]. http://kns.cnki.net/kcms/detail/23.1202.TH.20220402.1918.007.html.
YANG Zhanjie, XIE Hu, ZHANG Wei, et al. A Dynamic economic dispatching method for active distribution networks based on multi region fully distributed algorithm[J/OL]. Electrical Measurement and Instrumentation: 1-10[2023-05-06]. http://kns.cnki.net/kcms/detail/23.1202.TH.20220402.1918.007.html. (  0) 0)
|
| [13] |
沈平, 张彬彬, 袁瑛. 樽海鞘群算法在可见光通信调制器的应用[J].
光学技术, 2021, 47(4): 477-482 SHEN Ping, ZHANG Binbin, YUAN Ying. Application of the Zunhei sheath swarm algorithm in visible light communication modulators[J]. Optical Technique, 2021, 47(4): 477-482 (  0) 0)
|
| [14] |
黄小根, 钟尚勤. 一种多策略驱动的改进樽海鞘群算法[J].
计算机仿真, 2022, 39(1)308-311, 357 HUANG Xiaogen, ZHONG Shangqin. A multi strategy driven improved cunninghamia scabbard swarm algorithm[J]. Computer Simulation, 2022, 39(1)308-311, 357 (  0) 0)
|
| [15] |
张煜, 牟龙华, 王蕴敏, 等. 计及可控负荷动态调节的主动配电网优化调度[J].
电力系统保护与控制, 2021, 49(4): 104-110 ZHANG Yu, MOU Longhua, WANG Yunmin, et al. Active distribution network optimization scheduling considering controllable load dynamic regulation[J]. Power System Protection and Control, 2021, 49(4): 104-110 (  0) 0)
|
| [16] |
李艳梅, 任恒君, 张致远, 等. 考虑储能系统调度与风电消纳的峰谷分时电价优化模型研究[J].
电网技术, 2022, 46(11): 4141-4149 LI Yanmei, REN Hengjun, ZHANG Zhiyuan, et al. Study on the optimization model of peak valley time of use electricity price considering energy storage system scheduling and wind power consumption[J]. Power System Technology, 2022, 46(11): 4141-4149 (  0) 0)
|
| [17] |
韩子娇, 李宠, 苑舜, 等. 风电制氢混合储能系统容量优化配研究[J].
东北电力技术, 2022, 43(10): 56-62 HAN Zijiao, LI Chong, YUAN Shun, et al. Research on optimal allocation of hybrid energy storage system capacity for wind power hydrogen production[J]. Northeast Electric Power Technology, 2022, 43(10): 56-62 (  0) 0)
|
| [18] |
方胜利, 朱晓亮, 马春艳, 等. 基于电力物联网的光储微网协同控制系统设计[J].
机电工程技术, 2023, 52(6): 186-191 FANG Shengli, ZHU Xiaoliang, MA Chunyan, et al. Design of optical storage microgrid cooperative control system based on power internet of things[J]. Mechanical & Electrical Engineering Technology, 2023, 52(6): 186-191 (  0) 0)
|
 2023, Vol. 41
2023, Vol. 41