目前,蓄电池构成的储能系统广泛应用于微电网和新能源汽车等领域。为满足储能系统的电压和功率要求,需要将单体蓄电池通过串并联的形式组成蓄电池组。串并联蓄电池组各个单体电池由于生产和工作环境等原因,会产生不一致性[1]。单体蓄电池将直接影响整个电池组的寿命、容量等性能,为避免出现“短板效应”,需要及时对蓄电池进行均衡控制,从而消除差异,保证蓄电池组能量的高效利用。
如何准确地建立电池模型以实现电池数据监测、荷电状态(State of Charge,SOC)估算等一直是研究重点。Rint是等效电路模型中最为简单的内阻模型,但容易受电池状态及环境变化的影响,文献[2]对Rint模型改进,将电池内阻分为欧姆电阻和极化内阻。Thevenin在Rint的基础上添加了一个RC环节,文献[3]研究表明一阶RC等效电路欧姆内阻参数的变化具有复杂的动力学行为。PNGV模型在Thevenin模型的基础上增加了一个电容[4-5],但是精度提升有限,运算更为复杂。GNL模型在PNGV模型的基础上串联了两个RC环节,结构更加复杂,精度更高,能够较好地体现蓄电池的化学特性和电特性[6-7]。Massimo Ceraolo模型虽然精度很高,但是过于复杂,参数辨识难度很大[8]。
随着锂电池种类和模型的快速发展,SOC的估计方法也增多。安时积分法不适合长时间估计SOC,长期单独使用将会引入较大的误差,仅适用于短时内准确估计SOC[9]。文献[10-11]通过精简的开路电压法快速并相对准确地估算了磷酸铁锂电池的SOC。为了解决安时积分法不能确定电池SOC初始值和开路电压法需要电池长时间静置的问题,文献[12]提出使用安时积分法与开路电压法相结合的方法估计电池SOC值。放电实验法是通过放电的形式进行SOC估计,但需要将电池停止工作,并且放电时间较长,不适用于在线估计SOC。卡尔曼滤波算法主要通过噪声方差和递归的协方差矩阵修正目标状态,对SOC的估计精度较高,对初始值依赖小,自适应能力强[13-16]。文献[17-19]应用神经网络算法对电池SOC进行事实估计,但在实际使用前,需要建立合适的网络模型并输入大量的样本数据进行训练与学习,准备工作较为复杂。
目前,实现电池组的均衡控制,主要的方法是在拓扑中加装均衡电路[20]。均衡电路拓扑按照能量耗散方式可分为主动均衡和被动均衡,被动均衡主要是通过外接电阻实现分流放电进行均衡,速度慢,均衡效率低,虽然文献[21]重新设计与改造了被动均衡电路,能量损耗和均衡时间都有所减少,但是主动均衡控制已成为近几年的主要研究对象。主动均衡主要利用储能元件,采用集中控制等方法实现电池能量的转移[22-23]。电容均衡具有反应速度快、功率密度高和循环寿命长等优点,适用于电池均衡电路[24],但基于储能电容的均衡电路只能以端电压为均衡准则,不能实现SOC均衡,当两节电池电压相差较小时,均衡速度较慢。文献[25]提出了一种基于串并联开关电容的均衡电路,将最大电压电池中的能量高效快速地转移到其他小电压电池中,缩短了能量传输路径,提高了均衡速度。电感型均衡电路均衡速度快,均衡效率高,但是开关控制复杂[26]。文献[27]提出了一种混合开关电容和开关电感的新型均衡电路,其与传统开关电容均衡电路相比具有更快的均衡速度。文献[28]对经典Buck-Boost电路进行改进后作为串联电池组均衡单元,开关器件有所减少,可实现低功耗高效率。传统的Buck-Boost变换器均衡电路控制简单,均衡速度快,能量损耗小,但是当两节电池距离较远时,能量逐级传递,不仅增加了均衡时间,也降低了均衡效率[29]。Cuk变换器均衡电路可以实现相邻两节电池间的能量转移,均衡电流连续,具有更高的均衡速度[30]。
本文主要针对串联蓄电池组的差异性问题进行均衡研究,选用二阶RC等效电路作为电池模型,对比常用的几种均衡拓扑,选择基于Cuk的均衡电路作为主电路,并制定相应的均衡电流控制策略,最大电流设计为40 A。采用SOC作为均衡依据,通过混合脉冲功率特性(Hybrid Pulse Power Charaterzation,HPPC)实验进行参数辨识,使用扩展卡尔曼滤波(Extended Kalman Filter,EKF)对SOC进行估计。选用额定容量为60 Ah,额定电压为3.3 V的磷酸铁锂动力蓄电池进行实验,在硬件平台实现均衡电流控制。
1 均衡方案整体设计 1.1 均衡依据判断蓄电池不平衡的标准主要有单体电池的端电压和单体电池的SOC。在进行均衡控制时,电池端电压与SOC具有一一对应的关系,通过比较各蓄电池的端电压进行均衡控制[31],但当电池在动态过程中或大电流下,电池端电压与SOC呈非线性关系,当SOC在40%~80%时,端电压变化不明显,当SOC在0~40%以及80%~100%时,端电压变化相对明显。当电池处于充放电状态下时,因为电池的内部结构和极化效应的影响,电池端电压还会出现上升和下降的现象。
随着蓄电池的使用,其内阻会逐渐增大,容量将减小,这就导致开路端电压与SOC的对应关系逐渐改变。而SOC估计能够增加电池寿命和温度等影响SOC的因素系数,从而避免电池的SOC估计不准确。同时,针对不同的工作电流,电池的端电压也不一样,并不能表示出电池的剩余电量,而SOC可以直接表示。因此本文以单体蓄电池的SOC作为均衡依据,对串联蓄电池组进行控制。
1.2 均衡拓扑选择根据本文所控制的均衡电流,均衡拓扑选择基于Cuk变换器的均衡电路。该均衡电路类似于Buck-Boost的双向均衡电路,可实现能量的双向流动,但相较于Buck-Boost的双向均衡电路的蓄电池电流,基于Cuk的双向均衡电路的蓄电池电流可以连续流动。
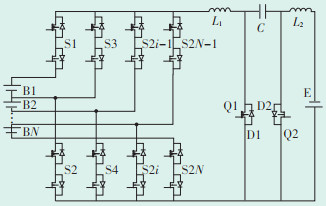
基于Cuk的双向双层桥臂均衡电路如图 1所示。该均衡电路主要分为两部分,左半部分为双层桥臂结构,用来选择需要进行均衡控制的单体蓄电池;右半部分为基于Cuk的均衡主电路,执行均衡功能,控制能量的双向流动。B1—BN为蓄电池组,双向桥臂开关矩阵电路由上、下桥臂功率开关矩阵S构成,均由n对反向串联的功率MOSFET开关组成的双层功率开关矩阵。均衡主电路是双向Cuk电路,由储能元件电感L1、L2,电容C,电压源E,两个主控开关Q1和Q2构成,D1和D2为二极管,通过主控开关的脉宽调制控制(Pulse Width Modulation,PWM)使均衡能量在单体电池与均衡电路之间转移。电池组充电时通过降低电池组中电压或SOC最高单体电池的充电电流来提高整个电池组的充电容量;电池组放电时通过降低电池组中电压或SOC最低单体电池的放电电流来提高整个电池组的放电容量。这种双层桥臂的均衡电路一方面可以防止均衡过程中电池短路,另一方面可以实现能量通过Cuk电路双向流动,从而实现充电均衡和放电均衡。
|
| 图 1 基于Cuk的双向双层桥臂均衡电路 Figure 1 Bidirectional double-deck bridge arm equalization circuit based on Cuk |
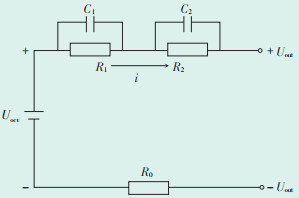
选用电气模型中的二阶RC等效电路模型,如图 2所示。二阶RC等效电路模型在一阶Thevenin等效电路模型的基础上,多增加了一个一阶RC电路。其中,一个RC电路用来表示电化学极化效应,另一个RC电路表示浓差极化效应。该模型能够良好的反应电池的内阻和瞬间响应,表现电池在工作状态下的稳态特性和暂态特性,结构简单,模型精度较高。
|
| 图 2 二阶RC等效电路模型 Figure 2 Second-order RC equivalent circuit model 图中:Uout为电池两端电压;Uocv为电池内部电压,该参数在一定情况下与该电池的SOC有固定的映射关系;C1、C2为电容;R1、R2为极化电阻;i为放电电流;R0为电池内阻,在冲放电过程中会引起电池输出电压Uout的突变。 |
模型的数学表达式如式(1)所示:
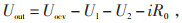
|
(1) |
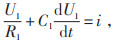
|
(2) |
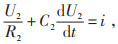
|
(3) |
式中:U1、U2分别为电容C1、C2两端电压,V;t为时间,s。
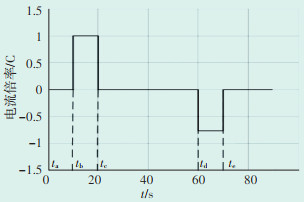
2.2 参数辨识确定电池的等效电路模型后,根据所选模型对其各个电路元件进行参数辨识,以便使用扩展卡尔曼滤波(EKF)对电池进行SOC估计。据FreedomCar手册中介绍的HPPC实验[32],主要分为三段,如图 3所示。电池进行10 s的1 C电流放电,40 s的静置时间,10 s的0.75 C电流充电。每完成1次HPPC实验阶段,则对电池放电10%的SOC进行估计,然后静置1 h,准备下一次HPPC实验。
|
| 图 3 HPPC实验 Figure 3 HPPC experimentt 图中:ta—tb为电池静置时间;tb—tc为恒定1 C电流放电10 s;tc—td为电池静置40 s;td—te为恒定0.75 C电流充电10 s。 |
以1 s作为采样时间间隔,记录电池在实验中的电流和端电压等数据。根据文献[33]中介绍的HP-PC实验参数辨识方法,在HPPC的静置时段,属于零输入响应,结合上文选取的二阶RC等效电路模型列写零输入响应的表达式:
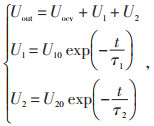
|
(4) |
式中:τ1、τ2分别为两组RC的时间常数,s;U10、U20分别为两组极化电压的初始值,V。
在HPPC实验的放电时段,属于零状态响应,结合上文选取的二阶RC等效电路模型列写零状态响应的表达式:
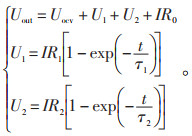
|
(5) |
根据式(4)和式(5),使用Matlab工具箱进行曲线拟合,可以分别得到时间常数τ1、τ2和极化电阻R1、R2。
根据上文中提到的放电电阻,在10%的SOC放电结束时刻和1 h静置开始时刻,根据压降和放电电流计算得到放电电阻值。因为HPPC不能在每一个SOC点进行实验,所以放电每隔10%的SOC就进行一次HPPC实验,从而得到一组等效电路的参数。但蓄电池在实际使用中,SOC和电池参数都随蓄电池的工作时间连续变化,所以需要根据辨识的参数进行曲线拟合,得到每一个SOC点所对应的电池参数,以便于进行后面的SOC估计。
2.3 SOC估计利用改进的卡尔曼滤波直接对非线性系统状态进行估计的方法叫做扩展卡尔曼滤波(EKF),适用于非线性系统。本文基于EKF进行SOC估计,该方法利用安时积分法短时间估计SOC的准确性,通过开路电压法弥补安时积分法长时间估计SOC存在较大误差和SOC初始值估计不准确的缺点,再结合卡尔曼滤波法滤除过程噪声和测量噪声,从而对SOC进行估计并矫正,得到当前SOC的最优估计值。
非线性离散系统的状态方程和观测方程如式(6)和(7)所示:
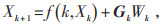
|
(6) |
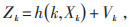
|
(7) |
式中:k为时刻;Xk和Xk+1分别为系统k时刻和k+1时刻的状态;Gk为k时刻噪声驱动矩阵;Wk为k时刻过程噪声,均值为零的高斯白噪声;Vk为k时刻测量噪声,Zk为k时刻测量值。
首先,扩展卡尔曼滤波将非线性函数进行局部线性化处理。由式(6)的系统状态方程将非线性函数f(*)围绕状态量估计值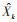
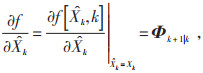
|
(8) |
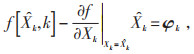
|
(9) |
得到状态方程为:
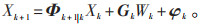
|
(10) |
由式(7)的观测方程,将非线性函数h(*) 围绕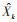
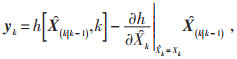
|
(11) |
得到观测方程为:
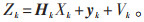
|
(12) |
然后,对线性化后的模型(8)和(9)应用线性卡尔曼滤波便可得到递推方程式(13)—(17):
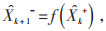
|
(13) |
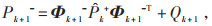
|
(14) |
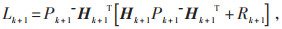
|
(15) |
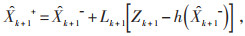
|
(16) |
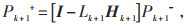
|
(17) |
式中: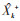
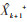
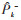
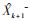
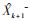
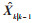
结合选取的二阶RC等效电路和文献[34]介绍的基于EKF估计SOC的方法,建立二阶RC等效电路模型的状态方程。状态变量分别选取荷电状态SOC、第一组RC电压U1和第二组RC极化电压U2,控制量为电流I。二阶RC等效电路的状态方程为公式(18),其中SOC式中记为S:
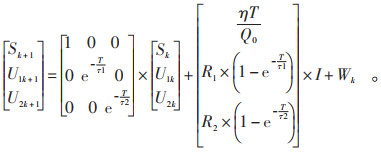
|
(18) |
观测方程为:
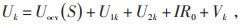
|
(19) |
式中:T为采样时间,s;Q0为电池以1C倍率放电所能释放的电量,C;η为库仑系数,可以通过电池充放电实验得到;U1k和U1k+1、U2k和U2k+1分别为k和k+1时刻的电容C1、C2两端的电压,V。
通常,式(14)中Qk+1设为0,式(15)中观测噪声Rk+1的协方差矩阵符合高斯分布,由电池充放电截止电压决定。由式(6)—(19)可得到SOC估算结果。
2.4 控制策略为满足低损耗和高速率均衡,本文使用恒定电流,均衡过程中产生的损耗为:
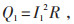
|
(20) |
式中:Q1—损耗能量,C;
I1—恒定的均衡电流,A;
R—均衡过程中的损耗电阻,Ω;
t—均衡时间,s。
如果使用矩形波电流进行均衡,占空比为50%,那么使用矩形波电流需要花费恒定电流2倍的时间才能完成均衡。如果让两种类型的均衡电流在相同的时间内完成均衡,那么矩形波电流的幅值就需要增大,使电流对时间的积分面积等于对应相同时间的恒定电流对时间的积分面积。所以矩形波电流I1与恒定电流I2的关系为:
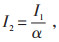
|
(21) |
式中:α—矩形波的占空比,%。
因此矩形波电流在一个开关周期内进行均衡的损耗为:
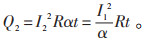
|
(22) |
占空比α的变化范围为0~100%,可以得到结论为:Q2>Q1。
在相同均衡速度前提下,矩形波电流均衡损耗大于恒定电流均衡损耗,所以本文选用基于Cuk电路的均衡电路。利用Cuk电路中电感电流连续和纹波小的特点,进行恒定电流均衡,制定了基于Cuk斩波电路的双向双层桥臂结构均衡电路的控制策略。
分析蓄电池不均衡的状态,主要分为以下三种情况[30]:
(1)只有个别电池的SOC较高;
(2)只有个别电池的SOC较低;
(3)各个电池的SOC参差不齐。
依据以上三种蓄电池不同的不平衡状态,设计了相应的控制策略。
情况1:直接将SOC较高的电池通过双层桥臂接入到主均衡电路中,将能量转移给外部辅助均衡蓄电池。
情况2:直接将SOC较低的电池通过双层桥臂接入到主均衡电路中,从外部辅助均衡蓄电池吸收电能。
情况3:将单体蓄电池SOC与平均SOC进行比较,优先对偏离程度大的蓄电池进行均衡。
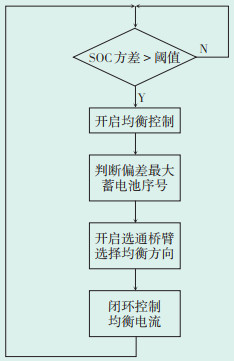
只有蓄电池组的SOC不平衡度达到一定程度时,才开始进行均衡控制。本文根据SOC的方差不平衡程度而开启均衡控制[35-37]。均衡控制策略流程如图 4所示。
|
| 图 4 均衡控制策略流程 Figure 4 Balanced control strategy flow chart |
二阶RC等效电路模型的端电压表达式为:
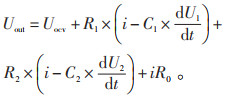
|
(23) |
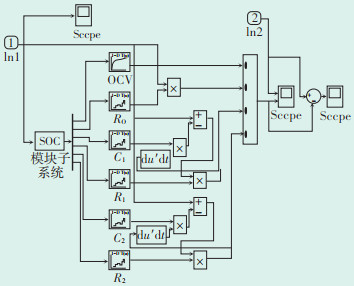
使用Simulink验证电池模型的可靠性、精度和参数辨识的准确性,电池模型如图 5所示。将OCV-SOC和参数辨识的结果R0、R1、R2、C1、C2输入到6个模块,输入HPPC实验中所记录的电流数据,可以得到如式(23)所示开路电压。使用该开路电压与实验中所采集到的电压进行对比,并使用示波器(Scope)进行观察即可判断电池模型选取的精度和参数辨识的效果。
|
| 图 5 电池模型等效电路 Figure 5 Battery model equivalent circuit |
其中,左边的模块子系统是为了得到当前SOC的真实值。通过HPPC实验,设定充电截止时刻为S=1,放电截止为S=0。其间的SOC值,根据HPPC实验过程中所采集到的电流使用安时积分法进行计算,采集电流的精度为1 mA。
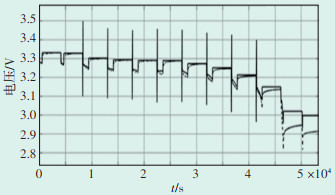
导入HPPC实验记录的数据和参数辨识结果,判断电池模型和参数辨识的准确性,对比结果如图 6所示。
|
| 图 6 实验电压与电池模型电压 Figure 6 Experimental voltage and battery model voltage 图中:····—实验电压;———模型电压。 |
在SOC位于20%~100%,通过辨识的参数计算得到蓄电池开路电压,能够很好地和实验采集到的电压贴合。但当SOC在20%及以下时,计算得到的开路电压与实际采集到的开路电压并不符合,可能因为蓄电池在较低SOC的性能太差,导致参数辨识不准确。
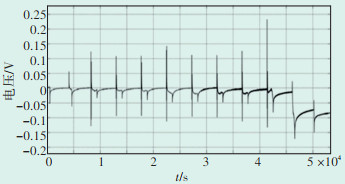
图 7为HPPC实验中采集到的电压与使用二阶RC电池模型估计的电压之差。在每个HPPC实验阶段两者都会产生一个较大偏差,其中最大偏差约为0.23 V。但在HPPC实验阶段后,电池模型得到的电压能够马上趋近实验电压,误差在0.02 V以内。当SOC在20%以下时,偏差较大,HPPC实验阶段的最大误差为0.17 V,实验后的误差在0.1 V以内。可能因为在较低SOC时,蓄电池性能较差,导致电池模型的参数估计不准确。总体而言,选取的二阶RC电池等效电路模型具有较高的精度,参数辨识的结果较好。
|
| 图 7 实验电压与电池模型电压之差 Figure 7 Difference between experimental voltage and battery model voltage |
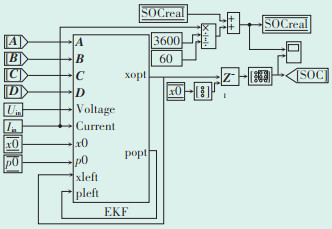
基于EKF方法,电池SOC初始值的设定主要包含了3个部分:状态变量的初始值,协方差矩阵的初始值,过程噪声和测量噪声的方差。图 8为EKF算法估计电池SOC仿真电路模型。图中A、B、C、D为4个随SOC更新的系数矩阵,EKF估计SOC的初始值包括状态变量初始值x0和协方差矩阵初始值p0。输入控制量Iin和观测量Uin,并将更新的系数矩阵输入EKF估计SOC中。在右侧分别对真实SOC和使用EKF估计得到的SOC搭建观察部分。
|
| 图 8 EKF估计SOC仿真电路模型 Figure 8 EKF estimation SOC simulation circuit model |
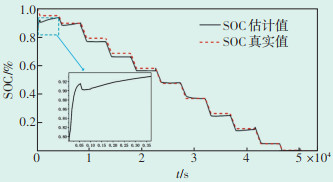
SOC估计差初始值设定为50%,而真实SOC为100%,偏差为50%,电池SOC估计值能够很快的跟踪上电池SOC真实值,如图 9所示。使用EKF算法在电池SOC 0~100%变化时对SOC进行估计,其最大偏差为2.5%,因此所用EKF算法精度较高,满足要求。
|
| 图 9 SOC估计仿真跟踪图 Figure 9 SOC estimation simulation tracking diagram |
应用Simulink仿真软件搭建基于Cuk的双向双层桥臂结构的均衡电路,应用图 4的控制策略对各个电池单体均衡电流进行控制。根据该仿真设计,进行控制策略的仿真验证及分析。
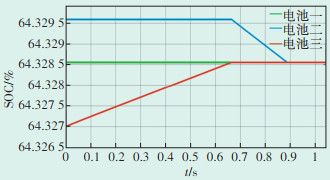
给定各单体蓄电池额定容量60 Ah,额定电压3.3 V。为了能够较快得到结果,设定初始SOC分别为64.328 55%、64.329 6%、64.327%。设置串联蓄电池组的充电均衡电流为5 A,放电均衡电流为10 A。
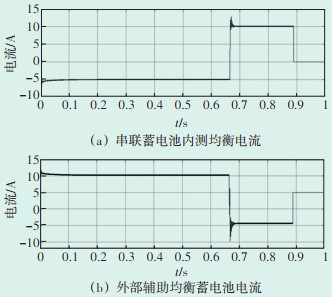
三节蓄电池进行控制策略仿真验证的SOC曲线如图 10所示。第一节电池的SOC处于中间,所以统一将其他电池的SOC均衡至第一节电池的SOC。第三节电池SOC初始值与第一节的偏差,大于第二节电池SOC初始值与第一节的偏差,所以优先对第三节电池进行均衡控制。因为第三节电池SOC小于第一节电池SOC,所以执行充电均衡,充电电流为设置的5 A。当第三节电池SOC等于第一节时,开始对第二节电池进行放电均衡,放电电流为设置的10 A。蓄电池均衡电流波形如图 11所示。
|
| 图 10 均衡策略仿真SOC波形 Figure 10 Equalization strategy simulation SOC waveform |
|
| 图 11 均衡策略仿真电流 Figure 11 Equalization strategy simulation current |
硬件实验平台主要分为串联蓄电池组、Cuk均衡主电路、采样电路、双层桥臂选通电路和DSP控制。硬件平台实物如图 12所示。

|
| 图 12 硬件平台实物图 Figure 12 Hardware platform physical map |
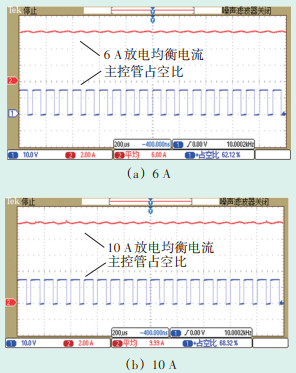
首先对蓄电池组进行放电均衡,分别设置放电电流参考值为6 A、10 A,实现放电均衡电流控制。其次对蓄电池组进行充电均衡,分别设置充电参考电流值为3 A、5 A,实现充电均衡电流控制。图 13为放电均衡的6 A、10 A的蓄电池放电电流波形和对应主控制管的占空比。
|
| 图 13 放电均衡6 A、10 A放电电流波形及对应主控管占空比 Figure 13 Discharge equalization 6 A and 10 A current waveform and the corresponding duty cycle of the main control tube |
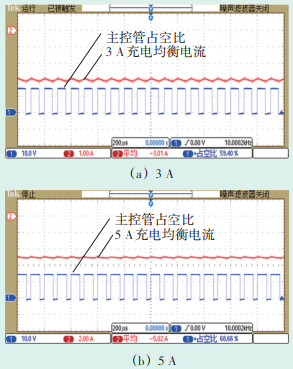
图 14为充电均衡3 A和5 A的蓄电池充电电流波形及对应主控管的占空比。
|
| 图 14 充电均衡3 A、5 A充电电流波形及对应主控管占空比 Figure 14 Charging equalization 3 A and 5 A current waveform and the corresponding duty cycle of the main control tube |
图 15为放电、充电均衡时蓄电池放电充电电流的启动调节过程。放电均衡的蓄电池放电电流为10 A,充电均衡的蓄电池充电电流为5 A。其中,信号3为辅助均衡蓄电池电流,信号4为串联蓄电池组中进行均衡控制的蓄电池电流。

|
| 图 15 放电、充电均衡电流启动调节过程 Figure 15 Starting and adjusting process of discharge and charge equalization current |
从图 15可以看出,无论是放电均衡还是充电均衡都能够在3 s达到稳定状态,可以快速实现均衡电流的控制。
5 结语本文对串联蓄电池组进行了均衡电流控制,以SOC作为均衡依据,使用二阶RC等效电路模型,通过HPPC实验进行参数辨识,仿真验证基于EKF估计SOC,SOC估计的最大误差为2.5%。选用基于Cuk斩波电路的双向双层桥臂均衡电路,制定了均衡电流控制策略,并在硬件实验平台上得到验证。本文提出的方法能够实现电流均衡,并且均衡损耗小,蓄电池组均衡速度显著提高。
| [1] |
戴海峰, 王楠, 魏学哲, 等. 车用动力锂离子电池单体不一致性问题研究综述[J].
汽车工程, 2014, 36(2)181-188, 203 DAI Haifeng, WANG Nan, WEI Xuezhe, et al. A Research Review on the Cell Inconsistency of Li-ion Traction Batteries in Electric Vehicles[J]. Automotive Engineering, 2014, 36(2)181-188, 203 DOI:10.3969/j.issn.1000-680X.2014.02.011 (  0) 0)
|
| [2] |
黄莉莉, 任星星, 苗博博, 等. 基于改进Rint模型锂离子电池SOC估计[J].
电池工业, 2022, 26(4): 177-180 HUANG Lili, REN Xingxing, MIAO Bobo, et al. SOC Estimation of Lithium-Ion Battery Based on Rint Model[J]. Chinese Battery Industry, 2022, 26(4): 177-180 DOI:10.19996/j.cnki.ChinBatlnd.2022.04.004 (  0) 0)
|
| [3] |
徐东辉. 锂电池一阶RC等效电路模型的动力学特性分析[J].
电源技术, 2021, 45(11): 1448-1452 XU Donghui. Dynamic Analysis of First-order RC Equivalent Circuit Model for Automotive Lithium Ion Power Batteries[J]. Chinese Journal of Power Sources, 2021, 45(11): 1448-1452 DOI:10.3969/j.issn.1002-087X.2021.11.018 (  0) 0)
|
| [4] |
刘冬雷, 范永存, 王顺利, 等. 基于RFMRA和改进PNGV模型的锂离子电池SOC估算[J].
电池, 2021, 51(5): 470-473 LIU Donglei, FAN Yongcun, WANG Shunli, et al. Estimation of Li-ion Battery SOC Based on RFMRA and Improved PNGV Model[J]. Battery Bimonthly, 2021, 51(5): 470-473 DOI:10.19535/j.1001-1579.2021.05.008 (  0) 0)
|
| [5] |
汪贵芳, 王顺利, 于春梅. 结合Thevenin和PNGV模型的电池等效电路建模改进[J].
自动化仪表, 2021, 42(2)45-49, 55 WANG Guifang, WANG Shunli, YU Chunmei. Improvement of Battery Equivalent Circuit Modeling Combined with Thevenin and PNGV Models[J]. Process Automation Instrumentation, 2021, 42(2)45-49, 55 DOI:10.16086/j.cnki.issn1000-0380.2019070048 (  0) 0)
|
| [6] |
郭玉威. 基于GNL模型自适应无迹卡尔曼滤波的电池荷电状态估计[D]. 北京: 华北电力大学, 2019.
(  0) 0)
|
| [7] |
杜森, 谢立洁, 徐梓荐, 等. 三阶扩展GNL电池模型的研究[J].
电子设计工程, 2018, 26(20)110-113, 118 DU Sen, XIE Lijie, XU Zijian, et al. Research on Three Level Expanded GNL Cell Module[J]. Electronic Design Engineering, 2018, 26(20)110-113, 118 DOI:10.3969/j.issn.1674-6236.2018.20.024 (  0) 0)
|
| [8] |
冷炎. 基于CKF的锂电池SOC估算及其电池管理系统研究[D]. 镇江: 江苏大学, 2016.
(  0) 0)
|
| [9] |
刘迪, 李琳, 姜晓健. 基于安时积分法和UKF的锂电池SOC估测[J].
新型工业化, 2021, 11(11): 125-128 LIU Di, LI Lin, JIANG Xiaojian. SOC Estimation of Li-Ion Batteries Based on Ampere-time Integration Method and UKF[J]. The Journal of New Industrialization, 2021, 11(11): 125-128 (  0) 0)
|
| [10] |
申彩英, 左凯. 基于开路电压法的磷酸铁锂电池SOC估算研究[J].
电源技术, 2019, 43(11): 1789-1791 SHEN Caiying, ZUO Kai. Research on SOC estimation of LiFePO4 Batteries Based on Open Circuit Voltage Method[J]. Chinese Journal of Power Sources, 2019, 43(11): 1789-1791 (  0) 0)
|
| [11] |
孙艳艳, 周雪松, 游祥龙, 等. 基于开路电压法的电池荷电状态估算修正[J].
内燃机与配件, 2019(19): 225-226 SUN Yanyan, ZHOU Xuesong, YOU Xianglong, et al. Correction of Battery Charge State Estimation Based on Open Circuit Voltage Method[J]. Internal Combustion Engine & Parts, 2019(19): 225-226 DOI:10.3969/j.issn.1674-957X.2019.19.114 (  0) 0)
|
| [12] |
续远. 基于安时积分法与开路电压法估测电池SOC[J].
新型工业化, 2022, 12(1)123-124, 127 XU Yuan. Estimation of Battery SOC Based on Ampere-time Integration and Open-circuit Voltage Method[J]. The Journal of New Industrialization, 2022, 12(1)123-124, 127 (  0) 0)
|
| [13] |
王绍远, 胡斌, 王良秀, 等. 基于卡尔曼滤波法的船用磷酸铁锂电池SOC仿真估算[J].
船舶工程, 2022, 44(2): 89-93 WANG Shaoyuan, HU Bin, WANG Liangxiu, et al. Simulation of SOC for Marine LiFePO4 Battery Based on Kalman Filter[J]. Ship Engineering, 2022, 44(2): 89-93 (  0) 0)
|
| [14] |
黄英. 卡尔曼滤波法估算电池系统荷电状态[J].
汽车实用技术, 2021, 46(11): 6-9 HUANG Ying. Estimating the State of Charge of a Battery System by Kalman Filter Method[J]. Automobile Technology, 2021, 46(11): 6-9 (  0) 0)
|
| [15] |
LI Zheng, ZHANG Liping, ZHANG Rui, et al. Unscented Kalman filtering method for scheduling photovoltaic power generation system fluctuations[J].
Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2021, 235(3): 608-619 (  0) 0)
|
| [16] |
王党树, 王新霞. 基于扩展卡尔曼滤波的锂电池SOC估算[J].
电源技术, 2019, 43(9): 1458-1460 WANG Dangshu, WANG Xinxia. SOC estimation of lithium-ion battery based on extended Kalman filter[J]. Chinese Journal of Power Sources, 2019, 43(9): 1458-1460 (  0) 0)
|
| [17] |
杨学平, 王正江, 蒋超宇, 等. 基于BP神经网络法研究锂电池荷电状态[J].
材料导报, 2019, 33(S2): 53-55 YANG Xueping, WANG Zhengjiang, JIANG Chaoyu, et al. State of Charge of Lithium-Ion Battery Based on BP Neural Network[J]. Materials Reports, 2019, 33(S2): 53-55 (  0) 0)
|
| [18] |
LIU Xiaojing, DAI Yawen. Energy storage battery SOC estimate based on improved BP neural network[J].
Journal of Physics: Conference Series, 2022: 2187 (  0) 0)
|
| [19] |
曹弘飞, 朱新坚. BP神经网络在线优化卡尔曼滤波算法在钒电池SOC估算中的应用[J].
电力建设, 2018, 39(4): 9-14 CAO Hongfei, ZHU Xinjian. Application of Online Optimized Kalman Filter using BP Neural Network on SOC Estimation of Vanadium Redox Flow Battery[J]. Electric Power Construction, 2018, 39(4): 9-14 (  0) 0)
|
| [20] |
孙志浩. 动力电池主动均衡技术的研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
(  0) 0)
|
| [21] |
李素平, 许明坤, 唐瑞华. 一种多电容拓扑结构的均衡电路设计与仿真[J].
电子世界, 2019(14): 15-17 LI Suping, XU Mingkun, TANG Ruihua. Design and Simulation of an Equalisation Circuit with a Multi-Capacitor Topology[J]. Electronics World, 2019(14): 15-17 (  0) 0)
|
| [22] |
王慧娴. 串联蓄电池组均衡电流定量控制策略的研究[D]. 北京: 北方工业大学, 2017.
(  0) 0)
|
| [23] |
宫茗宣. 锂离子电池SOC估算及变电流均衡控制研究[D]. 大连: 大连海事大学, 2020.
(  0) 0)
|
| [24] |
严志星, 曾君, 赖臻, 等. 一种基于内置变压器的高增益双向DC-DC变换器[J].
电源学报, 2020, 18(3): 4-12 YAN Zhixing, ZENG Jun, LAI Zhen, et al. High voltage-gain bidirectional DC-DC converter based on built-in transformer[J]. Journal of Power Supply, 2020, 18(3): 4-12 (  0) 0)
|
| [25] |
梁中会, 李宁, 韩兴旺, 等. 一种基于开关电容的电池串均衡电路[J].
电力电子技术, 2021, 55(8)28-30, 35 LIANG Zhonghui, LI Ning, HAN Xingwang, et al. A Battery Strings Equalizer Circuit Based on Switching Capacitance[J]. Power Electronics, 2021, 55(8)28-30, 35 (  0) 0)
|
| [26] |
Yarlagadda S., Hartley T. T., Husain I.. A Battery Management System Using an Active Charge Equalization Technique Based on a DC/DC Converter Topology[J].
IEEE Transactions on Industry Applications, 2013, 49(6): 2720-2729 (  0) 0)
|
| [27] |
范元亮, 吴涵, 徐梦然, 等. 一种混合开关电容和开关电感的新型均衡电路[J].
电工电能新技术, 2021, 40(6): 57-63 FAN Yuanliang, WU Han, XU Mengran, et al. A Novel Equalization Circuit Combining Switched-Capacitor and Switched-Inductor[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(6): 57-63 (  0) 0)
|
| [28] |
杨坚, 张巧杰, 赵旭. 电池组改进型电感均衡电路研究[J].
传感器世界, 2018, 24(1): 19-24 YANG Jian, ZHANG Qiaojie, ZHAO Xu. Improved Inductance Equalization Circuit for Battery Pack[J]. Sensor World, 2018, 24(1): 19-24 (  0) 0)
|
| [29] |
梁嘉羿, 王友仁, 黄薛, 等. 蓄电池能量均衡技术研究综述[J].
机械制造与自动化, 2018, 47(3): 26-30 LIANG Jiayi, WANG Youren, HUANG Xue, et al. Research Status of Balancing Technique for Series Connected Battery[J]. Machine Building & Automation, 2018, 47(3): 26-30 (  0) 0)
|
| [30] |
何俊儒, 王洪诚, 方余丞, 等. 基于CUK双向变换器的串联电池均压法[J].
蓄电池, 2016, 53(1): 26-30 HE Junru, WANG Hongcheng, FANG Yucheng, et al. Equalizing method for series-connected battery based on CUK bidirectional converter[J]. Chinese LABAT Man, 2016, 53(1): 26-30 (  0) 0)
|
| [31] |
粟渊恺, 冯骞, 粟时平, 等. H桥链式STATCOM直流电容电压稳定与均衡控制[J].
电力电子技术, 2021, 55(6): 13-18 SU Yuankai, FENG Qian, SU Shiping, et al. DC capacitor voltage stability and equalization control of H-bridge cascaded STATCOM[J]. Power Electronics, 2021, 55(6): 13-18 (  0) 0)
|
| [32] |
Engineeringlaboratory EIN. FreedomCAR Battery Test Manual For Power-Assist Hybrid Electric Vehicles[M/OL]. [2012-06-04]. http://www.doc88.com/p-680406055857.html.
(  0) 0)
|
| [33] |
曹丽鹏, 谢阳, 李玲玲, 等. 锂离子电池等效电路模型及参数辨识方法研究[J].
电气时代, 2017(2): 85-87 CAO Lipeng, XIE Yang, LI Lingling, et al. Equivalent circuit model and parameter identification method for Lithium-Ion batteries[J]. Electric Age, 2017(2): 85-87 (  0) 0)
|
| [34] |
王骏骏. 基于ICS-LSSVM的电动汽车锂电池SOC预测[J].
东北电力技术, 2022, 43(12): 52-56 WANG Junjun. SOC Prediction of Electric Vehicle Lithium Battery Based on ICS-LSSVM[J]. Northeast Electric Power Technology, 2022, 43(12): 52-56 (  0) 0)
|
| [35] |
宋绍剑, 王志浩, 林小峰. 基于SOC的锂动力电池组双向主动均衡控制[J].
系统仿真学报, 2017, 29(3): 609-617 SONG Shaojian, WANG Zhihao, LIN Xiaofeng. SOC-Based Bi-Directional Active Equalization Control for Lithium-Ion Power Battery[J]. Journal of System Simulation, 2017, 29(3): 609-617 (  0) 0)
|
| [36] |
欧阳剑, 李迪, 柳俊城. 电动汽车用动力电池荷电状态估算方法研究综述[J].
机电工程技术, 2016, 45(1): 52-56 OUYANG Jian, LI Di, LIU Juncheng. The Overview of Research of Power Battery SOC Estimation Methods Use for Electric Vehicle[J]. Mechanical & Electrical Engineering Technology, 2016, 45(1): 52-56 (  0) 0)
|
| [37] |
原帅, 王悦, 李超. 电动汽车动力电池运行中SOC性能评估分析[J].
内蒙古电力技术, 2016, 34(6): 81-84 YUAN Shuai, WANG Yue, LI Chao. SOC Performance Evaluation Analysis in Electric Vehicle Power Battery Operation[J]. Inner Mongolia Electric Power, 2016, 34(6): 81-84 (  0) 0)
|
 2023, Vol. 41
2023, Vol. 41

