0 引言

随着我国经济的快速发展，煤炭、石油等传统能源已无法满足社会的需求，且资源枯竭、气候变化及环境破坏等问题日益凸显。2020年9月，我国提出双碳目标，各区域电网充分响应，新能源发电占比不断增加^[1-4]。然而，新能源发电普遍具有随机性和波动性^[5-6]等问题，导致电网的灵活性需求显著升高^[7-9]。同时，当今电网的可调节资源种类繁多，约束条件各不相同，求解最优的可调节资源调度方案运算复杂、耗时长，随着未来可调节负荷的大量接入，定量分析与协同控制变得十分困难^[10-11]。针对这一问题，目前常用方法是事先对各类可调节资源进行层级评估，在调用过程中根据层级从高到低依次调用可调节资源，可在实际应用过程中加速计算。

如何对可调节资源进行评估是电网中的关键问题，国家能源局东北监管局、华东监管局、华北监管局等发布的《并网运行管理实施细则》重点关注自动功率控制（Auto Power Control，APC），从可用率考核和性能考核两个角度对除可调节负荷外的各类可调节资源的评估方式提出了要求。部分学者重点关注快速发展的新型可调节资源，结合其单日可响应次数有限、可连续响应时间有限的特点，提出了对可调节负荷的评估方法^[12-14]，但是该方法并未将可调节负荷与其他可调资源共同进行评估。部分学者在评估过程中引入聚类方法^[15-16]，对一种资源从多方面进行评估，使得结果具有多方面可参考性，但资源种类较少。

本文提出了一种基于K-means++聚类算法的多类型可调节资源容量特性层级评估方法，在可靠性、灵活性的基础上还引入了经济性指标，对各类型可调节资源的调频和调峰两类典型调节能力进行评估，保证了对包括可调节负荷在内的各类可调节资源采用同一尺度、同一公式，确保了评估结果的可参考性，再对评估结果使用改进K-means++聚类方法进行聚类，最后根据各个簇的聚类中心确定可调节资源所属层级，实现对多类型可调节资源的层级评估。

1 可调节资源评估方法 1.1 调频能力评估方法

《华北区域电力并网运行管理实施细则》中对各类可调节资源参与APC的调节性能评估公式见式（1）：

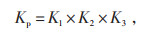
(1)

式中：K_p—调节性能综合指标；

K₁—可调节资源调节速率指标；

K₂—可调节资源调节精度指标；

K₃—可调节资源响应时间指标。

在计算过程中对K₁、K₂、K₃三项均有上下限要求，当小于0.1时取0.1，大于1.5时取1.5。

该指标只适用于除可调节负荷以外的其他可调节资源，未考虑可调节负荷单位时间内可响应次数有限的问题。此外，由于该指标主要目的是对可调节资源参与APC的考核，仅关注可靠性、灵活性等性能指标，对可调节资源的经济性特征没有考虑。

本文中评估指标的主要目的是使用指标计算结果进行层级评估，为保证层级评估结果考虑的因素齐全、结果可靠，在可调节资源的可靠性、灵活性的基础上对经济性也进行考量，当某一可调节资源经济性较差时，需降低其评级。基于上述分析，本文提出一种可调节资源调频能力的评估方法，见式（2）。

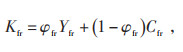
(2)

式中：K_fr—考虑经济性的调频综合指标；

φ_fr—常数系数，满足φ_fr∈（0，1）；

Y_fr—调频综合指标，包括可靠性和灵活性两个方面；

C_fr—调频经济性指标。

式中，Y_fr与C_fr采取加权求和而不是相乘的计算方法得到K_fr，不赋予经济性指标C_fr一票否决权，防止新型储能等高可靠性、强灵活性、低经济性的可调节资源评估结果过差。

Y_fr的表达式见式（3），C_fr的表达式见式（4）。

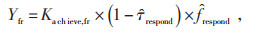
(3)

式中：K_{a ch ieve, fr}—成功响应率，为成功响应次数与总调用次数的比值；

—响应时间归一值；

—响应频率归一值。

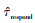
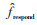
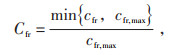
(4)

式中：c_fr—可调节资源调频成本；

c_{fr, max}—可调节资源调频成本上限值。

式（3）中，K_{a ch ieve, fr}体现对可调节资源调节可靠性的评价，和 体现对灵活性的评价。式（3）参考式（1），不同变量之间采用乘法计算，赋予每项指标对Y_fr的一票否决权，任意一项指标过低均可以导致综合指标Y_fr显著偏差。由于本文提出的可调节资源评估是一种在调度之前的事先评估，可调节功率会随具体的运行状态而变化，因此不对调节速率K₁进行考量，并将单次调节的调节精度K₂替换为具有统计性的成功响应率K_{a ch ieve, fr}。考虑到可调节负荷单位时间内可响应次数有限，引入响应频率归一值来反映其可响应能力，该数值越低代表可调用次数越少、响应能力越差，对于响应次数不受限制的可调节资源，该项取1，由此实现了对可调节负荷和其他可调节资源采用同一评价尺度进行评估，避免了不同类型可调节资源因为评估标准不同而导致的评估结果存在差异的问题，保证了评估结果的一致性，可为层级评估提供可靠依据。

1.2 调峰能力评估方法

针对调峰场景，本文提出的可调节资源调峰能力评估方法与调频能力的评估方法类似，具体见式（5）。

(5)

式中：K_ps—考虑经济性的调频综合指标；

φ_ps—常数系数，满足φ_ps∈(0, 1)；

Y_ps—调峰综合指标，包括可靠性和灵活性两个方面；

K_{a ch ieve, ps}—成功响应率，为成功响应次数与总调次数的比值；

C_ps—调峰经济性指标；

—可连续响应时间归一值；

c_ps—可调节资源调峰成本；

c_{ps, max}—可调节资源调峰成本上限值。

K_ps的计算方式与K_fr类似，主要在对可调节负荷的处理方式有一定差异。在调频能力评估中，重点关注可调节负荷单位时间内可响应次数有限的特征，在调峰能力评估中则重点关注其可连续响应的时间有限的问题。因此，使用可连续响应时间归一值取代响应频率归一值；与类似，对于可连续响应时间不受限制的可调节资源取1。

2 基于改进K-means++聚类的层级评估 2.1 基于改进K-means++聚类的层级划分方法

由前述可知，可调节资源存在种类多、优化求解算例要求高的问题，因此可以考虑事先对可调节资源的调节能力进行层级划分。本文对层级划分的定义如下：针对由数个可能存在互有影响的因素所得出的评价结果，使用某种算法对评价结果进行评级分层的过程。通过层级划分，可以有效降低由于交叉影响的权重因子对评估结果的潜在影响。本文中的因素包括综合指标和经济性指标。

在众多的聚类方法中，本文选择K-means++聚类，该方法作为经典聚类算法，具有复杂度低、聚类效果好等特点，同时K-means++聚类确定了具体的聚类中心初值，解决了K-means聚类中同一样本不同次数聚类结果不同的问题，增加了聚类结果的稳定性^[17-19]。

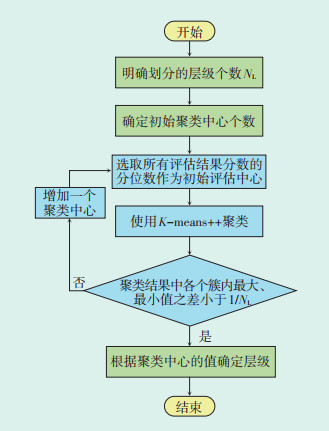
本文所提出的基于改进K-means++聚类的层级划分流程图如图 1所示。

首先，明确要划分的层级个数N_L。其次，确定初始的聚类中心个数。再次，使用评估结果的分位数作为初始的评估中心进行K-means++聚类，如果聚类结果中存在某个簇的最大、最小值之差大于1/N_L，则增加一个聚类中心重新进行聚类，直至各个簇中的最大、最小值之差均小于1/N_L为止。最后，根据聚类中心的值确定层级。在层级确定过程中分别计算各个可调节资源的调频能力层级以及调峰能力层级。

在经典的K-means++聚类中，由于是将最相近的几个样本划入同一个簇中，容易出现不同簇的最大、最小值差之间差异巨大的现象，如图 2所示。图 2中簇1中的最大、最小值差明显大于簇3中的最大、最小值差，该聚类结果没有完成对簇1中的各项进行有效区分，导致簇1中的各项可调资源所划分的层级可参考性差。为处理上述问题，本文提出了改进K-means++聚类，该方法相较于经典的K-means++聚类增加了一个对各个簇内最大、最小值之差的判断，如果簇内最大、最小值差大于预设的层级范围1/N_L时，则增加一个聚类中心再次进行聚类。这种不断补充聚类中心的过程既保证了对各项都进行了有效区分，又避免了K-means聚类中普遍存在的聚类中心个数不易确定的问题。

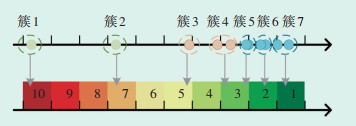
在获得有效的聚类结果后，根据各个簇的聚类中心确定其所在的层级。对于聚类中心C，总存在层级j使得C∈[(N_L-j)/N_L, (N_L-j + 1)/N_L]，则认为C是j层，j越小层级越高，代表其调节能力越强。仍以图 2中的各个点为例，使用改进K-means++聚类后在层级个数N_L=10的场景下层级划分结果如图 3所示。在改进K-means++聚类中，通过增加聚类中心个数，实现了对各个簇的有效区分。同时，从簇4和簇5可以看出，增加聚类中心可能会导致聚类中心个数出现冗余，但经过依照聚类中心值确定所属层级，簇4和簇5虽然聚类结果不属于同一个簇，但是依照其聚类中心的值划入同一层，聚类中心冗余的问题不会对层级划分的结果产生影响。

2.2 多类型可调节资源层级评估

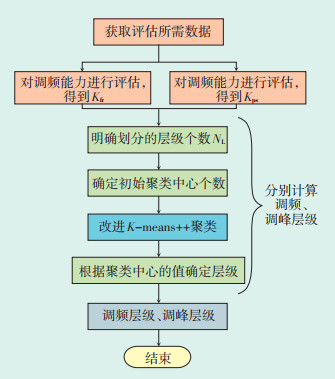
综合上述方法，最终确定多类型可调节资源层级评估方法，其流程图如图 4所示。

3 算例分析 3.1 可调节资源调频能力层级评估

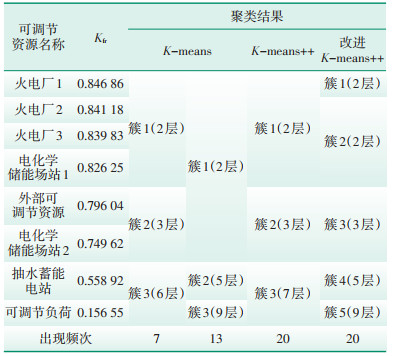
以北方某高比例新能源接入地区电网为例，对其内部可调节资源的调频特性进行评估。φ_fr取0.67，即可靠性、灵活性、经济性给予相等的权重，c_{fr, max}取2000元/MW，N_L取10。经过计算评分结果以及层级评估结果如表 1所示（已按照K_fr降序排序）。为对比所提出的改进K-means++聚类的性能，在本算例中，分别使用K-means聚类、K-means++聚类、改进K-means++聚类以3为初始聚类中心个数对评估结果聚类20次。

对比表 1中各类型聚类算法聚类结果可以发现，改进K-means++算法相较于K-means算法具有运算稳定性，聚类结果唯一；相较于K-means++算法则能够对抽水蓄能电站和可调节负荷这两类资源的层级进行有效划分，而不是放入同一个层级中。

关注K-means++聚类及改进K-means++聚类的结果可以发现，K-means++聚类的结果中簇1最大、最小值差为0.020 61，簇2最大、最小值差为0.046 42，簇3最大、最小值差为0.402 37，簇3内最大、最小值差远大于簇1和簇2中的值，聚类结果没有对簇3中的两类资源做出有效区分。反映在评级上，抽水蓄能电站和可调节负荷都被划入了7级，即（0.3，0.4]中，为二者的平均值所在范围。而在改进K-means++聚类中，8类可调节资源被聚类到5个簇，对抽水蓄能电站和可调节负荷做出有效区分，分别列于5级和9级。

仅关注改进K-means++聚类结果可以发现，簇1和簇2被归入同一个层级中，即聚类中心中存在冗余，并通过按照聚类中心确定层级的方式避免了冗余对层级评估结果的影响。

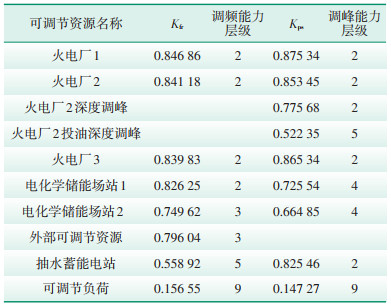
3.2 可调节资源调频调峰能力层级评估

仍以3.1节中高比例新能源接入地区为例，分别对地区内可调节资源的调频能力以及调峰能力进行层级评估。在评估过程中，认为外部可调节资源不参与调峰，深度调峰、投油深度调峰不参与调频，调频相关参数设置与3.1节相同，此外，调峰相关参数中φ_ps取0.67，c_{ps, max}取1000元/MWh。评估结果如表 2所示。从表 2可以看出，对于该评估地区，本文提出的评估方法可以有效做出层级评估。在调频方面，抽水蓄能电站表现不如电化学储能场站；在调峰方面，抽水蓄能电站表现强于电化学储能电站。由于存在响应频率、连续响应时间等方面的限制，且成本较高，可调节负荷在调频和调峰场景的层级评估都较差。对于火电厂，其深度调峰能力略优于电化学储能的调峰能力，但是在当期处于投油深度调峰状态下，由于调峰成本的显著升高，其调峰能力劣于电化学储能场站。

4 结束语

本文提出一种基于改进K-means++聚类的多类型可调节资源层级评估方法，针对不同类型的可调节资源从可靠性、灵活性、经济性角度建立了具有相同计算方式的调频能力、调峰能力评估指标，将多类型可调节资源从相同尺度进行评估；引入了聚类思想，通过聚类结果的聚类中心值进行层级划分，解决了固定数值作为层级分界线导致性能相近的可调节资源被分入不同层级的问题，增加了层级评估结果的可靠性；提出改进K-means++聚类，通过动态增加聚类中心，保证了聚类算法对各项元素都进行有效区分，并通过算例分析证明了本次改进的有效性；最后以北方某地区为算例，对本文提出的基于改进K-means++聚类的多类型可调节资源层级评估进行了验证，证明了所提出层级评估方法在调频能力、调峰能力评估方面的有效性。