2. 国网湖北省电力有限公司荆门供电公司,湖北 荆门 448000;
3. 三峡大学电气与新能源学院,湖北 宜昌 443000
2. Jingmen Power Supply Company, State Grid Hubei Electric Power Co., Ltd., Jingmen 448000, China;
3. College of Electrical and New Energy, Three Gorges University, Yichang 443000, China
在能源危机和全球变暖的大背景下,近些年风力发电总量一直保持高速增长的态势,截至2022年底,全球风电累计装机容量高达898 824 MW。风力发电不消耗化石能源,也不会产生污染气体,大力推广风力发电能够减少碳排放量,进而缓解能源危机[1-5]。但风电功率的随机性和波动性较大,在并网过程中会改变配电网潮流分布,影响电压质量[6-9]。因此,对含风电配电网无功优化进行分析研究,对于改善电压质量和提高电力系统稳定性具有重要意义[10-12]。
为了减小风电接入对配电网电能质量和稳定性的影响,国内外学者对含风电配电网无功优化进行了大量研究。文献[5]将风电作为间歇式分布式能源的代表,以配电网网损和电压偏差最小为优化目标,采用改进粒子群算法对优化目标进行求解,建立了基于改进粒子群算法的配电网无功优化模型。文献[6]采用概率场景分析法对风电出力不确定性进行了处理,建立了基于自适应网格多目标粒子群算法的含风电配电网无功优化模型,采用风电接入的IEEE33节点系统对模型的正确性进行了验证。文献[7]建立了包含有功网络损耗成本、静态电压稳定成本和无功补偿投资成本等各项成本的含风电配电网无功优化模型,采用二次变异改进的差分算法对模型进行了求解,验证了模型的正确性和改进方法的有效性。含风电配电网结构复杂,现有模型的目标函数和约束条件有待进一步完善,模型的求解方法也有待进一步研究。
本文建立以配电网节点电压总偏移指数最小为目标函数的含风电配电网无功优化模型,采用改进狼群算法(Improved Wolf Pack Algorithm,IWPA)对模型进行求解,并利用灵敏度分析确定无功补偿位置,采用算例分析对模型的正确性和求解方法的有效性进行验证。
1 配电网无功优化数学模型 1.1 目标函数在对配电网进行无功优化时,首端节点、无功电压分布等参数均会引起配电网电压和网损的变化,为了提高配电网电压质量,应首先保证配电网节点电压的稳定性。本文以配电网节点电压总偏移指数最小作为目标函数,具体如下:
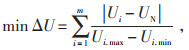
|
(1) |
式中:Ui为节点i的电压幅值;UN为配电网额定电压基准值;Ui. max和Ui. min分别为节点i的最大电压幅值和最小电压幅值;m为节点数量。
1.2 约束条件(1)功率平衡约束:
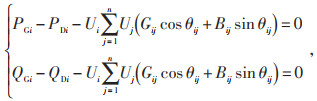
|
(2) |
式中:PGi为节点i注入的有功功率;PDi为节点i的有功负荷;QGi为节点i注入的无功功率;QDi为节点i的无功负荷;Gij为节点i和节点j之间的电导;Bij为节点i和节点j个之间的电纳;θij为节点i和节点j之间的电压相位差;n为配电网支路数。
(2)节点电压幅值约束:
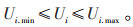
|
(3) |
(3)无功补偿容量约束:
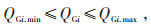
|
(4) |
式中:QGi为节点i的动态无功补偿发生装置(Static Var Generator,SVG)无功补偿功率;QGi. min为节点i的SVG无功补偿功率的最小值;QGi. max为节点i的SVG无功补偿功率的最大值。
(4)风电出力约束:
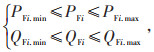
|
(5) |
式中:PFi为节点i的有功输出功率;PFi. max为风电最大有功输出功率;PFi. min为风电最小有功输出功率;QFi为节点i的无功输出功率;QFi. max为风电最大无功输出功率;QFi. min为风电最大有功输出功率。
2 无功补偿点选取风电接入配电网后会引起潮流变化,为了减小风电接入的影响,需要对配电网系统进行无功补偿,本文采用灵敏度分析方法[8]确定无功补偿节点的位置,灵敏度分析的具体实施策略是:根据各节点无功变量注入造成系统网损的优劣顺序,排名靠前的节点灵敏度较高,灵敏度高的节点就是需要进行无功补偿的节点。
配电网有功损耗Ploss可表示为:
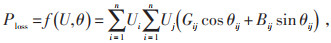
|
(6) |
式中:U为配电网电压;θ为电压相位差。
对式(6)求偏导,可得配电网各节点无功变化与系统网损的灵敏度关系如下:
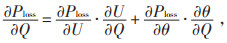
|
(7) |
式中:Q为配电网无功功率。
为了得到式(7),需要进行如下变化:
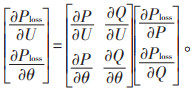
|
(8) |
对式(8)进行变化后可得到Jacobi矩阵:
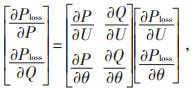
|
(9) |
则有:
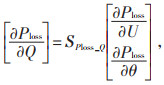
|
(10) |
式中:SPloss_Q为式(9)中Jacobi矩阵逆的子矩阵。
计算节点i的网损对相角和电压的偏导可得:
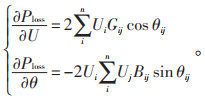
|
(11) |
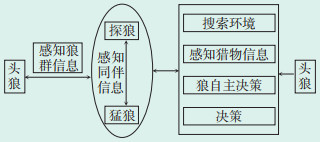
狼群算法(Wolf Pack Algorithm,WPA)是由我国学者吴虎胜等人提出的一种群体智能优化算法,其基本原理是狼群合作捕食猎物。狼群由头狼、探狼和猛狼等三种身份的个体组成,它们的职责划分如图 1所示。WPA算法原理简单,容易实现,目前被广泛应用于医疗、能源、交通等领域[9],其优化原理可参考文献[10]。
|
| 图 1 狼群个体职责划分 Figure 1 Individual responsibility division of wolf pack |
研究表明,WPA算法中的探狼游走策略中存在无效游走的现象,其猛狼运动步长采用固定步长也不利于围捕猎物,为了提升WPA算法的效果,本文提出两种策略对WPA算法进行改进。
3.1.1 改进探狼游走策略在WPA算法中,原本探狼共有4个游走方向,但实际只有两个方向,因为游走参数取2和4时,探狼位置不变,只有游走参数取1和3时,探狼的位置才会发生变化,因此,本文对探狼游走策略进行改进,具体如下:
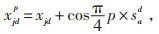
|
(12) |
式中:xjdp为游走后的探狼位置;xjd为探狼当前位置;d为空间维数;p为游走参数,p=1、2、3、4;sad为探狼游走步长。
由式(12)可知,当p取1时,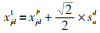
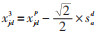
在WPA算法中,猛狼向猎物运动的步长和猛狼攻击猎物的步长均设置为固定值,在迭代后期,二者不断减小有利于算法进行局部搜索,避免陷入局部最优,为此,本文对猛狼运动步长进行动态设置,具体如下:

|
(13) |
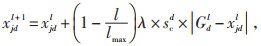
|
(14) |
式中:gdl、Gdl分别为头狼和猎物的位置;l、lmax分别为算法设置的当前迭代次数和最大迭代次数;λ为常数;scd为猎物运动步长;sbd为猛狼运动步长。
仿真分析表明,相比WPA算法,IWPA算法的全局搜索能力和局部搜索能力都得到增强,能够加快目标函数收敛,提高计算精度。
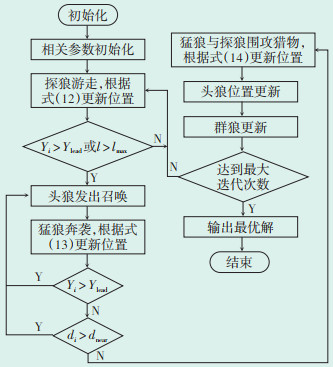
3.2 IWPA算法求解配电网无功优化模型考虑到IWPA算法良好的优化性能,本文采用IWPA算法对含风电配电网无功优化模型进行求解,图 2为IWPA算法的优化流程图,具体步骤如下:
|
| 图 2 IWPA算法优化流程 Figure 2 IWPA algorithm optimization process 图中:Ylead—头狼适应度值;Yi—探狼适应度值;dnear—头狼与猎物之间的距离;di—最小距离。 |
(1)设置配电网运行参数及IWPA算法的相关参数,主要包括人工狼数量,探狼最大的游走次数、步长因子、比例因子、距离判定因子和最大迭代次数等,具体参数设置参考文献[11]。
(2)根据目标函数式(1)计算头狼适应度值;
(3)根据式(12)对探狼位置进行更新,直到探狼适应度优于头狼,用该探狼替换头狼,进行下一步,否则,继续游走直至达到最大迭代次数后进行下一步;
(4)根据式(13)对猛狼位置进行更新,直到探狼适应度优于头狼,用该猛狼替换头狼,否则继续奔袭直到与头狼距离小于最小攻击距离时进行下一步;
(5)根据式(14)对猎物进行围攻,并更新头狼;
(6)对整个狼群的位置进行更新;
(7)判断算法是否达到最大迭代次数,若是则输出寻优结果,否则返回步骤(3)。
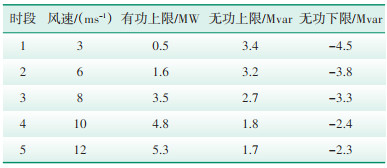
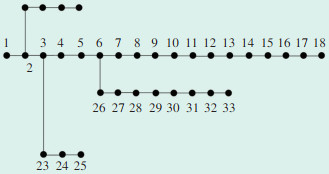
4 算例分析采用IEEE33节点配电系统建立仿真模型,其网络拓扑图如图 3所示,系统各节点参数可参考文献[12]。系统基准电压和基准功率分别为12.66 kV和10 MVA,系统负荷为3715+j2300 kVA。将4台总容量为6 MW的风电机组接入末端节点18,每台风电机组的容量均为1.5 MW,其机端额定电压为690 V,表 1给出了不同时段风速及风电机组输出功率的上下限,每台SVG无功补偿装置的最大输出功率均为100 kvar。
|
| 图 3 IEEE33节点配电系统 Figure 3 IEEE33 node distribution system |
| 表 1 不同时段风速及风电机组输出功率的上下限 Table 1 Upper and lower limits of wind speed and output power of wind turbines at different time periods |
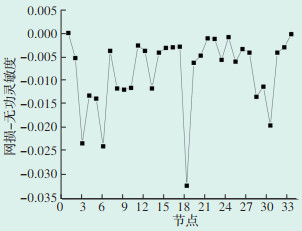
利用灵敏度分析法原理进行编程,对各节点网损-无功灵敏度进行计算,结果如图 4所示。由图 4可知,灵敏度较大的4个节点依次是3、6、18和30,因此选择上述4个节点安装SVG,对配电网系统进行无功补偿。
|
| 图 4 灵敏度计算结果 Figure 4 Sensitivity calculation results |
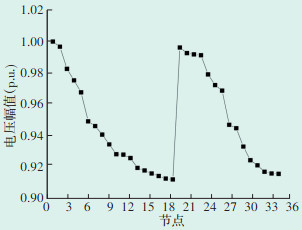
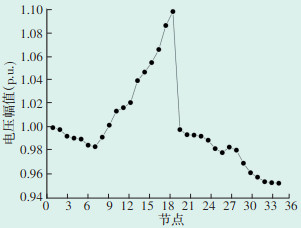
在风电机组接入配电网前和接入配电网后,配电网有功网络损耗分别为200.68 kW和406.75 kW,各节点电压幅值分别如图 5和图 6所示。对比图 5和图 6可知,配电网中接入风电后,部分节点电压幅值提升明显,有些节点电压幅值超过了1.05(p.u.),在风机接入位置的电压幅值提升最大,由此可以看出,配电网中风电接入会影响电压质量,另外,在风电接入后,配电网网络损耗由200.68 kW增加至406.75 kW,网损增长102.68%,说明风电接入后线路损耗也在增加。因此,对于风电接入的配电网需要进行无功补偿。
|
| 图 5 风电接入前各节点电压幅值 Figure 5 Voltage amplitude of each node before wind power integration |
|
| 图 6 风电接入后各节点电压幅值 Figure 6 Voltage amplitude of each node after wind power integration |
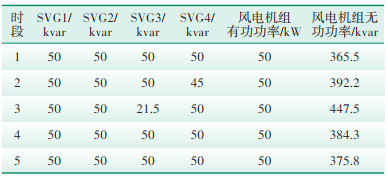
为了比较不同风速下风电并网的无功优化效果,本文以0.5 h为一个时段对含风电配电网系统进行无功补偿,选取其中5个时段,优化结果见表 2。
| 表 2 含风电配电系统无功优化结果 Table 2 Reactive power optimization results of the power distribution system including wind power |
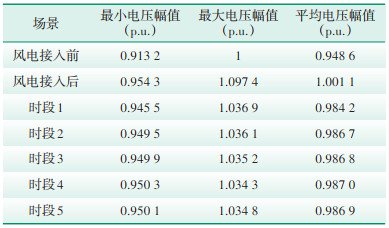
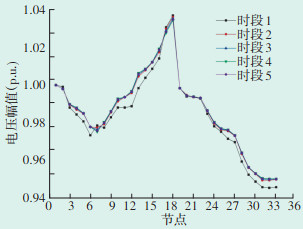
无功优化后各时段节点电压幅值变化曲线如图 7所示,风电接入前后及各时段电压幅值对比情况如表 4所示。结合图 7和表 3可以看出,风速变化对无功优化的效果影响较小,经无功优化后的配电网节点电压波动范围明显减小,各时段节点电压幅值均在0.94~1.04(p.u.),相比风电接入前后的平均电压幅值更接近1。由此可见,对含风电配电网进行无功优化能够降低电压波动,提高电压质量。
|
| 图 7 无功优化后各时段节点电压幅值 Figure 7 Node voltage amplitude at different time periods after reactive power optimization |
| 表 3 风电接入前后及各时段电压幅值对比 Table 3 Comparison of voltage amplitudes before and after wind power integration and at different time periods |
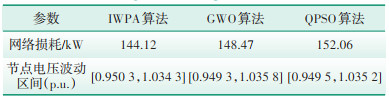
| 表 4 三种算法对时段4优化结果对比 Table 4 Comparison of optimization results of three algorithms for period 4 |
各时段无功优化后配电网网络损耗如图 8所示,从图 8可以看出,各时段网损相比风电接入后的网损明显降低,且低于风电接入前的网损,可见对含风电配电网进行无功优化能够进一步降低网络损耗,验证了本文提出的含风电配电网无功优化方法的正确性。

|
| 图 8 各时段无功优化后配电网网络损耗 Figure 8 Distribution network loss after reactive power optimization at different time periods |
为了进一步验证IWPA算法的优越性,采用文献[13]中的灰狼优化算法(Grey Wolf Optimization,GWO)和文献[14]中的量子粒子群算法(Quantum Particle Swarm Optimization,QPSO)对本文算例进行无功优化,其他条件保持不变,表 4给出了IWPA算法、GWO算法和QPSO算法对时段4进行无功优化的网络损耗和节点电压波动情况,对比表 4中数据可知,采用IWPA算法进行优化时的网络损耗为144.12 kW,节点电压波动区间为[0.950 3,1.034 3],网损损耗和节点电压波动范围均小于其他两种方法,验证了改进IWPA算法在含风电配电网无功优化方面的优越性。
5 结束语以配电网节点电压总偏移指数最小作为目标函数,综合考虑各类约束,建立了基于改进狼群算法的含风电配电网无功优化模型,通过改进探狼游走策略和动态设置猛狼运动步长,以增强IWPA算法的优化性能,并利用灵敏度分析确定无功补偿位置,采用IEEE33节点配电系统进行算例分析,结果表明,采用IWPA算法进行优化时的网络损耗为144.12 kW,节点电压波动区间为[0.950 3,1.034 3],优于其他配电网无功优化方法,验证了本文所提无功优化方法的正确性和优越性。
| [1] |
宋剑波. 风力发电技术的现状与发展综述[J].
集成电路应用, 2022, 39(4): 148-149 SONG Jianbo. Overview of the Current Situation and Development of Wind Power Generation Technology[J]. Applications of IC, 2022, 39(4): 148-149 (  0) 0)
|
| [2] |
王旭, 闫世杰, 张新宇, 等. 基于半不变量法概率潮流的光伏配电网风险评估[J].
东北电力技术, 2022, 43(10)1-5, 11 WANG Xu, YAN Shijie, ZHANG Xinyu, et al. Risk Assessment of Photovoltaic Distribution Network Based on Probabilistic Power Flow With Cumulant Method[J]. Northeast Electric Power Technology, 2022, 43(10)1-5, 11 (  0) 0)
|
| [3] |
崔庆雪, 李霞林, 葛磊蛟, 等. 计及时滞的含风电配电网节点电压安全分析[J].
电工技术学报, 2023, 38(5): 1299-1311 CUI Qingxue, LI Xialin, GE Leijiao, et al. Safety analysis of node voltage in wind power distribution networks considering time delay[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1299-1311 DOI:10.19595/j.cnki.1000-6753.tces.212097 (  0) 0)
|
| [4] |
陈康, 王泽, 郭永吉. 基于grcForest模型的风电并网系统暂态电压稳定评估[J].
智慧电力, 2023, 51(1): 31-37 CHEN Kang, WANG Ze, GUO Yongji. Transient voltage stability assessment of wind power grid connected systems based on the grcForest model[J]. Smart Power, 2023, 51(1): 31-37 (  0) 0)
|
| [5] |
向东, 陈松, 季益俊, 等. 智能化含风电配电网多目标协同调度模型[J].
电网与清洁能源, 2022, 38(7)127-133, 140 XIANG Dong, CHEN Song, JI Yijun, et al. An Intelligent Multi-Objective Collaborative Dispatching Model for Distribution Networks Containing Wind Power[J]. Advances of Power System & Hydroelectric Engineering, 2022, 38(7)127-133, 140 (  0) 0)
|
| [6] |
杨旭, 王瑞, 余畅文, 等. 基于改进灰狼优化算法的分布式能源系统优化调度[J].
内蒙古电力技术, 2023, 41(1): 26-33 YANG Xu, WANG Rui, YU Changwen, et al. Distributed energy system optimization scheduling based on improved grey wolf optimization algorithm[J]. Inner Mongolia Electric Power, 2023, 41(1): 26-33 (  0) 0)
|
| [7] |
汪林光, 谢小荣, 贺静波, 等. 采用多元线性回归方法分析短路比对风电并网系统小干扰稳定性的影响[J].
电力建设, 2023, 44(4): 113-118 WANG Linguang, XIE Xiaorong, HE Jingbo, et al. Using multiple linear regression method to analyze the impact of short circuit ratio on small interference stability of wind power grid connected systems[J]. Electric Power Construction, 2023, 44(4): 113-118 (  0) 0)
|
| [8] |
肖建华, 李春亮, 黄晓权, 等. 基于粒子群算法的含风电配电网无功优化研究[J].
电工技术, 2022(18)133-134, 139 XIAO Jianhua, LI Chunliang, HUANG Xiaoquan, et al. Research on Reactive Power Optimization of Distribution Network with Wind Power Based on Particle Swarm Optimization[J]. Electric Engineering, 2022(18)133-134, 139 (  0) 0)
|
| [9] |
甘子莘, 荆朝霞. 考虑风电接入和负荷转供的配电网可靠性成本[J].
广东电力, 2021, 34(8): 22-28 GAN Zishen, JING Chaoxia. Reliability Cost of Distribution Networks Considering Wind Power Access and Load Transfer[J]. Guangdong Electric Power, 2021, 34(8): 22-28 (  0) 0)
|
| [10] |
吕齐, 李明轩, 魏韡, 等. 基于参数规划的含储能和风电电力系统低碳经济调度[J/OL]. 电力自动化设备: 1-10[2023-04-25]. https://doi.org/10.16081/j.epae.202204044.
LYU Qi, LI Mingxuan, WEI Wei, et al. Low carbon economic dispatch of power systems including energy storage and wind power based on parameter planning[J/OL]. Electric Power Automation Equipment: 1-10[2023-04-25]. https://doi.org/10.16081/j.epae.202204044. (  0) 0)
|
| [11] |
杜晓东, 陈泽, 赵百捷, 等. 基于双传播模型的含风电场的配电网谐波谐振影响分析[J].
电网与清洁能源, 2022, 38(4): 129-134 DU Xiaodong, CHEN Ze, ZHAO Baijie, et al. Analysis of harmonic resonance effects in distribution networks containing wind farms based on a dual propagation model[J]. Advances of Power System & Hydroelectric Engineering, 2022, 38(4): 129-134 (  0) 0)
|
| [12] |
李彦晨, 贾燕冰, 谢栋. 计及电能质量影响的配电网风储优化配置[J/OL]. 电网技术: 1-13[2023-04-25]. http://kns.cnki.net/kcms/detail/11.2410.TM.20220414.1602.004.html.
LI Yanchen, JIA Yanbing, XIE Dong. Optimal allocation of wind storage in distribution networks considering the impact of power quality[J/OL]. Power System Technology: 1-13[2023-04-25]. http://kns.cnki.net/kcms/detail/11.2410.TM.20220414.1602.004.html. (  0) 0)
|
| [13] |
鲁裕婷, 赵天乐, 都洪基, 等. 基于改进粒子群算法的含DG配电网无功优化[J].
电力工程技术, 2018, 37(6): 69-74 LU Yuting, ZHAO Tianle, DU Hongji, et al. Reactive Power Optimization of Distribution Networks with DG Based on Improved Particle Swarm Optimization[J]. Jiangsu Electrical Engineering, 2018, 37(6): 69-74 (  0) 0)
|
| [14] |
苏福清, 匡洪海, 钟浩. 基于AG-MOPSO的含风电配电网无功优化[J/OL]. 电源学报: 1-12[2023-04-25]. http://kns.cnki.net/kcms/detail/12.1420.tm.20220106.1221.002.html.
SU Fuqing, KUANG Honghai, ZHONG Hao. Reactive Power Optimization of Wind Power Distribution Network Based on AG-MOPSO[J/OL]. Journal of Power Supply: 1-12[2023-04-25]. http://kns.cnki.net/kcms/detail/12.1420.tm.20220106.1221.002.html. (  0) 0)
|
| [15] |
王凯悦. 基于蚁狮算法的含风电的配电网无功优化分析与研究[D]. 西安: 西安石油大学, 2021.
(  0) 0)
|
| [16] |
全少理, 郭勇, 杨卓, 等. 基于灵敏度分析的交直流配电网无功补偿策略[J].
电力科学与技术学报, 2021, 36(5): 104-112 QUAN Shaoli, GUO Yong, YANG Zhuo, et al. Reactive Power Compensation Strategy for AC and DC Distribution Networks Based on Sensitivity Analysis[J]. Journal of Electric Power Science and Technology, 2021, 36(5): 104-112 (  0) 0)
|
| [17] |
吴虎胜, 张凤鸣, 吴庐山. 一种新的群体智能算法——狼群算法[J].
系统工程与电子技术, 2013, 35(11): 2430-2438 WU Husheng, ZHANG Fengming, WU Lushan. A new swarm intelligence algorithm-wolf swarm algorithm[J]. Systems Engineering and Electronics, 2013, 35(11): 2430-2438 (  0) 0)
|
| [18] |
汪晗, 李启迪, 黄治翰, 等. 基于WPA优化LSSVM的输电线路覆冰厚度预测[J].
东北电力技术, 2022, 43(2): 42-46 WANG Han, LI Qidi, HUANG Zhihan, et al. Prediction of transmission line icing thickness based on WPA optimized LSSVM[J]. Northeast Electric Power Technology, 2022, 43(2): 42-46 (  0) 0)
|
| [19] |
付华, 孟繁东. 基于VMD双狼群算法的电网单相接地故障选线优化[J].
计算机应用与软件, 2019, 36(2): 269-273 FU Hua, MENG Fandong. Optimization of single - phase grounding fault line selection in power grid based on VMD double wolf swarm algorithm[J]. Computer Application and Software, 2019, 36(2): 269-273 (  0) 0)
|
| [20] |
Khanh B Q, Hojo M. Optimally selecting the location of a multiple of D-statcoms for the improvement of SARFIX due to faults in the IEEE 33 ‐ bus distribution system[J].
IEEJ Transactions on Electrical and Electronic Engineering, 2019, 14(8): 1172-1180 (  0) 0)
|
| [21] |
徐艳春, 蒋伟俊, 孙思涵, 等. 含高渗透率风电的配电网暂态电压量化评估方法[J].
中国电力, 2022, 55(7): 152-162 XU Yanchun, JIANG Weijun, Sun Sihan, et al. Quantitative evaluation method for transient voltage in distribution networks containing high permeability wind power[J]. Electric Power, 2022, 55(7): 152-162 (  0) 0)
|
| [22] |
张军, 陆文彬, 施玲君. 考虑风电布置的主动配电网电源规划[J].
东北电力技术, 2020, 41(3)5-9, 52 ZHANG Jun, LU Wenbin, SHI Lingjun. Active Distribution Network Power Planning Considering Wind Farms Layout[J]. Northeast Electric Power Technology, 2020, 41(3)5-9, 52 (  0) 0)
|
| [23] |
白洁, 王守相, 赵倩宇, 等. 考虑风电出力不确定性的配电网概率潮流计算[J].
电力系统及其自动化学报, 2021, 33(1): 78-84 BAI Jie, WANG Shouxiang, ZHAO Qianyu, et al. Probabilistic power flow calculation of distribution networks considering uncertainty of wind power output[J]. Proceedings of the CSU-EPSA, 2021, 33(1): 78-84 (  0) 0)
|
| [24] |
倪爽, 崔承刚, 郑庆荣, 等. 基于多风电相关性场景生成法的配电网随机多目标无功优化[J].
浙江电力, 2020, 39(11): 103-111 NI Shuang, CUI Chenggang, ZHENG Qingrong, et al. Stochastic Multi - objective Reactive Power Optimization of Distribution Network Based on Multiple Wind Turbines Correlative Scenario Generation Method[J]. Zhejiang Electric Power, 2020, 39(11): 103-111 (  0) 0)
|
 2023, Vol. 41
2023, Vol. 41