随着并网发电技术的不断发展,使得风光等新能源具备了大规模开发的条件,建设集中式新能源电站是高效利用新能源的主要方式[1-2]。但是,由于新能源的间接性和强随机波动性,直接大规模并网将会对电力系统的调度运行产生较大影响[3-4]。新能源电站配置一定容量的储能或购买储能,通过储能调峰能力来平抑新能源功率波动,成为目前减少弃风弃光现象和提升并网发电能力的有效手段[5-6]。
针对新能源电站和储能系统的研究主要包括:利用储能的能量时移特性对负荷进行跟踪,消除新能源反调峰特性影响[7-10];利用储能的快速响应特性抵消新能源预测值和实际值的差额,提升新能源预测精度,研究针对新能源预测不平衡和优化储能配置[11-14];利用储能平滑新能源出力波动,保持电力系统安全稳定运行,研究针对新能源波动平滑的控制策略[15-16]。
目前,在储能系统平抑新能源电站出力波动方面,国内外学者均开展了相关研究工作,提出了一些较为实用的平抑算法,比较主流的算法包括滤波算法、模型预测算法。文献[17]利用一阶低通滤波器将新能源输出功率的中高频波动分量剔除,达到平滑并网功率的效果。但电网侧与电力电子变换器均存在谐波,同时低通滤波算法对新能源功率波动较为敏感,使得该控制策略适应性不强,且滤波时间参数难以确定。而在设备级的功率调节方面,文献[18]是基于直流有源滤波器实现直流链纹波电流的抑制。文献[19]利用荷电状态(State of Charge,SOC)偏差、频率偏差以及滤波时间常数之间的关系确定滤波时间常数,使得储能系统的SOC工作在正常范围内。因计算量小、原理简单,低通滤波算法在平滑新能源波动中得到广泛应用。部分学者采用了模型预测控制的技术以平滑新能源功率波动。文献[20]结合风电场功率预测技术,充分考虑储能电池放电深度、SOC等因素,有效实现平滑输出功率,但该策略需要有超高的风功率预测水准。文献[21]将两个一阶滤波分配算法串联构成二阶滤波算法,根据超级电容荷电状态自适应调节其滤波时间常数,使超级电容荷电值处于缓冲区时,基于变时间常数分配高低频功率,对混合储能各部分进行平抑。文献[22]构建了低通滤波器与模型预测控制之间的联系,实现了新能源功率波动平抑。上述技术方案均可对新能源输出功率进行分解,得到高频的波动功率和较平滑的并网功率,但在协调有效平滑新能源功率波动和电网谐波统一控制的问题上,效果并不理想,可能造成并网功率的过度平滑,加大储能系统的负担。基于此,构建一种同时兼顾平滑新能源电站功率波动和电网谐波治理的控制策略具有重要的应用价值和研究意义。
针对上述问题,本文提出一种能平抑新能源电站功率波动和谐波治理的储能系统控制策略。首先,给出了储能系统平滑可再生能源电站波动控制结构,实现有功无功的解耦控制。其次,基于低通滤波原理构建平滑控制策略,获得不同天气情况下滤波时间常数的选取原则。最后,提出了储能系统平抑新能源电站功率波动和有源滤波的统一控制策略,通过储能系统的控制策略实现了平抑新能源功率波动与电网谐波治理。
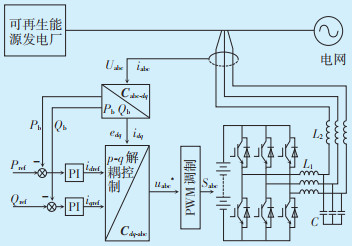
1 储能系统平抑功率波动解耦控制模型储能变流器(Power Conversion System,PCS)可实现储能电池与交流电网之间双向能量传递,一般由DC/AC逆变器和LCL滤波器组成。变流器的并网控制策略为PQ控制,即通过控制并网电流实现变流器吸收或释放给定的有功和无功功率。储能系统平抑新能源电站功率波动的控制结构如图 1所示。
|
| 图 1 储能平抑新能源电站功率波动控制示意图 Figure 1 Schematic diagram of power fluctuation control for energy storage suppression of new energy power station 图中:Uabc为并网点电压;iabc为并网点电流;Cabc-dq为转换到dq坐标系的变换矩阵;edq为dq坐标系下的电压;idq为dq坐标系下的电流;Pref为有功参考功率;Qref为无功参考功率;Pb为储能系统实际发出有功功率;Qb为储能系统实际发出无功功率;idref为Pref与Pb经PI控制器输出的有功电流指令;iqref为Qref与Qb经PI控制器输出的无功电流指令;Cdq-abc为解耦到三相坐标系的变换矩阵;uabc*为经过波动控制后的电压;Sabc为新能源电站平抑控制后功率;L1和L2为滤波电感;C为滤波电容。 |
PCS采用传统的PI控制,但在正弦量控制中,PI控制难以达到无差跟踪目标。因此,通过dq坐标变换,将三相交流电流转换到旋转坐标系下进行控制。LCL滤波器是在dq坐标系下的高阶耦合系统,当电容值远小于电感时,LCL滤波器可以忽略电容的耦合作用,直接采用电感滤波控制方式。而电容值较大时,需要在dq坐标系下进行解耦控制。为了实现解耦控制,在dq坐标系中将三相并网电流转换成两相坐标系下的直流量,从而使PI控制起到有效的误差调节作用。dq坐标系中,解耦变换矩阵Tabc/dq可表示为:
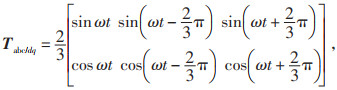
|
(1) |
式中:ω为网侧电压角频率(由锁相环检测网侧电压相位得到),rad/s;t为时间,s。
在模型中引入电容电流ICabc可得:
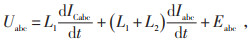
|
(2) |
式中:Uabc、ICabc、Iabc和Eabc分别表示变流器输出电压,V,滤波电容电流,A,网侧电流,A,网侧电压,V。
对公式(2)进行dq坐标变换,结果见式(3)—(4):
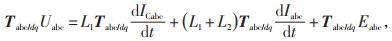
|
(3) |
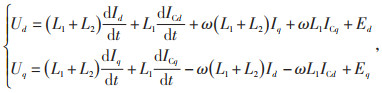
|
(4) |
式中:Ud与Uq、Id与Iq、ICd与ICq、Ed与Eq分别表示变流器d、q轴输出电压、网侧电流、滤波电容电流和网侧电压的坐标分量。
在公式(4)中,微分项的数值可通过PI控制器计算得到,其余项可通过交叉解耦方式进行补偿,即可实现PQ的解耦控制。其中,ω由锁相环PLL检测网侧电压获得,在理想情况下令Eq=0,而Ed为相电压幅值。
综上所述,有功参考功率Pref由平滑可再生能源功率波动控制策略决定,无功参考功率Qref由电网调度指令提供;储能系统实际发出有功Pb和无功功率Qb,由测量电压Uabc和电流iabc计算所得。Pref与Pb经PI控制器输出有功电流指令idref,Qref与Qb经PI控制器输出无功电流指令iqref。PCS基于上述得到idref与iqref,通过PQ解耦控制实现储能释放吸收有功功率和无功功率,达到平抑电站出力波动和满足电力系统对无功的需求。
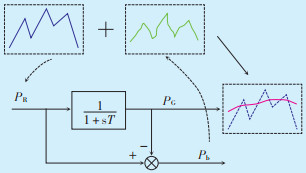
2 基于低通滤波原理的平滑控制策略为保持新能源电站处于最大发电能力,通常仅输出有功功率PR,无功功率QR为0。将电站输出的PR经过低通滤波器处理后,可滤除高频成分,得到注入电力系统的平滑功率PG。图 2为一阶低通滤波原理,其中T表示滤波时间常数,该参数对储能功率容量确定及新能源波动平抑效果具有重要作用。
|
| 图 2 低通滤波算法简图 Figure 2 Schematic diagram of low-pass filtering algorithm |
在不考虑储能运行损耗的情况下,PG可由公式(5)计算得到。储能系统充放电功率Pb由公式(6)计算得到,经由能量管理系统确定有功给定值指令Pref。为分析简便,储能系统提供无功功率Qref为0。
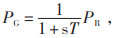
|
(5) |
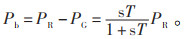
|
(6) |
低通滤波器波特图特性如图 3所示。其幅频函数为单调递减函数,当频率ω取0时,幅值达到最大值1;当频率为ωc时(即截止频率),幅值为0.707。由此可知,大于截止频率的波动将被抑制。由于频率和滤波时间常数T成反比,因此当T取值较大时,经一阶低通滤波后输入电网的功率波动则越小。
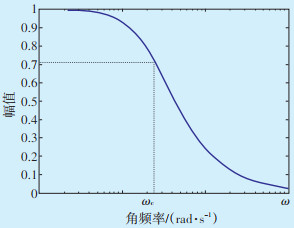
|
| 图 3 一阶低通滤波器波特图 Figure 3 Baud diagram of first-order low-pass filter |
图 4给出了不同时间常数下储能出力传递函数的波特图。从图中可以看出,对于滤波时间常数为T1的曲线,理论上储能可以补偿频率大于ω1的所有波动,且有ω1 < ω2 < ω3,而滤波时间常数T1>T2>T3,也就是说,滤波时间常数越大,储能所补偿的频率范围就越大。
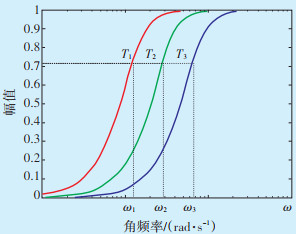
|
| 图 4 不同时间常数下储能传递函数波特图 Figure 4 Baud diagram of energy storage transfer function under different time constants |
由于天气的多变性,可再生能源电站实际功率波动通常小于最大功率波动值,因此参与平滑可再生能源功率波动的储能系统往往有较高剩余容量,导致设备利用率低。为此基于有源滤波器电路拓扑和控制结构,提出了具有平滑功率波动与有源滤波功能统一的控制模式,其控制结构如图 5所示,主要包括谐波电流检测、储能能量管理系统、平滑控制、功率限幅模块、电流指令合成与PWM信号调制等功能环节。
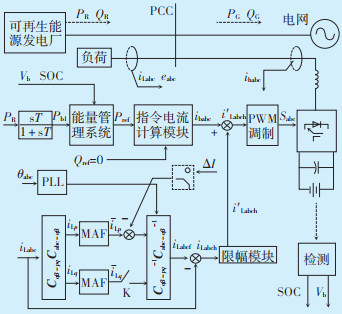
|
| 图 5 储能系统平滑波动与有源滤波功能统一控制结构 Figure 5 Unified control structure for smooth fluctuation and active filter functions of energy storage system 图中:PCC为新能源电站并网点;Vb为蓄电池系统在使用或充电状态下电化学反应所提供的电动势;eabc为测量电压;PLL为锁相环;Pb1为储能系统实际发出有功功率;ΔI为反馈电流差;MAF为滑动平均滤波;iLabc为有源滤波电流,ibabc为平滑波动电流;iLabch为谐波电流实测值;i′Labch为限幅后谐波电流值;ihabc为额定电流;iLp为基波有功电流;iLp为基波无功电流;iLp为滤波后的有功电流;iLp为滤波后的无功电流;iLabcf为三相静止坐标系的电流;K为无功电流滤波开关;Caβ-pq为α、β两相坐标系向pq坐标系的变换矩阵,Cabc-aβ为三相坐标系向α、β坐标系的变换矩阵。 |
将电站的输出信号PR经过低通滤波器处理后,可滤除高频成分,得到注入电力系统的平滑信号PG。储能系统提供无功功率Qref由电网调度指令决定,为分析简便,令储能系统提供无功功率Qref为0。为了便于对谐波电流进行限幅处理,选择在三相坐标系下合成储能系统平滑波动与有源滤波的电流指令。因此,根据瞬时功率理论,将Pref、Qref转换到三相静止坐标系下pref、qref,电流指令iba、ibb、ibc由公式(7)—(10)推导计算得到。
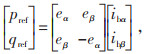
|
(7) |
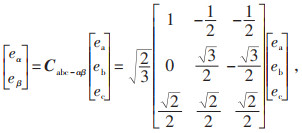
|
(8) |
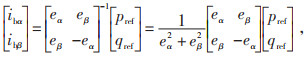
|
(9) |
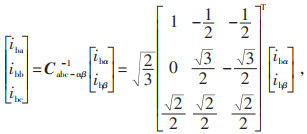
|
(10) |
式中:eα、eβ为在两相绕组下的电压值,V;ea、eb、ec为测量电压,V;ibα、ibβ为两相静止坐标系下的电流指令。
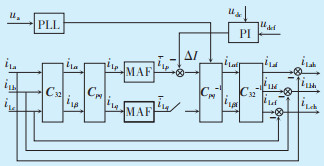
3.2 谐波电流指令检测基于瞬时功率理论的谐波检测电路是有源滤波功能实现的关键,检测电路如图 6所示。
|
| 图 6 谐波电流检测电路 Figure 6 Harmonic current detection circuit 图中:C32为三相静止坐标系到两相静止坐标系的转换矩阵;Cpq为pq变换的转换矩阵;iLa、iLb、iLc为有源滤波电流;iLα、iLβ为变换后相互正交的电流信号;iLah、iLbh、iLch为谐波电流;iLaf、iLbf、iLcf为三相静止坐标系的电流;ua为储能系统实际的电压值;udc为实际电压值;udcf为参考电压值;iLαf、iLβf为分离谐波后的电流信号。 |
基于瞬时功率理论的谐波检测电路,可以由式(11)求得谐波电流iLabch。
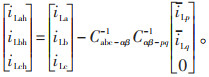
|
(11) |
当不考虑储能PCS的容量限制,储能系统在实现平滑波动功能时,可以完全补偿电网谐波电流,此时储能系统限幅钳位电流i*Lah、i*Lbh、i*Lch可由公式(12)计算得到:
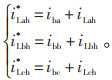
|
(12) |
然而,实际中储能的PCS剩余功率容量是不确定的。当注入电网的谐波电流动态变化时,储能系统补偿谐波电流所需的功率容量可能存在不足。为此,需要合理协调控制系统中有源滤波电流iLabch和平滑波动电流ibabc,以确保储能PCS运行在安全范围内。
储能系统主要处理新能源电站输出功率波动,当PCS有剩余功率容量时,则对注入电网的谐波电流进行补偿。为确保PCS的运行安全以及利用剩余容量进行谐波处理,本文采用幅值钳位逻辑算法得到补偿谐波电流的指令。该逻辑限幅电路的功能结构如图 7所示。以L1相电路为例,当iLah max≤ΔIS,不需要电流限幅即可实现对所有谐波电流的补偿;当iLah max>ΔIS,则需要对电流进行限幅处理,既保证PCS工作在安全范围,又能充分利用开关电流的裕量。
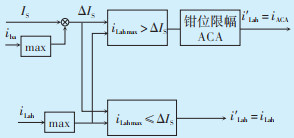
|
| 图 7 钳位限幅控制结构 Figure 7 Clamp limiting control structure 图中:IS为开关管额定电流;iba为储能系统平滑功率波动的电流;i′Lah为限幅后的谐波电流;iLah max为幅值;ΔIS为开关电流裕量;iACA为钳位电流。 |
公式(13)为限幅电路模型:

|
(13) |
针对电力系统负荷大多为非线性,采用电流幅值钳位算法(Amplitude Clamping Algorithm,ACA),见公式(14)。将参考电流指令钳位在给定值,截断超出部分。
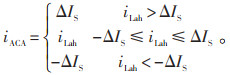
|
(14) |
基于Simulink平台搭建光伏储能仿真模型,其中光伏出力峰值30 kW,储能系统额定容量83 kWh,额定充放电功率均为25 kW。PCS内含控制模块、LCL滤波电路和逆变桥,具体参数见文献[11]。
4.1 储能系统解耦控制效果分析为验证储能变流器PQ解耦控制策略,在0.1 s、0.2 s与0.3 s分别改变有功功率和无功功率的给定值。图 8为储能系统同时控制有功和无功出力仿真结果,由于实现了有功无功解耦控制,有功充放电与无功吸收释放互不影响。
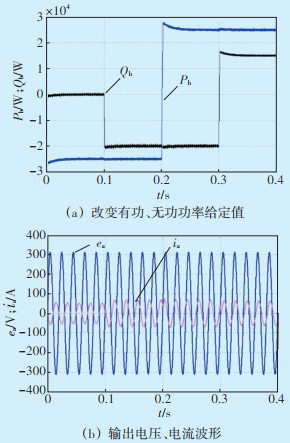
|
| 图 8 有功无功独立控制 Figure 8 Independent control of active and reactive power |
图 9为光伏发电系统短时功率曲线和给定光伏发电功率曲线。图 10为按照给定光伏发电功率曲线,储能所需提供的有功功率和储能网侧输出电压电流波形。
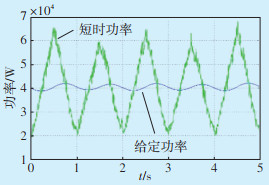
|
| 图 9 光伏短时功率波形和给定光伏发电功率曲线 Figure 9 Short term photovoltaic output power waveform and given photovoltaic power generation curve |
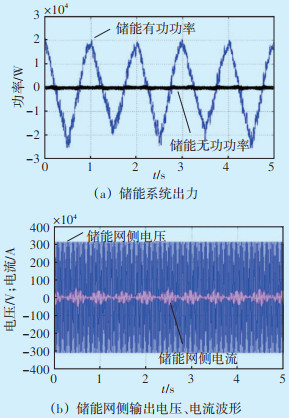
|
| 图 10 储能系统出力和电压、电流波形 Figure 10 Output and voltage and current waveform of energy storage system |
图 11为未加入储能系统时光伏单元输出电压电流波形。由于光伏功率的波动,导致注入电网电流幅值大小发生变化。图 12为加入储能系统后,光储系统注入电网的电压电流波形。由于储能的调控功能,注入电网的电流幅值基本恒定。
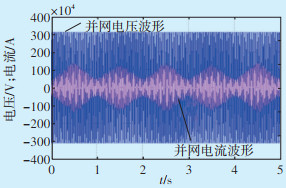
|
| 图 11 未接储能时并网处电压、电流波形 Figure 11 Voltage and current waveform at grid-connected point when no energy storage is connected |
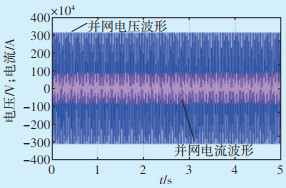
|
| 图 12 接储能时并网处电压、电流波形 Figure 12 Voltage and current waveform at grid-connected point when energy storage is connected |
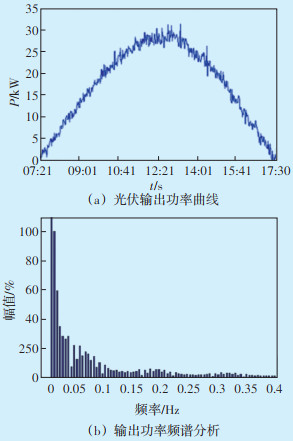
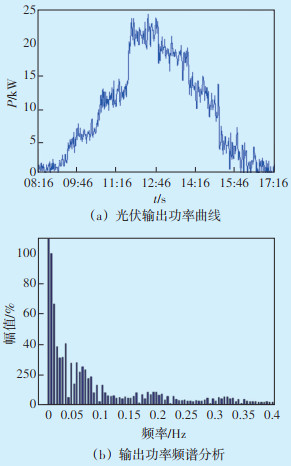
以光伏输出功率曲线为例,对晴天、多云两种典型天气情况的光伏曲线进行频谱分析,结果分别如图 13、图 14所示。
|
| 图 13 晴天天气光伏输出功率曲线和频谱分析(波动集中在0.2 Hz以下) Figure 13 Photovoltaic output power curve and spectrum analysis on sunny days (Fluctuations concentrated below 0.2 Hz) |
|
| 图 14 多云天气光伏输出功率曲线和频谱分析(波动集中在0.25 Hz以下) Figure 14 Photovoltaic output power curve and spectrum analysis on cloudy days (Fluctuations concentrated below 0.25 Hz) |
通过对光伏数据进行频谱分析,得出以下结论,光伏出力的波动比较缓慢,大多集中在0.25 Hz以下,高频率的波动所占比例很小,可忽略不计。因此,设置一阶低通滤波器的时间常数时应保持储能系统补偿频率在0.25 Hz附近波动,可实现平滑光伏出力曲线,且滤波时间常数T越大,可补偿的频段越大。
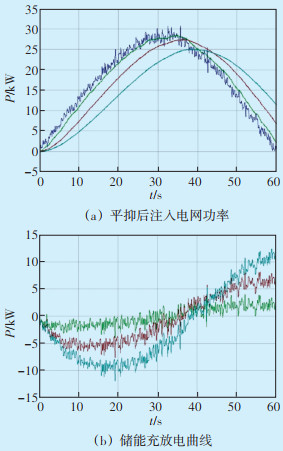
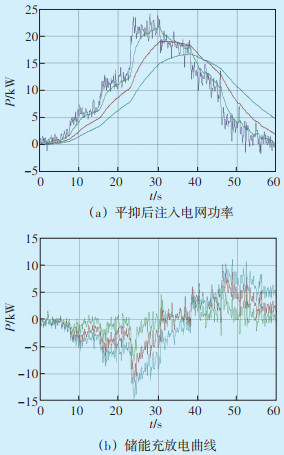
针对不同的天气情况,进行不同时间常数的仿真,得到平抑后注入电网功率与储能充放电曲线,分别如图 15、图 16所示。
|
| 图 15 晴天天气仿真情况 Figure 15 Simulation on sunny days |
|
| 图 16 多云天气仿真情况 Figure 16 Simulation on cloudy days |
通过对两种天气进行仿真可得出以下结论:低通滤波器的时间常数选取越大,输入电网的功率越平滑,对储能提出的要求就越高,需要储能的功率与容量也越大。考虑到一天中光伏的波动程度随着天气情况变化而变化,结合上文对不同天气情况的频谱分析,可根据不同天气情况选择滤波时间常数,如晴天光伏波动较小,选择较小的时间常数;多云天气,其波动较大,波动频率范围也大,可选择较大的时间常数。
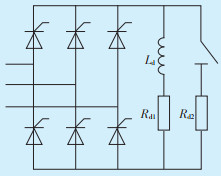
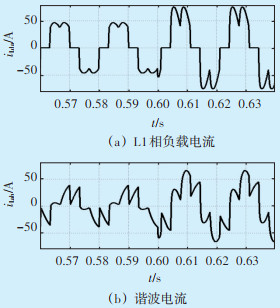
4.3 平滑功率波动与有源滤波功能的验证分析图 17为三相整流负载的谐波源。设置参数为:三相电源L1相中ea=311sinωt,Ld=10 mH,Rd1=10 Ω,Rd2=10 Ω。在仿真中通过改变触发延迟角α和负载突增来模拟负载的随机特性。当t处于0~0.6 s时,为Rd1Ld串联型负载,且α=30°;当t处于0.6~1.2 s时,为Rd1Ld并联Rd2负载,在0.6 s时开关闭合,且α=50°。图 18给出了开关闭合时附近的L1相负载电流及谐波电流波形。当t=0.6 s时负载突增,导致负载基波电流和谐波含量增大。
|
| 图 17 三相整流负载谐波源 Figure 17 Three-phase rectifier load harmonic source |
|
| 图 18 相负载电流与谐波电流 Figure 18 Phase load current and harmonic current |
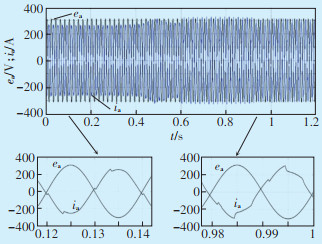
仿真1:图 19展示了当储能系统只进行平抑新能源波动时的L1相网侧电压ea和电流ia波形及两处波形的局部放大图。可以看出注入电网的电流ia幅值保持恒定,说明储能系统平抑新能源波动的效果良好。当t处在0.45~0.55 s时,电网电流ia稍微波动,因为电池储能系统平滑波动所需功率超过了其额定功率,能量管理系统对电池单元输出功率进行限幅控制,平滑功能不能完全实现。由于储能系统没有滤波功能,导致电网电流含有谐波。当负载谐波电流增大时,会加剧电网电流ia的畸变,降低功率因数。
|
| 图 19 平滑波动时电网电压与电流 Figure 19 Grid voltage and current in smooth fluctuation |
仿真2:当储能系统具备平抑功率波动和滤波功能时,图 20展示了L1相网侧电压ea和电流ia波形及三处波形的局部放大图。在平抑波动的控制下,使得注入电网电流ia幅值保持恒定。在放大图中,电流ia与电压ea相位差180°,且近似为正弦波,说明储能系统对滤除注入电网电流谐波的效果良好。当t处于0.9~1.1 s时,可以看到电网电流有微小畸变。导致该现象的原因为:当前时段储能谐波补偿及平抑波动所需电流指令幅值较大,开关器电流裕量小于谐波电流幅值。为保证储能系统运行在安全范围内,对统一控制的电流指令采用幅值钳位ACA电路进行限幅处理。
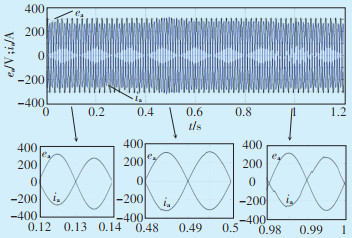
|
| 图 20 统一控制时电网电压与电流 Figure 20 Grid voltage and current under unified control |
对仿真1注入电网电流ia进行频谱分析,如图 21(a)所示,得到总谐波畸变率(Total Harmonics Distortion,THD)结果如下:当t处在0~0.6 s时,THD为4.80%;当t处在0.6~1.2 s时,THD为8.22%。对仿真2注入电网电流ia进行频谱分析,如图 21(b)所示。当t处在0~0.6 s时,THD为0.18%;当t处在0.6~1.2 s时,THD为1.51%。由上述结果可知,储能系统具备有源滤波功能,可有效抑制注入电网电流谐波,从而提升了电能质量。图 22为仿真1和2条件下,储能系统平滑可再生能源电站输出功率波动仿真结果,两者平滑效果基本相同。

|
| 图 21 电网电流频谱分析 Figure 21 Spectrum analysis of power grid current |
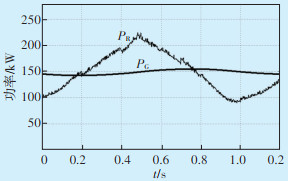
|
| 图 22 注入电网功率 Figure 22 Power injected into the grid |
针对储能系统平滑新能源电站功率波动存在平抑性能与电网谐波治理难以协调的问题,本文提出了一种基于低通滤波原理的储能系统平滑新能源电站波动的控制策略,得到结论如下:
(1)低通滤波器的时间常数选取越大,注入电网的功率越平滑,所需储能系统的功率容量与能量容量也越大;
(2)在满足平滑功率波动的前提下,采用幅值钳位逻辑算法对补偿谐波电流指令进行限制,可确保储能PCS运行安全,并且能高效利用剩余功率容量对入网电流谐波进行抑制;
(3)具备有源滤波功能的储能系统可有效消除电流谐波,改善电能质量。
| [1] |
熊鸿韬, 汪宗恒, 尚磊, 等. 一种用于电力系统低频振荡抑制的新能源电站阻尼注入控制器设计及特性分析[J].
电网技术, 2022, 46(7): 2690-2700 XIONG Hongtao, WANG Zongheng, SHANG Lei, et al. Damping Injection Controller of Renewable Energy for Power System Low Frequency Oscillation Mitigation and Its Dynamic Characteristics Analysis[J]. Power System Technology, 2022, 46(7): 2690-2700 (  0) 0)
|
| [2] |
王卫, 王海云, 张再驰, 等. 自同步型新能源并网振荡机理及电压致稳控制[J].
电力电子技术, 2023, 57(2): 77-80 WANG Wei, WANG Haiyun, ZHANG Zaichi, et al. Oscillation Mechanism and Voltage Stabilization Control of Self-synchronous New Energy Grid-connected[J]. Power Electronics, 2023, 57(2): 77-80 (  0) 0)
|
| [3] |
刘映尚, 马骞, 王子强, 等. 新型电力系统电力电量平衡调度问题的思考[J/OL]. 中国电机工程学报: 1-12[2022-12-22].
(  0) 0)
|
| [4] |
孔祥玉, 张烜墉, 王成山, 等. 复杂形态下的配电网自适应自趋优状态估计方法[J].
中国电机工程学报, 2021, 41(10): 3339-3348 KONG Xiangyu, ZHANG Xuanyong, WANG Chengshan, et al. Adaptive Self-optimizing State Estimation Method of Distribution Network in Complex Condition[J]. Proceedings of the CSEE, 2021, 41(10): 3339-3348 (  0) 0)
|
| [5] |
谢毓广, 李金中, 王川, 等. 考虑消纳水平的新能源配套储能和输电通道容量协调优化配置[J/OL]. 电力自动化设备: 1-10[2022-12-22].
(  0) 0)
|
| [6] |
刘烨, 程杉, 王瑞, 等. 基于小波降噪和深度学习的电能质量扰动分类方法[J].
电力系统及其自动化学报, 2022, 34(11): 17-23 LIU Ye, CHENG Shan, WANG Rui, et al. Power Quality Disturbance Classification Method Based on Wavelet Denoising and Deep Learning[J]. Proceedings of the CSU-EPSA, 2022, 34(11): 17-23 (  0) 0)
|
| [7] |
崔杨, 安宁, 付小标, 等. 考虑广义储能与碳捕集设备联合调峰的电力系统低碳经济调度[J/OL]. 电力自动化设备: 1-18[2022-12-22].
(  0) 0)
|
| [8] |
李军徽, 张嘉辉, 穆钢, 等. 储能辅助火电机组深度调峰的分层优化调度[J].
电网技术, 2019, 43(11): 3961-3970 LI Junhui, ZHANG Jiahui, MU Gang, et al. Hierarchical Optimization Scheduling of Deep Peak Shaving for Energy-storage Auxiliary Thermal Power Generating Units[J]. Power System Technology, 2019, 43(11): 3961-3970 (  0) 0)
|
| [9] |
Li M, Li Y, Choi S S. Dispatch Planning of a Wide-Area Wind Power-Energy Storage Scheme Based on Ensemble Empirical Mode Decomposition Technique[J].
IEEE Transactions on Sustainable Energy, 2021, 12(2): 1275-1288 DOI:10.1109/TSTE.2020.3042385 (  0) 0)
|
| [10] |
禹海峰, 黄婧杰, 蒋诗谣, 等. 计及储能使用年寿命的风电场整体性储能配置[J].
电力科学与技术学报, 2022, 37(4): 152-160 YU Haifeng, HUANG Jingjie, JIANG Shiyao, et al. The overall energy storage configuration of wind farms considering the service life of electric energy storage[J]. Journal of Electric Power Science and Technology, 2022, 37(4): 152-160 (  0) 0)
|
| [11] |
孔祥玉, 郑锋, 鄂志君, 等. 基于深度信念网络的短期负荷预测方法[J].
电力系统自动化, 2018, 42(5): 133-139 KONG Xiangyu, ZHENG Feng, E Zhijun, et al. Short-term Load Forecasting Based on Deep Belief Network[J]. Automation of Electric Power Systems, 2018, 42(5): 133-139 (  0) 0)
|
| [12] |
谢丽蓉, 郑浩, 魏成伟, 等. 兼顾补偿预测误差和平抑波动的光伏混合储能协调控制策略[J].
电力系统自动化, 2021, 45(3): 130-138 XIE Lirong, ZHENG Hao, WEI Chengwei, et al. Coordinated Control Strategy of Photovoltaic Hybrid Energy Storage Considering Prediction Error Compensation and Fluctuation Suppression[J]. Automation of Electric Power Systems, 2021, 45(3): 130-138 (  0) 0)
|
| [13] |
Khosravi M, Afsharnia S, Farhangi S. Optimal sizing and technology selection of hybrid energy storage system with novel dispatching power for wind power integration[J].
International Journal of Electrical Power & Energy Systems, 2021, 127(1): 106660 DOI:10.1016/j.ijepes.2020.106660 (  0) 0)
|
| [14] |
Huang W, Zhang X, Li K, et al. Resilience oriented planning of urban multi-energy systems with generalized energy storage sources[J].
IEEE Transactions on Power Systems, 2021, 37(4): 2906-2918 DOI:10.1109/TPWRS.2021.3123074 (  0) 0)
|
| [15] |
刘军, 甘乾煜, 张泽秋, 等. 考虑储能电池运行寿命的风电功率波动平抑方法研究[J/OL]. 电网技术: 1-11[2022-12-22].
(  0) 0)
|
| [16] |
马兰, 谢丽蓉, 叶林, 等. 基于混合储能双层规划模型的风电波动平抑策略[J].
电网技术, 2022, 46(3): 1016-1029 MA Lan, XIE Lirong, YE Lin, et al. Wind Power Fluctuation Suppression Strategy Based on Hybrid Energy Storage Bi-level Programming Model[J]. Power System Technology, 2022, 46(3): 1016-1029 (  0) 0)
|
| [17] |
张晴, 李欣然, 杨明, 等. 净效益最大的平抑风电功率波动的混合储能容量配置方法[J].
电工技术学报, 2016, 31(14): 40-48 ZHANG Qing, LI Xinran, YANG Ming, et al. Capacity Determination of Hybrid Energy Storage System for Smoothing Wind Power Fluctuations with Maximum Net Benefit[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 40-48 (  0) 0)
|
| [18] |
丁明, 陈中, 程旭东. 级联储能变换器直流链纹波电流的抑制策略[J].
电工技术学报, 2014, 29(2): 46-54 DING Ming, CHEN Zhong, CHENG Xudong. A Scheme for Suppressing DC Ripple Current of Cascade Converter for Energy Storage System[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 46-54 (  0) 0)
|
| [19] |
贾焦心, 颜湘武, 李铁成, 等. 基于改进RoCoF测量方法的储能辅助光伏机组快速调频策略[J].
电工技术学报, 2022, 37(S1): 93-105 JIA Jiaoxin, YAN Xiangwu, LI Tiecheng, et al. Fast Frequency Regulation Strategy of PV Power System Assisted by Energy Storage Based on Improved Measurement Method of RoCoF[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 93-105 (  0) 0)
|
| [20] |
李滨, 邓有雄, 陈碧云. 含超短期风功率预测增强处理的风储系统超前滚动优化控制策略[J].
电网技术, 2021, 45(6): 2280-2287 LI Bin, DENG Youxiong, CHEN Biyun. Advanced Rolling Optimization Control Strategy for Wind Storage System With Enhanced Ultra-short-term Wind Power Prediction[J]. Power System Technology, 2021, 45(6): 2280-2287 (  0) 0)
|
| [21] |
李烁, 陆洲杰, 吴光源, 等. 基于混合储能的光伏微电网研究[J].
东北电力技术, 2022, 43(7): 1-4 LI Shuo, LU Zhoujie, WU Guangyuan, et al. Research on Photovoltaic Microgrid Based on Hybrid Energy Storage[J]. Northeast Electric Power Technology, 2022, 43(7): 1-4 (  0) 0)
|
| [22] |
Ma Q, Wang H, Luo P, et al. Real-time control strategy of tractive load peak clipping and valley filling based on model predictive control[J].
IEEE Transactions on Transportation Electrification, 2022, 8(3): 3208-3218 DOI:10.1109/TTE.2022.3163135 (  0) 0)
|
 2023, Vol. 41
2023, Vol. 41


