2. 国网福建省电力有限公司厦门供电公司, 福建 厦门 361004
2. State Grid Fujian Electric Power Co., Ltd, Xiamen Power Supply Company, Xiamen 361004, China
作为传输电能的重要节点,变电站的稳定运行对整个输电网络的安全稳定运行至关重要。变电站电气设备接地部分与接地网通过接地引下线进行连接,在设备长期运行过程中,接地引下线可能会因潮湿和酸碱度较大等因素而出现腐蚀甚至断裂等现象,导致接地引下线与主接地网间的电阻增大,严重时会造成设备失地运行。为了避免出现上述隐患,需要定期进行接地引下线导通测试,目的是检查各种电气设备之间各部分接地装置及设备之间电气连接情况,从而判断各设备接地部分的接地是否良好。
国家出台了与接地引下线导通测试相关的电力行业标准[1],规定了其参数测试、电器完整性测试、工频特性参数测试及土壤电阻率测试等基本要求和方法。文献[2-4]对比了几种接地导通测试方法的优缺点,分析了各种测试方法的适用场景和数据准确度;文献[5]通过设计新型接线钳缩短了变电站变电运维接地导通测试工作时长,提高了运维人员的测试效率;文献[6]分析了接地网不同部位断裂时接地网导通电阻的变化规律,并提出相应的判断接地网腐蚀缺陷的依据;文献[7]对接地导通测试的测量数据不确定度进行了理论分析,有助于对接地导通测试仪的准确性和可靠性进行评估。然而,上述文献只是针对接地导通的测试方法和接地网的导通数据进行了分析,忽视了变电站现场实际接地导通测试的过程。目前还未有文献对现场接地导通测试的过程优化策略进行研究。
实际上,无论采用何种接地导通测试方法,测试流程基本不变,主要包括参考点与测试点的选择和移动,接地导通测试仪的启动和使用,直流电阻或交流阻抗值的记录等。传统的测量流程存在如各场区难以找到合适的参考点,测试线过长导致的测量误差增大,测试人员移动距离长、劳动强度大等问题,降低了接地导通测试的精度和效率。为了解决以上问题,本文提出一种新型的接地导通测试流程优化策略,摒弃了传统测量流程中固定参考点、改变测试点的测量方式,参考点与测试点交替改变。这种新型策略避免了基准参考点的选择,将测量范围限制在各场区局部小区域内,解决了测试线过长导致测量误差增大和测试人员移动距离过长的问题,并结合矩阵逆运算获得更高的数据精度,有效提升接地导通测试的效率和数据准确度。
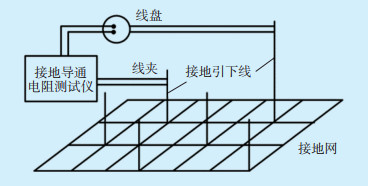
1 传统接地导通测试流程及存在的问题 1.1 测试流程以直流电压电流法[8]为例,传统接地导通测试接线如图 1所示,测试主要步骤如下:
|
| 图 1 接地导通测试接线 |
(1)选取参考点和测试点。先找出与接地网连接良好的接地引下线作为参考点,考虑到变电所场地太大,测试线不宜过长,将变电所划分为多个场区,分别在各场区选择参考点进行测量。
(2)连接电压和电流回路,将接地导通电阻测试仪输出分别连接到参考点、测试点。
(3)启动接地导通电阻测试仪,使仪器输出固定直流电流值,记录相应的直流电阻值。
(4)使直流电流输出降至零,断开电源,将测试点移至下一位置,依次测试并记录。
1.2 存在的问题可以看出,整个测试过程存在以下问题:
(1)参考点的选择对测量结果有明显影响。与接地网接地良好的接地引下线难以通过定量的方法进行选择,一般按照经验选择多点接地的设备作为参考点,而其实际的接地电阻无法测量,若选择的参考点接地电阻过大,将导致其他测试点测量结果误差过大甚至不合格,需更换参考点重新测量。
(2)测量范围过大。将变电站划分为多个场区进行测量,在每个场区测试时进行更换参考点,所有设备无法基于同一参考点进行测量,而不同参考点接地电阻不同导致各场区的测量误差有差别。
(3)测试范围过大、测试线过长均会导致测量误差增大;测试人员移动距离过长,降低了测试的效率。
2 新型接地导通测试流程优化策略不同于传统测试流程中固定参考点、改变测试点的方法,新型测试流程采用参考点和测试点交替改变的方法进行测量,测试主要步骤如下:
(1)在场区或接地网边缘选取两个相邻设备的接地引下线分别作为参考点和测试点。
(2)连接电压和电流回路,将接地导通电阻测试仪输出分别连接到参考点、测试点。
(3)启动接地导通电阻测试仪,使仪器输出固定直流电流值,记录相应的直流电阻值。
(4)使直流电流输出降至零,断开电源,将测试点移至下一相邻位置设备接地引下线,将参考点移至上一测试点,交替进行测试。
(5)最后将第一次测试时的参考点作为测试点进行最终测量,使整个测试形成闭环。
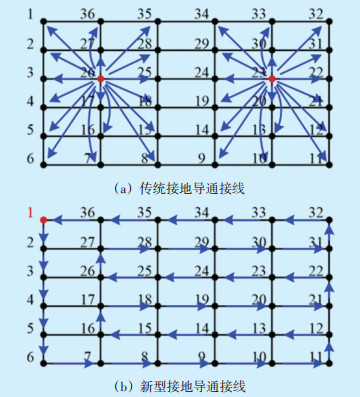
以一个6×6的矩阵型接地网为例,图 2给出两种测试流程策略中参考点和测试点的选择示意图。由图 2可见,在传统接地导通测试中测试区域被分为两部分,26号和23号节点作为接地导通良好的参考点,对其他测试点依次进行测量,得到接地电阻。在新型接地导通测试中,起始参考点不固定,这里选为1号节点,2号节点选为测试点,测试完毕后将2号节点作为新的参考点,3号节点选为测试点,进行下一次测试,以此类推,最后将36号节点作为参考点,1号节点作为测试点进行测试,使整个测试闭环。
|
| 图 2 参考点和测试点的选择 |
以上分析可以看出,新型接地导通测试流程不需要预先对参考点进行选择,也无需将变电站划分为多个场区,测试范围大幅缩小,大大缩短了测试线的长度和测试人员的移动距离,提高了整个测试流程的效率。
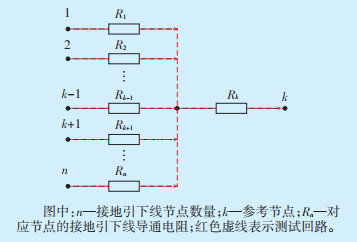
3 测量原理和误差比较 3.1 测量原理对比对于传统接地导通测试,在选定固定参考点后,测试点测量得到的直流电阻值即为当前设备接地引下线的接地导通电阻,考虑到接地引下线的腐蚀率要远高于主接地网[1],可以认为主接地网各节点之间为导通良好的导体,因此传统接地导通测试原理可以简化为图 3。
|
| 图 3 传统接地导通测试原理 |
由图 3可见,在给定参考节点k,经过n-1次测量后,可以得到所有接地引下线的导通电阻,如式(1)所示:

|
(1) |
式中:Rcn表示第n个接地引下线的导通电阻测量值,当测试选择的固定参考点接地导通良好时,可认为Rk趋近于0,则有Rc1=R1,Rc2=R2,…,Rck=0,…,Rcn=Rn,即理想状态下,传统接地导通测试的测量值为接地引下线导通电阻的真实值。实际上,受多参考点选择和设备情况的影响,Rk不可能为零,导致测量结果存在一定偏差。
对于新型接地导通测试,在选定初始参考点和测试点后,测量得到的直流电阻值并非当前测试点接地引下线导通电阻,而为参考点和测量点的接地引下线导通电阻之和,如式(2)所示:
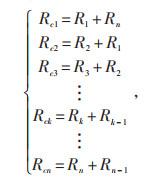
|
(2) |
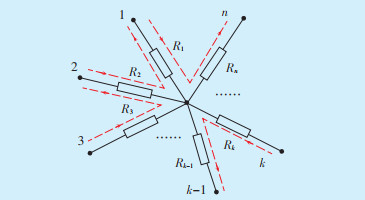
其导通测试原理图如图 4所示。
|
| 图 4 新型接地导通测试原理 |
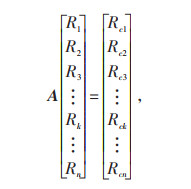
由图 4可见,新型接地导通测试中第n个测试点的导通电阻测量值为当前测试点和参考点的接地引下线导通电阻之和。为了得到各测试点接地引下线的导通电阻,需要对式(2)进行求解。为方便求解,将其写成矩阵形式,如式(3)所示:
|
(3) |
其中,A为系数矩阵,表达式为:

|
(4) |
对[R1,R2,R3,…,Rn]T进行求解,首先需要对系数矩阵A求逆。通过计算A的行列式可以判断A的逆矩阵是否存在,结果如式(5)所示。
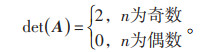
|
(5) |
由式(5)可见,n为奇数时,矩阵A行列式值为2,其逆矩阵存在;n为偶数时,矩阵A行列式值为0,其逆矩阵不存在。换言之,当接地引下线节点数量为奇数时,式(3)所示方程组为适定方程组,存在唯一解,可以通过求解A的逆矩阵得到各接地引下线接地导通电阻的真实值;当接地引下线节点数量为偶数时,式(3)所示方程组为欠定方程组,存在无穷多组解,无法确定各接地引下线导通电阻的真实值。因此,对于一个总接地节点数为偶数的接地网,需要将其拆分为节点数各为奇数的两部分,分别进行闭环测量。例如,图 2所示的36节点接地网便可拆分成17节点和19节点的两个接地网,分别对其进行闭环测量。在接地网节点为奇数或将接地网划分为奇数节点的各部分后,便可以通过求解A的逆矩阵得到各接地引下线的导通电阻。以n为奇数为例,如式(6)所示:
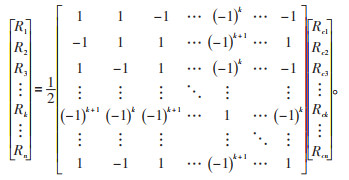
|
(6) |
由式(6)即可计算各接地引下线的接地导通电阻值。
3.2 测量误差对比在测量过程中,由于测量方法本身的缺陷和测量仪器的分辨率较低或测试人员读数视差会导致接地导通电阻的测量值与实际值之间出现误差,这种误差称为测量误差。在传统接地导通测试中,测量误差包含系统误差和随机误差两部分,系统误差即为参考点接地引下线导通电阻,引入随机误差Δri后,接地导通电阻的测量值修正为:
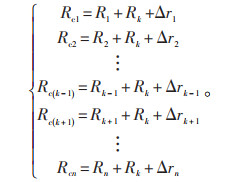
|
(7) |
为了衡量测量误差对传统接地导通测试结果造成的误差,引入均方误差的计算公式:

|
(8) |
结合均值不等式,可以对M1的极小值进行估算,结果如式(9)所示:

|
(9) |
由式(9)可见,传统接地导通测量结果最小均方误差估算值由三部分组成:一是参考点接地引下线导通电阻Rk的平方项,二是各测试点随机误差平均值,三是各测试点随机误差平均值的平方项。其中参考点接地引下线导通电阻Rk的数量级要高于随机误差,对测量误差的影响最大;其次为随机误差平均值;影响最小的为各测试点随机误差平均值的平方项。
对于新型接地导通测试,测量误差仅包含随机误差,随机误差经矩阵运算后传播至最终计算结果。引入随机误差Δri后,接地导通电阻测量值修正为:

|
(10) |
同样的,可以计算其均方误差:

|
(11) |
同样的,结合均值不等式可以对M2的极小值进行估算:
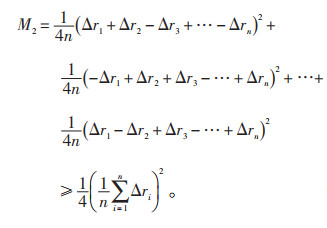
|
(12) |
由式(12)可见,新型接地导通测试的测量误差经过矩阵逆运算之后的最小均方误差估算值,仅包含各测试点随机误差平均值的平方项,并且当Rk= 0,即测试误差仅包含随机误差时,新型接地导通测试结果的误差也仅为传统测量的1/4。由此可见,新型接地导通测试的接地引下线导通电阻的计算方法大大降低了测量结果的误差,提高了数据精度。
4 仿真案例分析以图 2所示36节点矩阵接地网为例,分别对采用不同接地导通测试方法所得接地引下线接地导通电阻进行计算,比较二者测量结果的误差。
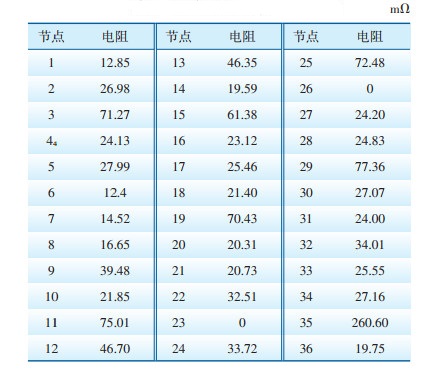
首先,对图 2所示36节点矩阵接地网的各节点接地引下线导通电阻进行假设,如表 1所示。
| 表 1 各节点接地引下线导通电阻 |
根据文献[1]中对于设备接地状况的判断标准,导通电阻在50 mΩ以下的设备接地状况良好;50 ~ 200 mΩ的设备接地状况尚可,需要重点关注;200 mΩ~1 Ω的设备接地状况不佳,重要设备应尽快检查处理。按照上述标准,表 1中接地状况良好的节点集合为{1,2,4,5,6,7,8,9,10,12,13,14,16,17,18,20,21,22,23,24,26,27,28,30,31,32,33,34,36},接地状况尚可的节点集合为{3,11,15,19,25,29},接地状况不佳的节点集合为{35}。
对于传统接地导通测试,按照传统接地导通测量流程,首先选择导通良好的23和26节点作为固定参考点,分别对两个接地网场区进行测量。场区一以节点26作为基准参考点,对{1,2,3,4,5,6,7,8,15,16,17,18,25,27,28,35,36}的节点集合进行测量;场区二以节点23作为基准参考点,对{9,10,11,12,13,14,19,20,21,22,24,29,30,31,32,33,34}的节点集合进行测量。为了反映测量过程中产生的随机误差,假设随机误差满足最常见的高斯分布,其概率密度函数如式(13)所示:

|
(13) |
式中:σ为尺度参数,μ为位置参数。令σ=0.5 mΩ,μ= 0,结合反函数法可以生成两个17维的随机误差向量,分别表示为:

|
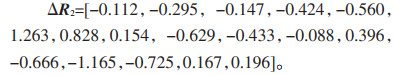
|
综合以上数据,结合式(7)给出的传统接地导通测试计算公式,可对传统接地导通测试方法的接地导通电阻测量值进行计算,结果见表 2。
| 表 2 传统接地导通测试测量值 |
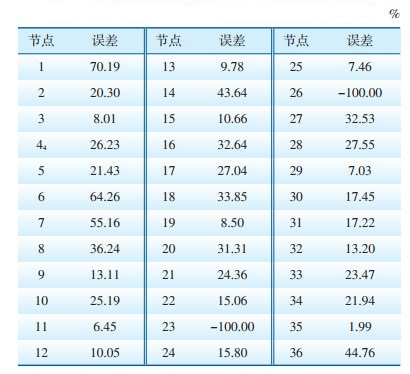
为了直观对比测量值与真实值间的误差,对每个测试节点的相对误差进行计算,结果如表 3所示。由表 3可以看出,不同测试节点的测量值和真实值间相对误差差距很大,接地导通电阻越小的节点相对误差越大,这是由于所有测试节点测量值计算均引入了参考节点接地导通电阻的固定系统误差,接地导通电阻小的测试节点系统误差的占比越大,导致相对误差越大。相较于固定的系统误差,随机误差对测量结果产生的影响较小,负值随机误差还略微降低了测量的相对误差。需要注意的是,参考节点23,26的相对误差为-100%,原因是测试中认为参考节点为理想接地点,接地导通电阻为0。式(14)计算了测量结果的均方误差,其值约等于两参考点接地导通电阻均值的平方,由结果可以看出,传统接地导通测量结果的误差主要是由参考点的接地导通电阻决定。
| 表 3 传统接地导通测试测量值与真实值相对误差 |

|
(14) |
对于新型接地导通测试,首先将36节点的矩阵接地网划分为两个接地网场区。场区一为{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17}的节点集合,包含17个节点;场区二为{18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36}的节点集合,包含19个节点。同样的,测试中的随机误差向量满足μ=0,σ=0.5 mΩ的高斯分布,结合反函数法生成的17维和19维随机误差向量可表示为:
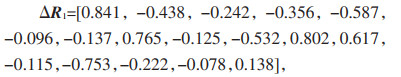
|

|
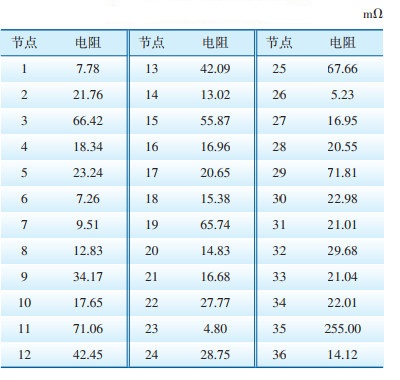
结合式(6)与式(10),可对新型接地导通测试方法的接地导通电阻测量值进行计算,其结果如表 4所示。同样的,各测试节点的计算值和真实值间相对误差如表 5所示。
| 表 4 新型接地导通测试计算值 |
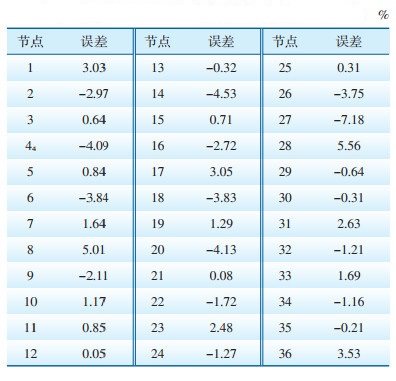
| 表 5 新型接地导通测试测量值与真实值相对误差 |
由表 5可见,相比较于传统接地导通测试,新型接地导通各测试节点计算值的相对误差大大降低,绝大部分测试节点的相对误差均控制在5%以内,少部分测试节点由于某些过大的随机误差经矩阵逆运算传递给计算值而造成相对误差偏大,但仍小于10%,计算结果仍优于传统接地导通测试的测量值。此外,新型接地导通测试克服了传统接地导通测试中接地导通电阻越小测量值相对误差越大的问题,其计算值相对误差不受接地导通电阻值影响,近似服从均值为零的高斯分布。同样的,式(15)计算了测量结果的均方误差,其值约等于服从高斯分布的随机误差尺度参数σ的平方,由结果可以看出,新型接地导通测量结果的误差由测量误差的随机分布情况决定。由此可见,新型接地导通测试大大提升了接地导通电阻值的测量精度,同时避免了传统接地导通测试的相对误差分布不均的问题。

|
(15) |
新型接地导通测试流程优化策略采用了参考点与测试点交替改变的方式,结合测量数据和矩阵逆运算对各测试节点接地引下线的导通电阻进行计算,避免了基准参考点的选择,减小了测量范围,解决了测试线过长导致测量误差增大和测试人员移动距离过长的问题。通过对比分析传统和新型接地导通测试的测试原理和测量误差及对二者接地导通电阻测量和计算值与真实值间均方误差的计算,表明新型接地导通测试优化策略避免了传统接地导通测试的系统误差,减小了测量随机误差,大大提高了数据精度。
目前,大多变电站现场依然使用传统接地导通测试方法,本文提出的新型接地导通测试优化策略在减轻了测试人员劳动强度的同时提高了测量精度,对变电站具有一定的工程应用价值,对保障变电站的安全稳定运行起到了积极的作用。
| [1] |
中国电力企业联合会. 接地装置特性参数测量导则: DL/T 475-2006[S]. 北京: 中国电力出版社, 2008.
(  0) 0)
|
| [2] |
程连彦, 戴向伟, 耿颖杰, 等. 变电站多点接地设备导通测试分析[J].
电子技术, 2020, 49(4): 118-119 (  0) 0)
|
| [3] |
董刚. 接地导通测试仪测量不确定度评估[J].
工业计量, 2017, 27(5): 47-48 (  0) 0)
|
| [4] |
曹小龙. 电力设备接地引下线导通测试方法的探讨[J].
电瓷避雷器, 2010(5): 41-44, 47 (  0) 0)
|
| [5] |
郑厚昌, 韦明小, 任达香, 等. 缩短变电站变电运维接地导通测试工作时间[J].
电力技术, 2021(6): 136-137 (  0) 0)
|
| [6] |
郭美玉, 朱小明, 陆新东, 等. 双回路接地导通电阻测试仪测量方法研究[J].
工业计量, 2019, 29(6): 83-85, 89 (  0) 0)
|
| [7] |
梁庆凡, 孙标, 刘卫新. 接地导通电阻测试仪测量结果的不确定度评定[J].
轻工标准与质量, 2019, 164(增刊2): 90-91 (  0) 0)
|
| [8] |
张仁豫, 陈昌鱼, 王昌长.
高电压试验技术[M]. 2版. 北京: 清华大学出版社, 2008.
(  0) 0)
|