2. 内蒙古自治区新型电力系统智能电网企业重点实验室,呼和浩特 010020;
3. 重庆交通大学土木工程学院,重庆 400074
2. Inner Mongolia Enterprise Key Laboratory of New Power System Smart Grid, Hohhot 010020, China;
3. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China
随着我国西电东送工程的实施,高压、特高压输电线路里程增长,杆塔、导线和金具数量增加,输电线路维护的难度越来越大。近年极端天气频发,进一步增加了发生线路故障的可能性,金具损坏事故时有发生[1-6],2023年1月内蒙古电网某高压输电线路发生大风作用下金具断裂问题,对电网的安全运行造成严重影响。对此,针对大风荷载作用下线路金具的受力分析具有重要意义[7-9]。研究该问题涉及的内容较多,例如风荷载的确定、线路结构以及金具受力仿真等。对于风荷载的计算,输电线路设计规范中主要采取等效的稳定风,该方法比较简单,而实际风速会随时间和空间发生变化,实测风速更为准确,但是受场地、成本等因素影响较难测量。为了解决这一问题,数值仿真随机风被广泛应用于输电线路相关问题分析[10-11]。获得风速值后需要对输电线路和金具进行动力学仿真,然而金具分别与杆塔和导线相连,金具之间有相互约束,针对整体结构进行有限元仿真极为困难。目前的金具有限元仿真成果均对模型进行了简化,仅对出现故障的金具建立有限元模型[12],这类简化模型不能考虑金具之间的相互运动。由于计算复杂,对整个耐张串或者绝缘子串进行有限元研究的较少[13-14]。
本文建立了输电线路整体耐张串的精细化有限元模型,通过数值模拟的随机风计算了考虑脉动效应的风荷载作用下导线动张力及其最大值,分析金具在危险荷载作用下的应力分布情况,以及大风作用下金具的力学特性,找出容易发生损坏的金具,为输电线路运维提供理论指导。
1 随机风模拟及风荷载计算 1.1 风的组成受地形和地貌的影响,靠近地面的风尤其不稳定,这种由于地面山体或建筑物阻碍气流运动,使风速和风向发生变化甚至产生漩涡的现象叫做湍流,由湍流引起的风速随机变化称为脉动风。选取空间某一点10 min平均风速,随机风由平均风和脉动风组成:
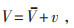
|
(1) |
式中:V为随机风速;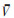
通常随机风模拟主要针对脉动风,常用的脉动风数值模拟方法有线性滤波法、谐波叠加法、逆傅里叶变换法和小波分析法等。本文采用计算精度较高的谐波叠加法模拟脉动风。对单个点进行脉动风模拟:
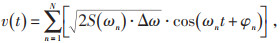
|
(2) |
式中:N为频率等分数;Δω为频率间隔值;ωn为随机风的频率,在进行具体的风速模拟时可以对该值截断,即不考虑高频和低频的脉动风,因为高频和低频的脉动风能量比较小;t为时间;φn为随机相位角,取[0,2π]内的随机数;S(ωn) 为描述脉动风能量的风速功率谱,表示不同圆频率风对应的能量。
功率谱的计算本文选取工程中常用的随高度变换的Kaimal谱:
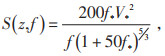
|
(3) |
式中:S(z, f) 为功率谱;V*为流场剪切速度,
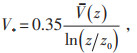
|
其中,z0为地面粗糙长度;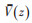
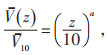
|
(4) |
其中,a为地面粗糙度系数,根据地貌情况选取;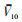
f*为无量纲的归一化频率,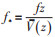
实际的输电线路跨度大,沿线不同位置的脉动风速不同,所以针对空间中脉动风的模拟需要采用谱密度矩阵来描述。设有n个脉动风速v j(t)(j = 1, 2,⋯, n) 的谱密度矩阵为:
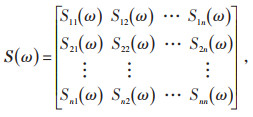
|
(5) |
式中:Sij为相距为r的空间两点的功率谱,如果i和j相同称为自功率谱Sii或者Sjj,如果i和j不同称为互功率谱Sij,其中i≠j。自功率谱可以通过公式(3)计算,互功率谱需要通过公式(6)计算:
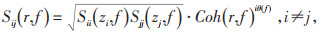
|
(6) |
式中:θ(f) 为互谱相位角;Coh(r, f) 为相干函数,根据Davenport建议采用竖向和横向相干函数:
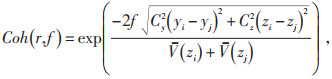
|
(7) |
式中:(yi, zi) 和(yj, zj) 分别表示空间任意两点的坐标,风速与两点的连线方向垂直;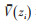
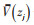
按照Cholesky分解法,可将S(ω) 分解为:
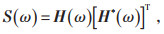
|
式中:H*(ω) 为H(ω) 的复共轭矩阵,其中,H(ω) 为下三角矩阵:
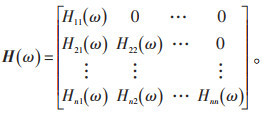
|
(8) |
可以通过谐波叠加法对空间某一点的平均风速为0的脉动风进行模拟,这种情况下脉动风速可以写为:
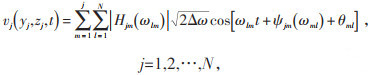
|
(9) |
式中:|Hjm(ωlm)|为下三角矩阵H(ω) 元素的模;Δω为圆频率的增量值,Δω = ωup /N,其中,ωup为高频截断频率,高于该圆频率的脉动风能量可以忽略不计,N为圆频率空间的频率划分个数;θml为在[0, 2π] 随机分布的随机相位角;ψjm(ωml) 为实部与虚部之间的夹角,可以根据公式(10)计算:
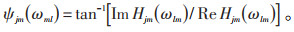
|
(10) |
为了选取合适的脉动风速周期,ωlm建议采用以下形式:
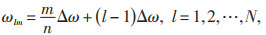
|
(11) |
式中:n为模拟的风速点数量;m为模拟的风速点;l为等分频率的累加个数。
1.3 随机风荷载计算采用谐波叠加法计算获得脉动风,与相应的平均风相加即可得到该高度随时间变换的随机风,计算得到随机风后基于准定常假设可计算风荷载,风荷载的计算见公式(12):
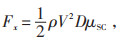
|
(12) |
式中:ρ为空气密度,kg/m3;V为高度z处的风速,m/s;μSC为输电线的体型系数,当输电线半径小于17 mm或覆冰时(不论线径大小)取1.2,导线半径大于或等于17 mm时取1.1;D为输电导线直径,mm。根据公式(12)即可计算随机风作用下导线受到的随机风荷载。
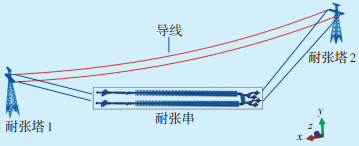
2 随机风荷载作用下导线的受力仿真分析本文选取孤立档导线为研究对象(见图 1)[15],考虑风荷载作用下杆塔对导线的影响比较小,所以忽略杆塔对导线和金具的影响,即建立有限元模型时不考虑杆塔,对导线与耐张串金具进行独立计算。建立单档的输电线路有限元模型,计算随机风荷载作用下导线的张力变化情况,得到导线的最大张力值后,将其施加到耐张串的有限元模型中,获取最大张力作用下耐张串中各金具的应力分布情况,为后期金具安全性评估及优化设计提供指导。
|
| 图 1 孤立档导线 Figure 1 Conductor of isolated span |
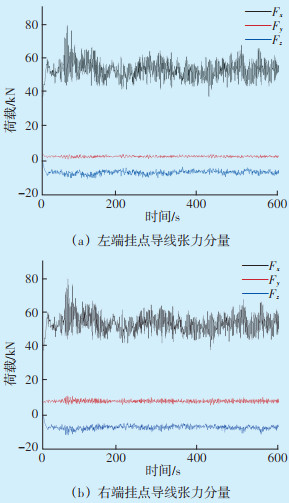
以某500 kV输电线路为例,线路特征段档距为566 m,高差为30 m,高差比为0.05,基本风速27 m/s。根据公式(9)模拟出顺线路方向的随机风速时程曲线,然后根据公式(12)计算出相应的随机风荷载,将随机风荷载施加到导线上,得到随机风荷载作用下导线张力变化情况如图 2所示。从图 2可以看出,随机风荷载作用下导线张力会产生剧烈波动,最小值接近40 kN,最大值达到80 kN,可见大风作用下随机风荷载对导线以及金具会产生较大的影响。由于有高差,所以左右两端导线的张力不一致,在接近64.4 s出现最大张力。作用于左端挂点金具的导线张力分量值为:Fx=78.7 kN,Fy=3.5 kN,Fz=-8.8 kN;作用于右端挂点金具的导线张力分量值为:Fx=78.4 kN,Fy=11.6 kN,Fz=-10.5 kN。将图 2所得的随机风荷载作用下的导线张力施加到耐张串上,即可得到最危险的张力情况下金具的应力分布情况,评估金具的安全性能。
|
| 图 2 随机风荷载作用下导线张力变化情况 Figure 2 Variation of wire tension under random wind load |
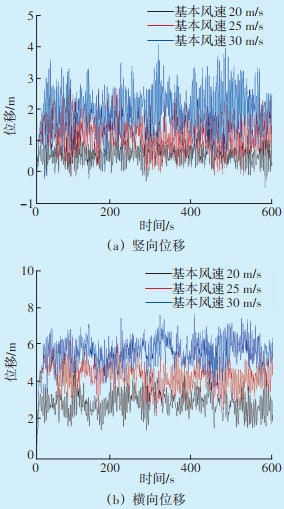
为了分析不同的基本风速对导线的振动位移和动张力的影响,分别设置了20 m/s、25 m/s、30 m/s基本设计风速,将获得的随机风输入输电线路有限元模型中,通过数值仿真方法可以得到导线中点的竖向位移、横向位移和动张力,见图 3—图 5。
|
| 图 3 不同基本风速下的跨中位移时程曲线 Figure 3 Time history curves of mid-span displacement under different basic wind speeds |
|
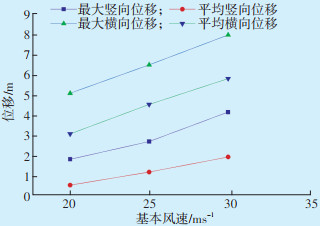
| 图 4 基本风速与最大位移、平均位移关系图 Figure 4 Diagram of the relationship between basic wind speed, maximum displacement and average displacement |
|
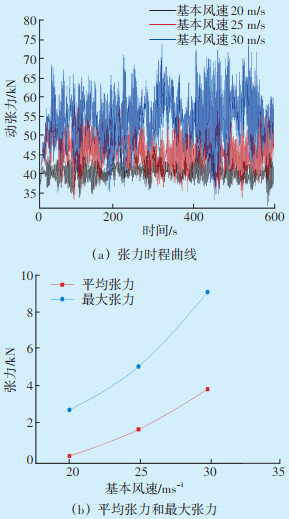
| 图 5 基本风速与挂点张力关系 Figure 5 Relationship between basic wind speed and hanging point tension |
当基本风速为20 m/s时,跨中最大竖向和横向位移分别为1.78 m和4.90 m,跨中平均竖向和横向位移分别为0.56 m和2.98 m;当基本风速为25 m/s时,跨中最大竖向和横向位移分别为2.62 m和6.24 m,跨中平均竖向和横向位移分别为1.18 m和4.37 m;当基本风速为30 m/s时,跨中最大竖向和横向位移分别为4.01 m和7.65 m,跨中平均竖向和横向位移分别为1.89 m和5.59 m。从图 4可以看出,无论选取最大值或平均值,基本风速对四分裂导线跨中位移的影响呈线性。从图 5(a)可以看出,随机风对导线的张力影响显著,随着时间增加导线的张力将产生较大的波动,基本风速对导线张力的影响大于位移;从图 5(b)可以看出,风速对张力的影响呈抛物线变化。因此,在大风地区,较大的瞬时风速会显著影响导线的动张力,需对瞬时风速进行评估,并计算其对金具的影响,防止导线及金具损坏影响输电线路安全运行。
3 耐张串金具的有限元模型 3.1 耐张串的金属部件为仿真架空输电线路金具在风荷载作用下的真实受力,以及各金具之间的相互运动情况,选取《国家电网公司输变电工程通用设计330~750 kV输电线路金具图册》中的金具图纸,建立耐张串各金具的三维实体模型,如图 6所示,包括螺栓、梯形联板等84个部件。由于耐张串中较多金具为铸件,光滑的小倒角比较多,有限元仿真非常困难,为了便于计算,在不影响结构受力分析的前提下,对模型进行了简化。如果工程中需要倒角处更为精确的局部应力,则需要单独对该金具建立更为精细的有限元模型进行仿真。
|
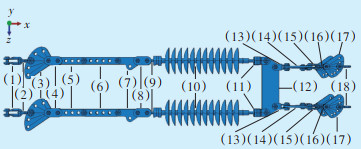
| 图 6 耐张串整体模型图 Figure 6 Overall model of strain insulator string 图中:(1)—U形挂环1;(2)—U形挂环2;(3)—DB调整板1;(4)—平行挂板1;(5)—PT调整板1;(6)—PT调整板2;(7)—牵引板;(8)—平行挂板2;(9)—球头挂环;(10)—耐张绝缘子;(11)—碗头挂板;(12)—梯形联板;(13)—直角挂板;(14)—三角挂板;(15)—上U形挂环3;(16)—下U形挂环3;(17)—DB调整板2;(18)—U形挂环4。 |
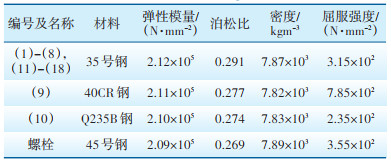
整个耐张串中金具种类比较多,对应的材料参数如表 1所示,受到试验条件的制约,钢材塑性模型选用双折线本构关系模型,屈服后的切线模量为屈服前弹性模量的百分之一。
| 表 1 耐张串各部件材料参数 Table 1 Material parameters of each part of strain insulator string |
金具网格划分对耐张串有限元分析结果的准确性及计算效率影响较大,为了提高计算效率和准确性,利用ABAQUS软件实现部件的六面体网格划分(C3D8R)。划分规则的六面体单元有助于降低模型的应力,提高计算效率。所有金具划分网格后,耐张垂串整体模型总单元数量达到225 104个,耐张串各个金具部件网格模型图 7所示。

|
| 图 7 耐张串各个金具部件网格模型 Figure 7 Mesh model of various fitting parts of strain insulator string |
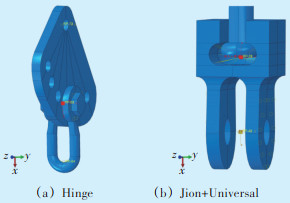
耐张绝缘子串包含了较多的部件,不同部件之间存在相互运动,分析金具之间的约束关系非常重要。采用接触算法计算各金具之间的相互运动关系,模拟结果更为准确。但是以现有的有限元计算效率采用接触算法只适合模拟两个或者几个金具模型,对于复杂的耐张串模型则计算收敛非常困难。为了既能模拟金具之间的相互运动又能提高计算效率,采用了“Hinge”和“Join+Universal”等连接关系[16-17]模拟金具之间的相对运动,金具之间的约束关系设置如图 8所示。对于后期的精细化仿真,则可以选择其中危险的金具进行单独分析,这时可以采用接触算法进行仿真。
|
| 图 8 金具之间的约束关系设置 Figure 8 Constraint relationship settings between fittings |
本文选取U形挂环作为研究对象分析接触计算方法和连接单元计算方法之间的区别。U形挂环上端有两个孔,当中间穿入圆柱体后,U形挂环可以绕着圆柱体转动。进行有限元仿真时,首先设置圆柱和U形挂环的两个孔接触,加载后U形挂环的应力分布情况如图 9(a)所示。将中间圆柱体和U形挂环两个孔设置铰链(Hinge)连接单元,可以实现相同的转动。施加相同的荷载后,应力分布情况如图 9(b)所示,通过切片对比两者的应力分布情况可以看出,两者的最大应力误差只有3%。对于U形挂环下端则和另外一个U形挂环相连,此时采用“Join+ Universal”属性的连接单元。同理,设置两个U形挂环,这两个挂环接触时计算得到的应力分布情况如图 9(c)所示。如果采用连接单元,其应力分布情况如图 9(d)所示。通过切片对比两者的应力分布可以看出,两者的最大应力误差只有1%。对比接触和连接单元仿真可以看出,如果选取合适的连接单元既可以满足金具之间相互转动的计算需求,又可以提升计算效率。

|
| 图 9 U形挂环耦合面(虚线框标记)的验证结果 Figure 9 Verification results of U-shaped hanging ring coupling surface (marked with dashed boxes) |
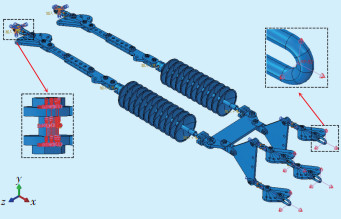
根据图 1可知悬垂绝缘子串一端连接到杆塔上,另一端与导线相连接。考虑杆塔结构结实,忽略杆塔运动对耐张绝缘子串的影响,因此与杆塔相连接的位置设置为铰链约束,即耐张绝缘子串可以绕着该点产生旋转。绝缘子串另一端与导线相连,导线受到随机风荷载作用会产生变化张力。为了提高计算效率本文将导线的张力直接施加到耐张串,计算耐张串在最大张力的作用下各金具的应力分布情况。如图 10所示,每3个红色箭头代表 1条导线的张力在3个坐标轴上的分量。将图 3得到的导线张力施加到绝缘子串上,具体方向见图 10中的红色箭头。
|
| 图 10 边界条件及载荷 Figure 10 Boundary conditions and loads |
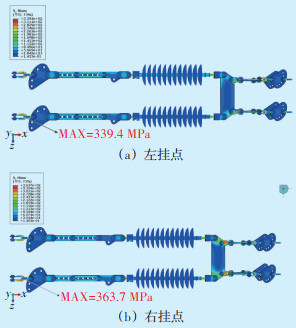
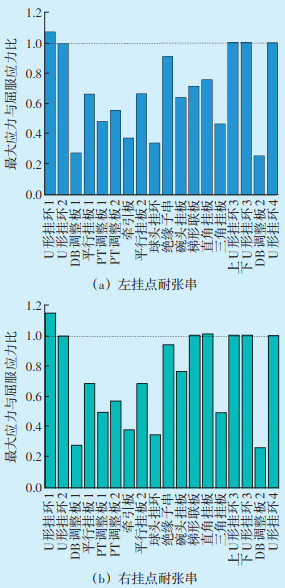
将图 2的导线张力施加到耐张串上得到金具的应力云图见图 11。可以看出,在随机风荷载作用下左、右挂点耐张串最大应力出现的位置均为U形挂环,最大应力值分别为363.7 MPa、339.4 MPa。耐张串中各金具的最大应力与屈服应力的比值如图 12所示,右挂点耐张串梯形联板、直角挂板以及5个U形挂环均超过了屈服强度,绝缘子串最大应力与屈服应力的比值分别为0.95,绝缘子串也属危险部件,其余部件相对较为安全。左挂点耐张串5个U形挂环同样超过了材料的屈服应力,而相应的绝缘子串最大应力与屈服应力的比值为0.91,相对比较危险,其余部件应力值相对较小。从总体结果来看,悬挂到高点即右侧的耐张串超过屈服应力的部件数量大于左侧的绝缘子串,说明悬挂在高点的绝缘子串金具更易损坏。
|
| 图 11 耐张串整体模型应力云图 Figure 11 Stress nephogram of the overall model of strain insulator string |
|
| 图 12 各部件最大应力与屈服应力比值 Figure 12 Ratio of maximum stress to yield stress of each part |
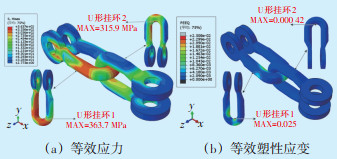
考虑到随机风荷载作用下右侧U形挂环的应力大于左侧的U形挂环的应力,因此图 13—15给出右侧U形挂环的局部应力分布情况。从图 13可以看出U形挂环的最大应力出现在两个挂环接触的位置,U形挂环2应力最大值为315.6 MPa,U形挂环1最大应力值为363.7 MPa,均超过了屈服应力,即两个挂环接触的区域容易发生屈服。除了接触区域发生较大的应力,接触区域之外也有显著的红色,说明U形挂环其他区域也有容易发生破坏的位置。
|
| 图 13 U形挂环1、2应力、应变分布(右挂点) Figure 13 Stress and strain distribution of U-shaped hanging ring 1 and 2 (right hanging point) |
|
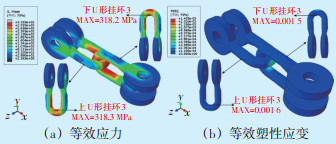
| 图 14 U形挂环3应力、应变分布(右挂点) Figure 14 U-shaped hanging ring 3 stress and strain distribution (right hanging point) |
|
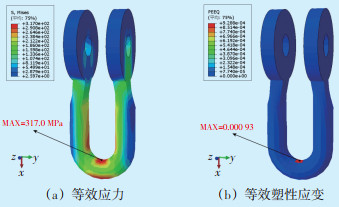
| 图 15 U形挂环4应力、应变分布(右挂点) Figure 15 U-shaped hanging ring 4 stress and strain distribution (right hanging point) |
上U形挂环的最大应力值为318.3 MPa,下U形挂环的最大应力值为318.2 MPa,均在两个挂环的接触区域。U形挂环4最大应力值317 MPa。对比图 13—15可以看出,对于U形挂环,最大应力均出现在两个挂环的接触区域。在随机风荷载作用下导线会产生较大变化张力,施加到金具上也会出现较大的应力波动,而U形挂环在交变应力波动影响下,会产生局部较大磨损,进而引起破坏,如图 16所示。可以看出,即使未发生严重磨损,U形挂环也容易损坏,这与图 13—15的仿真结果一致,即在U形挂环侧面也有较大的应力。

|
| 图 16 U形挂环磨损及破坏 Figure 16 Wear and damage of U-shaped hanging ring |
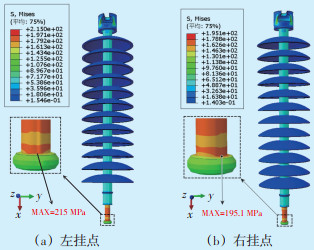
图 17为绝缘子串的应力云图,最大应力发生在球头部位,为215 MPa,接近屈服强度,因此绝缘子串的球头部位也是容易发生破坏的一个部位,在今后的线路运维中需要进行更多的关注。在现有的线路中也存在球头破坏的情况,如图 18所示。
|
| 图 17 绝缘子串应力分布 Figure 17 Stress distribution of strain insulator strings |

|
| 图 18 绝缘子串球头破坏 Figure 18 Damaged ball joint of strain insulator string |
本文采用谐波叠加法模拟了沿线路方向的随机风,将随机风转换为随机风荷载施加到导线上得到导线的最大张力,然后通过耐张串的精细有限元模型进行仿真,得到各金具的应力分布情况。最终的仿真结果表明最容易发生破坏的金具为U形挂环,在其接触区域易发生磨损。其次,直角挂板和梯形联板在左、右挂点表现出了不同的安全性,高悬挂点处更容易发生破坏。此外绝缘子串球头部位的应力较大,在受到极端荷载作用时容易断裂。本文提出了一种计算随机风荷载作用下耐张串金具有限元仿真的方法,根据计算结果可以对金具的安全性能进行评估,对于保障线路安全运行减少线路故障具有重要意义。
| [1] |
陈浩, 田峰, 张涛, 等. 110 kV输电线路悬式绝缘子钢脚断裂原因分析[J].
内蒙古电力技术, 2022, 40(6): 37-40 CHEN Hao, TIAN Feng, ZHANG Tao, et al. Fracture Cause Analysis of Steel Foot of Suspension Insulator Used in 110 kV Transmission Line[J]. Inner Mongolia Electric Power, 2022, 40(6): 37-40 (  0) 0)
|
| [2] |
黄双得. 110 kV线路连接金具断裂原因分析及防范措施[J].
电工技术, 2021(17): 125-127 HUANG Shuangde. Cause Analysis and Preventive Measures of 110 kV Transmission Line Connection Fittings Fracture[J]. Electric Engineering, 2021(17): 125-127 (  0) 0)
|
| [3] |
朱迪锋, 许杨勇, 吴坤祥, 等. 500 kV输电线路工作接地线挂设处导线断裂原因分析[J].
内蒙古电力技术, 2018, 36(3): 43-46 ZHU Difeng, XU Yangyong, WU Kunxiang, et al. Cause Analysis of 500 kV Transmission Line Fracture at Grounding Wire Hanging Point[J]. Inner Mongolia Electric Power, 2018, 36(3): 43-46 (  0) 0)
|
| [4] |
王旭东. 输电线路防振锤线夹附近导线力学特性研究[D]. 北京: 华北电力大学, 2021.
(  0) 0)
|
| [5] |
赵建利, 贾新民, 张捷, 等. 架空输电线路间隔棒阻尼失效及铰链销脱落退出分析[J].
内蒙古电力技术, 2020, 38(5): 25-29 ZHAO Jianli, JIA Xinmin, ZHANG Jie, et al. Defect Analysis of Damping Failure and Hinge Pin Exit for Quad-Bundled Spacers of Overhead Transmission Line[J]. Inner Mongolia Electric Power, 2020, 38(5): 25-29 (  0) 0)
|
| [6] |
吴穹. 500 kV超高压输电线路金具挂环断裂原因及预防措施[J].
电工技术, 2020(13): 113-114 WU Qiong. Causes and Preventive Measures of Fracture of Metal Hanging Rings on 500 kV EHV Transmission Line[J]. Electric Engineering, 2020(13): 113-114 (  0) 0)
|
| [7] |
王松臣, 李新梅, 王晓辉, 等. 连接金具U型环的失效分析及预防[J].
热加工工艺, 2022, 51(4)146-148, 151 WANG Songchen, LI Xinmei, WANG Xiaohui, et al. Failure Analysis and Prevention of U - ring of Link Hardware[J]. Hot Working Technology, 2022, 51(4)146-148, 151 (  0) 0)
|
| [8] |
罗淞, 仲昭峰, 秦澔澔, 等. 风沙区域输电线路直角挂板组件磨损分析[J].
电力安全技术, 2021, 23(5): 20-24 LUO Song, ZHONG Zhaofeng, QIN Haohao, et al. Abrasion Analysis of Right-angle Hanging Board Assemblies of Transmission Lines in Wirdy Desert Areas[J]. Electric Safety Technology, 2021, 23(5): 20-24 (  0) 0)
|
| [9] |
李晓光, 龚浩, 金铭, 等. 沙漠区域输电线路绝缘子风偏运动分析[J].
湖北大学学报(自然科学版), 2021, 43(1): 91-95 LI Xiaoguang, GONG Hao, JIN Ming, et al. Wind deviation motion spectrum analysis of insulators in transmission lines of desert areas[J]. Journal of Hubei University (Natural Science Edition), 2021, 43(1): 91-95 (  0) 0)
|
| [10] |
牛格图, 陈岩, 李林孝, 等. 随机风作用下同塔四回输电杆塔安全性分析[J].
重庆大学学报, 2022, 45(12): 103-115 NIU Getu, CHEN Yan, LI Linxiao, et al. Analysis on safety of four circuit transmission line tower under stochastic wind field[J]. Journal of Chongqing University, 2022, 45(12): 103-115 (  0) 0)
|
| [11] |
杨雄骏, 黄金山, 张建国, 等. 基于插值与降维方法的输电塔线体系随机脉动风场有效模拟[J].
振动与冲击, 2021, 40(9): 77-83 YANG Xiongjun, HUANG Jinshan, ZHANG Jianguo, et al. Effective simulation of stochastic fluctuating wind field of transmission tower - line system based on interpolation and dimension reduction method[J]. Journal of Vibration and Shock, 2021, 40(9): 77-83 (  0) 0)
|
| [12] |
牛海军, 司佳钧, 周立宪, 等. 特高压输电线路悬垂串金具优化研究[J].
中国电力, 2019, 52(3): 95-101 NIU Haijun, SI Jiajun, ZHOU Lixian, et al. Optimum Research of Suspension String on Ultra High Voltage Transmission Line[J]. Electric Power, 2019, 52(3): 95-101 (  0) 0)
|
| [13] |
黄睿, 刘小会, 李春, 等. 随机风作用下耐张串金具的安全性分析[J].
应用力学学报, 2021, 38(4): 1449-1459 HUANG Rui, LIU Xiaohui, LI Chun, et al. Safety analysis of tension string fittings under random wind[J]. Chinese Journal of Applied Mechanics, 2021, 38(4): 1449-1459 (  0) 0)
|
| [14] |
李春, 刘小会, 黄睿, 等. 输电线脱冰过程中耐张串金具的受力仿真分析[J].
图学学报, 2021, 42(2): 279-288 LI Chun, LIU Xiaohui, HUANG Rui, et al. Simulation analysis of stress in power fitting for strain insulator - string following ice shedding from cables[J]. Journal of Graphics, 2021, 42(2): 279-288 (  0) 0)
|
| [15] |
黄飞. 极端环境下输电线路动力响应及金具仿真分析[D]. 重庆: 重庆交通大学, 2021.
(  0) 0)
|
| [16] |
郎超. 脱冰条件下特高压直流线路耐张联板动态特性研究[D]. 北京: 华北电力大学, 2020.
(  0) 0)
|
| [17] |
Cai D, Yan B, Gao Y, et al. Stability Behavior and Optimization of Tension Plates in Transmission Lines in Heavy Ice Zones[J].
IEEE Transactions on Power Delivery, 2021 (  0) 0)
|
 2023, Vol. 41
2023, Vol. 41