我国新能源资源储量丰富,积极发展新能源发电,是我国调整能源结构、保护环境、应对气候变化、转变经济发展方式和实现可持续发展的一项战略选择[1]。近几年,我国新能源电力发展迅猛,截至2020年底,我国新能源装机容量累计达5.3亿kW,在某些区域甚至已出现新能源规模化并网[2]。然而我国的新能源分布与能源需求大致呈逆向,大量新能源并入电网后势必要进行远距离输送。以风能和太阳能为代表的新能源具有很强的随机性和间歇性,新能源基地的电力电子设备具有很强的非线性,当庞大数量的新能源接入电网后,这些特性也同时被引入电网,对电网的安全稳定构成威胁。
当前,新能源规模化并网引发的稳定问题已引起国内外的广泛关注,文献[3]探讨了间歇性电源点静态安全域限制下的最大有功容量,通过匹配最佳集线阻抗比实现风电场的安全外送;文献[4]研究了电网事故时的频率应急响应,通过调节需求响应抑制输出功率急剧波动,但该方法启动较慢且需要设置响应负荷;文献[5-7]分析了新能源并网后的概率潮流问题,通过细化概率范围改进潮流计算方法,但并未深入探讨电网遭受风险的应急举措;文献[8] 提出了一种利用抗差理论进行电网状态估计的方法,但该方法计算量较大,目前尚不能实现大数据的实时估测;文献[9-11]研究了大电网安全性评估的复杂性理论和电网状态评估的风险防范管理体系,但也没有开展风险应急研究。
综上,新能源富集电网迫切需要一种快速精准的电网状态估计方法以及与其匹配的智能应急调度策略来保障安全和稳定。本文在汲取国内外研究成果的基础上,通过深入分析电网的运行状态,从电网应急的角度提出一种适用于新能源富集电网的状态估计方法,通过快、精、准地评估电网运行信息,第一时间感知电网存在的风险,自动启用应急调度手段,及时消除规模化新能源带来的稳定问题,保障电网的安全和稳定。
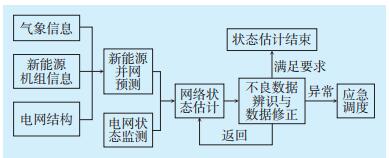
1 新能源富集电网状态估计 1.1 电网状态估计功能流程规模化新能源的电网状态估计功能流程见图 1。在传统电网中通常“以发定用”,若要得到理想的状态估计结果,首先应从精准的发电预测开始。
|
| 图 1 电网状态估计功能流程图 Figure 1 Functional process of power grid state estimation |
调度大信息是电力数据库中的一种广域信息源,不仅包括已知的电网电气量信息和非电气量信息(气象、地质、设备状态等),还包括与电力生产相关的音频、视频等动态信息[12]。
利用调度大信息中含有诸多影响新能源并网的有用信息,如气象和地质信息、新能源机组、电网实时数据以及电力需求等,提前对新能源并网情况进行精确预测,根据实际情况制订灵活的短时发电计划和电网可调节裕度等,进而减少因客观因素约束造成的电网稳定性事件。
1.3 电网状态分层估计我国的大型新能源基地通常都处在电网结末端,当规模化新能源并网传输时,除部分有专属输送通道外,其余均直接或间接接入附近的220 kV变电站,再以220 kV电压等级汇入超高压或特高压网络向外传输。
考虑到新能源电力变动较为频繁且跨越多电压等级电网,状态估计节点数据量大且繁杂,进行电网状态计算时,为了提升电网状态估计的速度,缩短网络分析和决策时间,可按照电压等级人为划分电网层级,在多层网络中同步进行状态估算。
另外在进行电网状态分析时,为提升计算速度,可将网内节点按照作用分类,将某些非重要节点进行合并或忽略,免去一些不必要的计算,只考虑网络传输中重要节点的运行信息,增加电网感知风险的灵敏度。当电网出现稳定偏差时,系统会第一时间察觉,为处理问题节省时间,避免事态恶化。
1.4 重要断面潮流裕度估计电网正常运行中,通过估计重要断面的运行状态,可及时调整电网的动态潮流,第一时间消除电网存在的隐性风险。在含有规模化新能源的电力网络中,大量新能源的存在增加了断面输送限制或线路N-1故障的概率。引入电网断面作为约束条件可增强电网的敏感度,保证该网络和相邻网络的供电可靠性。
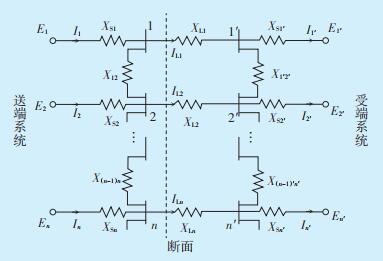
将电网断面单独列出分析,等值模型结构如图 2所示。图中,混杂新能源的电力潮流从系统送端端口输入网络,经断面1,2,…,n进行传输至受端端口。根据系统断面潮流平衡方程有:
|
| 图 2 电网断面等值模型结构示意图 Figure 2 Equivalent model structure of power grid section 图中:E1,E2,…,En—送端系统节点1,2,…,n的电势;E1′,E2′,…,En′—受端系统节点1′,2′,…,n′的电势;I1,I2,…,In—送端系统节点1,2,…,n的电流;IL1,IL2,…,ILn—电网断面第1,2,…,n支路的电流;XS1,XS2,…,XSn—送端系统节点1,2,…,n的源端阻抗;XS1′,XS2′,…,XSn′—受端系统节点1′,2′,…,n′的负载端阻抗;XL1,XL2,…,XLn—电网断面第1,2,…,n支路的支路阻抗;X12,…,X(n-1)n—送端n-1节点与n节点间的阻抗;X1′2′,…,X(n-1)′n′—受端n-1节点与n节点间的阻抗。 |
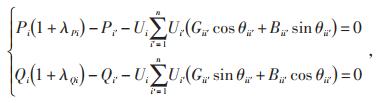
|
(1) |
式中:Pi—送端系统节点i的有功功率;
Qi—送端系统节点i的无功功率;
Pi′ —受端系统节点i′的有功功率;
Qi′—受端系统节点i′的无功功率;
λPi—送端节点i的有功功率增长因子;
λQi—送端节点i的无功功率增长因子;
Ui—送端系统节点i的电压;
Ui′—受端系统节点i′的电压;
Gii′—送端系统节点i与受端系统节点i′间的电导;
Bii′—送端系统节点i与受端系统节点i′间的电纳;
θii′—送端系统节点i与受端系统节点i′间的电压相角。
根据内点法求极值,可得出目标函数λ的最小值λmin=λPi=λQi,断面潮流增量最小,对应系统送端负荷的最大电压临界点,此时,系统断面裕度L为:
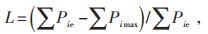
|
(2) |
式中:Pimax—节点i在电压极值点处的送端有功功率;
Pie—节点i的最大有功功率。
将系统断面的稳定控制极限有功功率代入式(2)计算出系统断面裕度下限Lmin。这样,在系统运行中,无论是新能源侧负荷变动或者送端系统发生N-1故障,只要系统重要断面的系统裕度值L>Lmin,且负荷裕度变化率在限定范围内,则可判断系统断面稳定且能抵抗扰动风险;若L<Lmin,则可判断系统断面超过最大负荷裕度,需要立即减少送端进入断面潮流;若L≥Lmin,但负荷裕度变化趋近断面最小裕度,则需及时调节新能源侧动态潮流,增加断面裕度,保证系统稳定运行。
2 超松弛迭代修正的状态估计模型及时调节电网重要断面潮流可避免电网遭受重创。在实际运行过程中,为避免出现事故时电网发生重大调整,需要在网内加入各主要节点定时的状态估计,通过综合各节点当前状态量及变化趋势及时进行系统风险甄别。为保证电网状态估算快速、准确,选用超松弛迭代修正的最小二乘法作为网内节点状态的估计方法。
2.1 状态估计前处理考虑到规模化新能源并网系统的计算量,同时便于快速分析网络稳定性,在状态估计前需将系统进行如下处理。
(1)区域内新能源出力往往具有很强的趋同性,可利用调度大信息区间估计新能源潮流注入量,以减小规模化新能源波动引起的计算误差;
(2)按照电压等级将网络结构人为分层,再按照设定的层级优先度进入相应的网层进行节点状态估计。
2.2 利用最小二乘法估计节点变量假设网间某点潮流注入量实际值为z,估计值为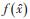
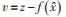
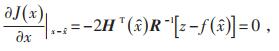
|
(3) |
其中:
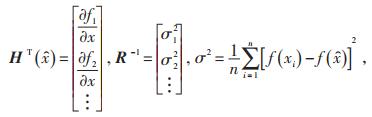
|
式中:n—节点数量;
σ2—实际值与估计值的方差;
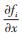
利用超松弛迭代公式修正估计值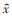
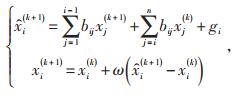
|
(4) |
式中:ω—松弛因子;
xi(k)—节点i第k次修正得到的数值;
xj(k)—节点j第k次修正得到的数值;
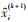
bij—节点i与节点j间的节点参数;
gi—关于节点i的某一常量。
用树枝-连枝法构建系统网络,由于在新能源富集电网中节点自导纳远大于节点注入功率,构建参数矩阵可严格对角占优,所以超松弛法修正的系统收敛,可得到收敛值。
在电力网络中,加入网络节点潮流、历史状态及控制变量等式约束:
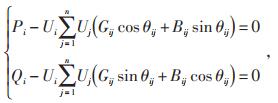
|
(5) |
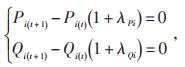
|
(6) |
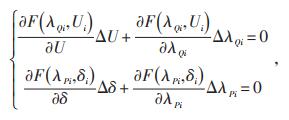
|
(7) |
式中:Pi(t)—t时刻节点i的有功功率;
Qi(t)—t时刻节点i的无功功率;
Uj—节点j的电压;
Gij—节点i与节点j间的电导;
Bij—节点i与节点j间的电纳;
θij—节点i与节点j间的电压相角;
δi—节点i的功角;
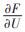
ΔU—电压变量;
Δδ—功角变量。
同时对于节点i加入节点电流等式约束和功率不等式约束:
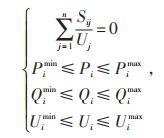
|
(8) |
式中:Sij—节点i与节点j之间的视在功率;
Pimin—节点i有功功率的最小值;
Qimin—节点i无功功率的最小值;
Uimin—节点i电压的最小值;
Pimax —节点i有功功率的最大值;
Qimax—节点i无功功率的最大值;
Uimax—节点i电压的最大值。
在构建模型中,因获取量测数量大于量测变量(n>m,且各式不相关),可知构建系统状态满秩、可观。将各层网络中的节点分别归类,通过状态估计模型多次迭代逐次得到相应的估计值:
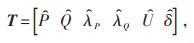
|
(9) |
式中:T—变量估计值的状态向量;
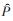
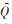
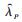
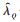
Ȗ—电压量的估计值;
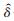
在庞大的系统状态估计计算时,难免会有不良数据出现,为了保证数据估算可靠,可在数据估算模块加入数据修正功能,具体如下。
(1)系统辨识数据时,可通过两个或两个以上非关联可靠数据进行比对分析,当同时认定数据异常时,可判断所估算数据不良;
(2)每隔一定时间发现有不良数据,利用节点或最近节点的SCADA数据信息做辨识比对修正;
(3)当辨识到由于计算引起某数值越限时,为避免扰乱系统整体估算,可将该节点类型转换(PV、PQ转换),利用一个周期的正确数据进行修正。
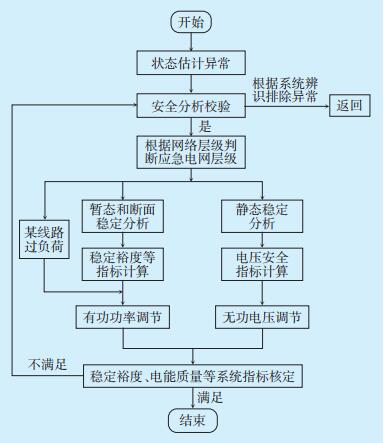
3 智能调度应对策略在规模化新能源输送的过程中,状态估计模块连续三次计算得出某点状态异常,则应及时启动应急调度模块进行系统智能修正。具体的电网智能调度应急流程如图 3所示。
|
| 图 3 智能调度应急功能流程图 Figure 3 Functional process of intelligent dispatching emergency |
电网状态估计监测到异常,首先启动智能调度功能模块进行电网状态安全分析校验。系统辨识子模块根据系统动态信息检验到系统正常,功能返回;若检查到电网状态发生异常,则进一步锁定异常点来源的电压层级,即锁定发生异常的局部电网,缩小调整的波及面。
锁定故障电压层级后,在相应层中启动电网稳定分析子模块,并根据电网中的相关数据指标进行判断。电网某节点电压越限,并超过安全裕度,电网智能调整子模块启动无功电压调节功能,锁定周边无功发生设备,满足调节条件后按优先等级进行无功电压调节,直至电网静态稳定满足指标后返回。
若状态估计数据中某断面稳定裕度越过指标值,电网智能调整子模块启动电网有功功率调节功能,按照计算的裕度、电网当前的状况及调节的优先顺序,逐步采取安全自动装置切机、切负荷或转移负荷等方式进行系统有功功率调节,直至电网稳定裕度满足指标后返回。
当电网设备出现穿越性故障或输电线路出现瞬时故障时,线路重合成功或系统短时间内发生潮流转移,此时电网应根据实际情况判断不做出调整,自适应躲过电网自调整时间[13-18]。
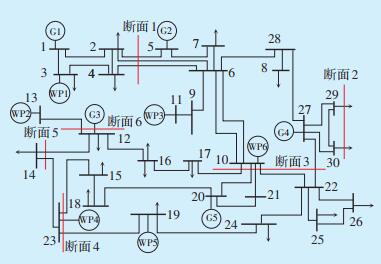
4 算例分析 4.1 算例简介选用某电网简化的30节点系统进行算例分析。以IEEE-30系统为基础,选取主电网(500 kV、220 kV电压等级)30个代表性节点,按照电网拓扑由西向东走向对应节点1至节点14匹配,构建电网简化的30节点系统,见图 4。
|
| 图 4 某电网简化的30节点系统 Figure 4 Simplified 30-node system of some power grid 图中:G1,G2,…,G5—传统能源发电厂;WP1,WP2,…,WP6—并网的新能源基地;节点6、9、10、12、14、15、16、17、18、19、20、21、22、23、27、28—500 kV电压等级变电站;节点1、2、3、4、5、7、8、11、13、24、25、26、29、30—220 kV电压等级变电站。 |
在图 4所示的电网系统中,规模化新能源电力从网内各并网节点向节点14输送,为保证新能源电力的安全输送,在电能输送沿途共设置6个重要断面作为电网安全重要监视面,即断面1的KD潮流断面(220 kV),断面2的EW潮流断面(220 kV),断面3的HB潮流断面(500 kV),断面4的HF潮流断面(500 kV),断面5的外送电流潮流断面(500 kV)和断面6的QY潮流断面(220 kV)。
4.2 网络分层监测重要断面的稳定程度为快速计电网稳定程度,按照网络分层原则,将简化30节点系统自动划分为500 kV和220 kV电压等级电网,并在各自电网中进行重要断面稳定性分析。
图 4中,断面3、4、5为500 kV电压等级重要断面,断面1、2、6为220 kV电压等级重要断面,由于断面4和6是断面5的潮流源,对断面5的影响较大,所以断面4和6的稳定裕度会直接影响断面5的稳定;同样,断面1是断面2和3的潮流源,断面1的稳定裕度会直接影响断面2和3的稳定。因此根据源侧断面优先的原则,分别在两层电网中按照次序同时计算,如220 kV网络中进行断面1、2、6的计算,同时在500 kV网络中进行断面3、4、5的计算,当发现某断面异常后,可联合两层电网锁定局部网络节点迅速进行智能调整。
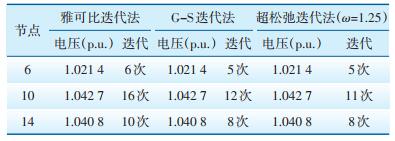
4.3 超松弛迭代法估算验证电网安全性能选用超松弛迭代法作为网内节点的状态估算方法,为证明超松弛迭代法的估算性能,选取3个代表节点(节点6、10、14),分别用雅可比迭代法、Gai-si_Saideer(G-S)迭代法和超松弛迭代法进行节点电压比对估算(精度取),结果如表 1所示。
| 表 1 3种迭代法节点估计数据对比结果 Table 1 Comparison of estimated node data by three iterative methods |
从表 1可以看出,某时刻3个代表节点估算的电压值中,超松弛迭代法(ω取1.25时最优[19]) 的迭代计算次数最少,其次是Gaisi_Saideer迭代法,雅可比迭代法的迭代次数最多。
在计算条件无约束前提下,迭代次数越少,错误率越低。在新能源富集电网的计算中,选取超松弛迭代法作为估算方法数据更准确可靠,满足状态估算要求。
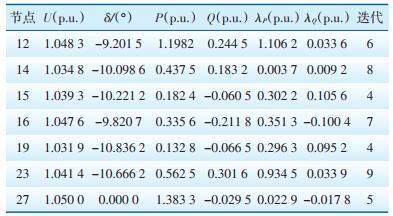
4.4 断面稳定的智能调度验证调整测试系统中WP2、WP4、WP5满出力发电及区域电网的运行方式,模拟断面5稳定裕度不足的情况。此时系统估算的部分节点数据见表 2。
| 表 2 断面5相关节点状态估计数据 Table 2 State estimation data of relevant nodes of section 5 |
表 2中节点均为500 kV变电站,节点14是断面5唯一的能源输出点。设定断面5的输送最大有功功率为4500 MW,系统基准容量为10 000 MW,计算断面5的稳定裕度为:
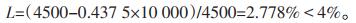
|
经计算,断面5的稳定裕度值小于额定裕度值4%,启动智能调度模块进行动态调节,流程如下:
(1)锁定调节的应急区域;
(2)按照预定优先级转移负荷,将节点12的部分负荷倒至节点16接带,节点23的部分负荷倒至节点15和19接带(从表 2数据及图 4可知,节点15、16、19负荷未满,可受),来减轻断面4的承载压力;
(3)动态调整电厂G3和G5出力并保证相关新能源电厂出力,直至断面5的稳定裕度逐步恢复至额定值以上。
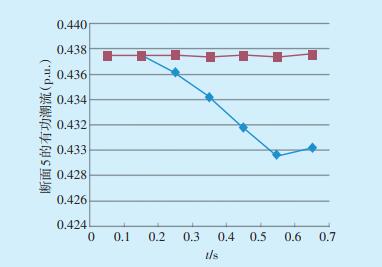
模拟断面5有无智能调度应急调节,仿真节点14输出有功潮流变化如图 5所示。经过断面5的所有有功功率经由节点14输出,节点14输出有功功率即为断面5的有功潮流。
|
图 5 断面5有无智能调度调节的有功潮流对比
Figure 5 Comparison of active power flow for section 5 with and without intelligent dispatching regulation
图中: -有智能调度应急调节; -有智能调度应急调节; -无智能调度应急调节。 -无智能调度应急调节。
|
根据图 5,调节后断面5的稳定裕度为:
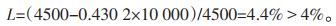
|
经过计算,调节后断面5的稳定裕度满足系统要求,智能调度应急功能返回,系统调节用时为0.6~ 0.7 s。
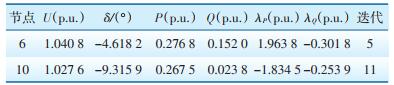
4.5 重要线路突发N-1故障时的功能验证模拟系统中节点6与10之间的线路突发永久性接地故障(N-1故障),利用超松弛迭代修正的状态估计方法进行系统估算,结果如表 3所示。
| 表 3 线路6—10突发N-1永久性故障的状态估计数据 Table 3 State estimation data of line 6-10 N-1 permanent fault |
根据表 3与表 1的数据对比可以看出,当线路6—10发生永久性接地故障时,节点6的电压值会变大,节点10的电压值会变小。
结合相关断面和节点的估算数据,系统会综合判明故障类型及影响区域,第一时间发出警报。智能调度系统在收到故障警报后,瞬时开放接收继电保护和故障远传信息,随即启动智能调度应急功能进行调节,具体流程如下:
(1)锁定节点6和10的相关断面和节点,进行计算;
(2)根据计算按照预定优先级减小电厂G1、WP1或G2的发电出力,调节断面1的潮流裕度;
(3)同时根据预定优先级增加电厂G3、WP6或G5的发电出力,保证节点16与17的负荷供应;
(4)适当调节节点6与10的无功功率,保证两节点的电压值满足系统要求。
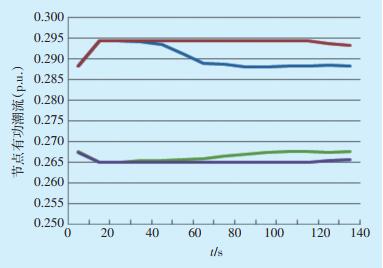
调节过程中相邻节点7和17输入的有功潮流数据变化曲线如图 6所示。
|
图 6 突发N-1永久性故障时有无智能调度方案对比
Figure 6 Comparison of intelligent dispatching schemes in case of sudden N-1 permanent fault
图中: -有智能调节的节点7; -有智能调节的节点7; —无智能调节的节点7; —无智能调节的节点7; —有智能调节的节点17; —有智能调节的节点17; -无智能调节的节点17。 -无智能调节的节点17。
|
根据图 6中节点7和17的有功潮流显示,分层网络通过状态估计监测到线路6—10突发N-1永久性故障后,在约5 s时可以看到智能调度应急调节的节点7和17有功潮流发生变化,经过约120 s,节点7和17的有功潮流恢复至故障前数值,而无智能调节功能的节点7和17有功潮流此时才开始发生变化。通过此次对比试验可以看到通过选用的电网状态估计及智能调度策略可以减少系统突发故障时的调节时间,对于保障重要节点的供电可靠性及电网安全稳定性都能起到积极的作用。
5 结束语新能源规模化并网已成趋势,本文提出在对并网新能源精准估测的基础上,通过电网重要断面及分层网络使用超松弛迭代修正的监测方法提前感知电网的不良状况,第一时间启用智能应急调度策略应对新能源规模化并网而引发的各种电网问题,将电网遭受的冲击降至最小。通过算例分析可知,本文提出的电网状态估计方法及智能调度策略对于保证新能源富集电网的安全稳定可以起到明显的作用,具有实用性。
| [1] |
舒印彪, 张智刚, 郭剑波, 等. 新能源消纳关键因素分析及解决措施研究[J].
中国电机工程学报, 2017, 37(1): 1-8 SHU Yinbiao, ZHANG Zhigang, GUO Jianbo, et al. Study on key factors and solution of renewable energy accommodation[J]. Proceedings of the CSEE, 2017, 37(1): 1-8 (  0) 0)
|
| [2] |
王晓晨, 金艳鸣, 张晋芳, 等. 考虑新能源大规模发展的差异化综合效益评价模型[J].
中国电力, 2018, 51(10): 178-184 WANG Xiaochen, JIN Yanming, ZHANG Jinfang, et al. A comprehensive evaluation model for power system with large-scale new energy considering regional differences[J]. Electric Power, 2018, 51(10): 178-184 (  0) 0)
|
| [3] |
郭旭, 王海风. 静态安全域限制下的风电场最大外送有功容量[J].
现代电力, 2021, 38(1): 94-100 GUO Xu, WANG Haifeng. Maximum outgoing active power capacity of wind farm under static security do-main[J]. Modern Electric Power, 2021, 38(1): 94-100 (  0) 0)
|
| [4] |
Uehara T, Matayoshi H, Ludin G A, et al. System frequency control using emergency demand response in power systems with large-scale Renewable Energy Sources[C]//Tencon IEEE Region 10 Conference. IEEE, 2016: 534-537.
(  0) 0)
|
| [5] |
柳志航, 卫志农, 高昇宇, 等. 源-荷互动环境下含高比例风电并网的自适应线性化概率潮流计算[J].
电网技术, 2019, 43(11): 3926-3934 LIU Zhihang, WEI Zhinong, GAO Shengyu, et al. Adaptive-linearized probabilistic power flow calculation for power grid integrated with high proportion wind power in source-load interactive environment[J]. Power System Technology, 2019, 43(11): 3926-3934 (  0) 0)
|
| [6] |
连浩然, 周保荣, 秦鹏, 等. 基于场景分区的随机潮流解析算法[J].
电网技术, 2017, 41(10): 3153-3160 LIAN Haoran, ZHOU Baorong, QIN Peng, et al. Proba-bilistic power flow analytic algorithm based on scenario partition[J]. Power System Technology, 2017, 41(10): 3153-3160 (  0) 0)
|
| [7] |
Villanueva D, Pazos J L, Feijoo A. Probabilistic load flow including wind power generation[J].
IEEE Transactions on Power Systems, 2011, 26(3): 1659-1667 DOI:10.1109/TPWRS.2010.2096436 (  0) 0)
|
| [8] |
汪杨凯. 基于抗差理论的电力系统状态估计研究[D]. 武汉: 华中科技大学, 2006.
(  0) 0)
|
| [9] |
段贵钟, 秦文萍, 逯瑞鹏, 等. 考虑风电接入与负荷不确定性的静态电压稳定性分析[J].
电力系统保护与控制, 2018, 46(12): 108-114 DUAN Guizhong, QIN Wenping, LU Ruipeng, et al. Static voltage stability analysis considering the wind power and uncertainty of load[J]. Power System Protection and Control, 2018, 46(12): 108-114 (  0) 0)
|
| [10] |
张乾, 胡雪凯, 李均强, 等. 基于复合功角及稳定裕度的多机系统分群研究[J].
智慧电力, 2018, 46(7): 56-60 ZHANG Qian, HU Xuekai, LI Junqiang, et al. Generator groups identification study based on complex angle and stability margin[J]. Smart Power, 2018, 46(7): 56-60 (  0) 0)
|
| [11] |
王敏. 大电网在线安全评估的理论与方法研究[D]. 武汉: 华中科技大学, 2013.
(  0) 0)
|
| [12] |
张连勇. 基于调度大信息的生产预警与风险防范研究[J].
电力安全技术, 2020, 22(1): 1114-14 ZHANG Lianyong. Research on production early warning and risk prevention based on dispatching big information[J]. Electric Safety Technology, 2020, 22(1): 1114-14 (  0) 0)
|
| [13] |
刘爽, 张硕, 郑璐, 等. 基于大数据的电网状态估计精细化分析[J].
电力大数据, 2020, 23(7): 9-15 LIU Shuang, ZHANG Shuo, ZHENG Lu, et al. Fine analysis of power network state estimation based on big datal[J]. Power Systems and Big Data, 2020, 23(7): 9-15 (  0) 0)
|
| [14] |
周艳真, 查显煜, 兰健, 等. 基于数据增强和深度残差网络的电力系统暂态稳定预测[J].
中国电力, 2020, 53(1): 22-31 ZHOU Yanzhen, ZHA Xianyu, LAN Jian, et al. Transient stability prediction of power systems based on deep residual network and data augmentation[J]. Electric Power, 2020, 53(1): 22-31 (  0) 0)
|
| [15] |
王义, 孙永辉, 钟永洁, 等. 计及模型不确定性的发电机动态状态估计方法[J].
电力系统自动化, 2018, 42(21): 77-83 WANG Yi, SUN Yonghui, ZHONG Yongjie, et al. Dynamic state estimation method for generators considering model uncertainties[J]. Automation of Electric Power Systems, 2018, 42(21): 77-83 (  0) 0)
|
| [16] |
唐晓霞, 刘巧华. 用块超松弛迭代法求解不定最小二乘问题[J].
应用数学与计算数学学报, 2015, 29(3): 269-277 TANG Xiaoxia, LIU Qiaohua. Block overrelaxation iterative methods for indefinite least squares problems[J]. Communication on Applied Mathematics and Computation, 2015, 29(3): 269-277 (  0) 0)
|
| [17] |
田廓, 董文杰. 需求侧响应及输电约束条件下大规模新能源发电并网机组组合模型[J].
智慧电力, 2019, 47(1)54-58, 71 TIAN Kuo, DONG Wenjie. Unit commitment model of large scale new energy generation integrated into grid with demand response resources based on price and transmission capacity constraints[J]. Smart Power, 2019, 47(1)54-58, 71 (  0) 0)
|
| [18] |
魏俊姣. 防连锁跳闸的脆弱线路输电断面搜索与控制策略研究[D]. 北京: 华北电力大学, 2015.
(  0) 0)
|
| [19] |
杜蕙, 林涛, 陈汝斯, 等. 计及电网结构参数变化的有功静态安全域快速构建方法[J].
电力系统自动化, 2020, 44(8): 108-115 DU Hui, LIN Tao, CHEN Rusi, et al. Fast Construction method of active power steady-state security region considering variation of structural parameter in power grid[J]. Automation of Electric Power Systems, 2020, 44(8): 108-115 (  0) 0)
|
 2022, Vol. 40
2022, Vol. 40