BPA仿真软件作为电力系统的一种机电暂态仿真计算工具,已被广泛应用于电网的潮流计算和稳定计算分析中。因其具有仿真规模大、计算速度快、数据稳定性好等优点,在电力系统规划、调度、生产运行中发挥着很大的作用。随着光伏发电规模不断增大,光伏发电出力的波动对电力系统的影响也越来越大,BPA中虽具有光伏发电机电暂态模型,但模型中的参数计算结果与实际光伏逆变器性能响应差异较大,无法精准反映现场机组的实际性能,含光伏发电系统的安全稳定分析准确性受到一定程度的影响。针对新能源机组的动态特性,较多学者结合实测数据开展了参数辨识的方法研究[1-7],结合遗传算法等智能高级算法[8-11],取得了一定进展,但多侧重于方法的提出和验证,没有较好地与电网仿真工具相结合。
为满足大规模光伏并网的安全稳定分析需求,本文对光伏发电系统功率控制输出特性的机电暂态模型控制原理进行研究,提出一种基于电力系统分析软件PSD⁃BPA的光伏逆变器机电暂态功率控制参数辨识方法,采用粒子群算法寻优与仿真模拟相结合,并通过控制器实物硬件在环试验验证了模型参数的准确性,从而提高了对含光伏发电系统的电网安全稳定计算分析的准确性。
1 光伏逆变器机电暂态功率控制模型光伏发电逆变器稳态功率控制主要采用最大功率点跟踪(Maximum Power Point Tracking,MPPT)和恒功率控制,MPPT模式可使光伏阵列输出电压跟踪最大功率点电压,从而输出不同环境下的最大功率[11-18]。恒功率控制模式可使逆变器根据电网的调度实现固定的有功和无功输出,还可根据其输出电压的相角和幅值的变化来对外部电网的功率需求做出响应,同时实现有功和无功的解耦控制,即通过控制逆变器输出电压的相角来调节其输出有功功率,通过控制逆变器输出电压的幅值来调节其输出无功功率。光伏发电单元机电暂态模型稳态功率控制的准确性主要受恒功率控制模式的控制参数影响。
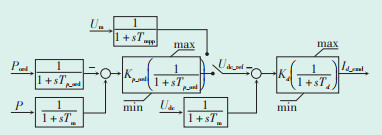
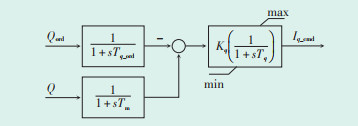
光伏逆变器的控制结构如图 1、图 2所示[19]。功率控制指令从下达到执行,因受通信影响,会有一定的延时,因此在机电暂态模型中通过有功、无功控制指令的延时环节对该部分进行等值。光伏逆变器MPPT跟踪和稳态输出功率电压/电流/功率等电气量采样环节采用惯性环节等值。
|
| 图 1 光伏发电单元有功功率控制结构图 Figure 1 Active power control structure of PV unit |
|
| 图 2 光伏发电单元无功功率控制结构图 Figure 2 Reactive power control structure of PV unit |
光伏逆变器的功率控制采用外环控制,目的是实现PQ解耦控制,其中有功控制通过直流母线电压的闭环控制实现,无功控制通过无功功率的闭环控制实现,外环控制采用比例积分环节,输出量为d、q轴电流的参考值。
光伏逆变器控制模型稳态功率控制待辨识的控制参数包括有功和无功控制环节的PI(比例积分)参数,有功控制比例系数Kp、有功控制时间系数Tp、无功控制比例系数Kq、无功控制时间系数Tq,这些参数的准确性将直接影响其动态特性,需要予以辨识。
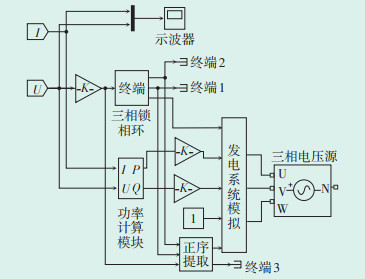
利用MATLAB/Simulink软件搭建光伏并网系统模型,如图 3所示,该模型主要用于光伏功率控制参数的仿真与验证,结合GB/T 32892—2016《光伏发电系统模型及参数测试规程》[19],通过模型及参数的调整开展仿真测试,并与试验数据进行偏差对比分析,考核模型的准确程度。
|
| 图 3 光伏逆变器并网系统模型 Figure 3 Photovoltaic inverter grid connected system model 图中:K—增压系数;I—三相电流;U—三相电压;P—有功功率;Q—无功功率。 |
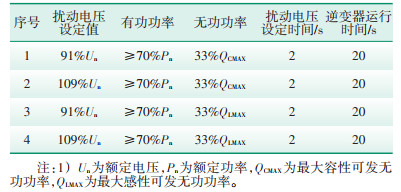
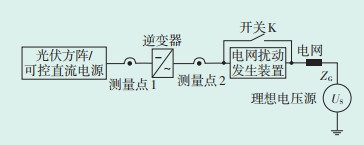
利用RT⁃LAB硬件在环仿真平台,搭建光伏逆变器主电路模型及功率稳态控制参数测试模型(见图 3),并接入某组串式50 kW实物光伏逆变器控制器,开展功率稳态控制参数测试相关电网扰动试验,逆变器模型参数测试示意图如图 4所示。依据表 1要求的电压扰动幅值和时间设置模拟交流侧电网电压扰动参数,完成表中所有试验,测试并记录交流侧电流电压数据。
|
| 图 4 逆变器模型参数测试示意图 Figure 4 Schematic diagram of inverter model parameter test 图中:Us—理想电压;ZG—等值阻抗。 |
| 表 1 交流侧电网扰动试验测试参数1) Table 1 Parameters of grid disturbance test on AC side |
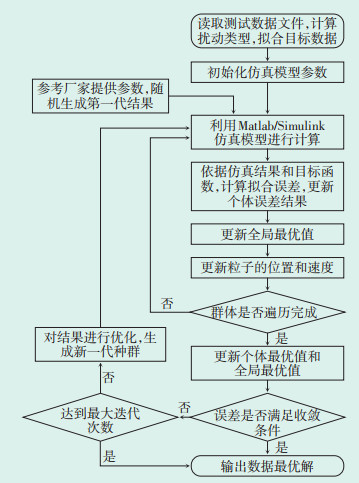
粒子群算法是一种模拟鸟群群体觅食过程中迁徙和群体行为的智能算法,具有鲁棒性好、调整参数较少、收敛速度快等特点,适用于参数辨识中多目标寻优求解的问题[20-23]。将Kp=0.1,TP=0.01,Kq= 0.1,Tq=0.01作为算法迭代的第一代初始值,并设定相应算法的迭代次数、收敛调节、惯性权重、学习因子及参数限制条件。参数辨识采用粒子群算法与仿真模型计算相结合的方法。在电力系统仿真软件中建立与试验系统相同容量、相同参数的仿真模型,设置与试验一致的运行工况和扰动进行仿真,对试验数据和仿真数据进行区间划分和偏差计算,以验证模型参数实测结果的准确性,当误差超出要求后,通过优化算法改变参数组合,并通过不断迭代,直至得到最优参数。其中,迭代次数为100次,误差收敛条件为电压、有功功率、无功功率稳态区间最大偏差允许值满足GB/T 32892—2016的要求,稳态区间最大偏差运行值如表 2所示。得到最优参数后,选取电压、无功电流、无功功率对模型参数的准确性进行验证,具体流程如图 5所示。
| 表 2 稳态区间最大偏差运行值 Table 2 Maximum deviation operating value in steady-state interval |
|
| 图 5 参数辨识迭代示意图 Figure 5 Schematic diagram of parameter identification iteration |
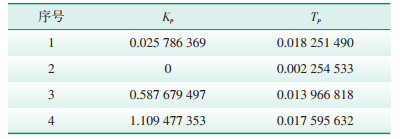
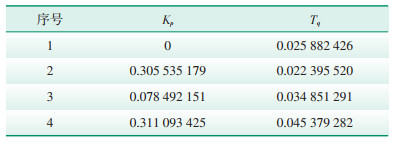
选取稳态区间模型仿真数据与试验数据之间的最大偏差,考核模型的准确程度。所有试验数据处理完后,得到4组辨识的参数满足GB/T 32892— 2016中对偏差的要求[12],如表 3和表 4所示。
| 表 3 有功控制参数辨识结果 Table 3 Identification results of active power control parameters |
| 表 4 无功控制参数辨识结果 Table 4 Identification results of reactive power control parameters |
PSD-BPA中的模型主要通过参数卡填写的方式进行搭建,光伏逆变器模型涉及功率输出特性的参数卡主要有EU卡和EZ卡两部分,EU卡表示正常运行状态下的有功功率控制模型,EZ卡表示正常运行状态下的无功功率控制模型,模型参数填写如图 6所示。

|
| 图 6 PSD⁃BPA中EU卡和EZ卡 Figure 6 EU card and EZ card in PSD-BPA |
KPUDC填写Kp数值,KIUDC填写Kp/Tp数值,KPV填写Kq数值,KPI填写Kq/Tp数值,其余参数根据厂家提供的参数填写。
3.2 BPA模型功率准确性验证在PSD⁃BPA中对4组参数填写形成4种逆变器模型,按照表 1的交流侧电网扰动试验分别对4种模型进行仿真测试,并与RT⁃LAB中实物控制器的试验数据进行对比,验证功率控制BPA模型的准确性。
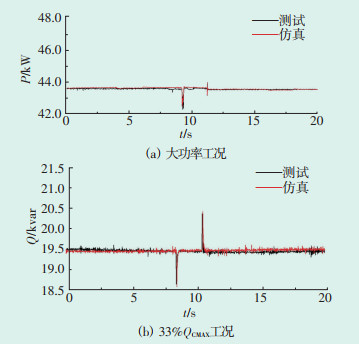
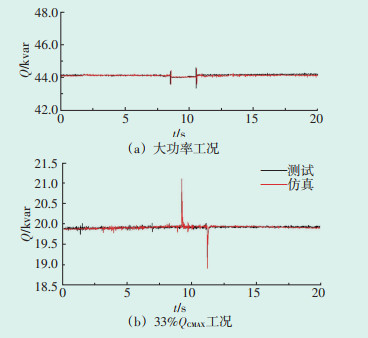
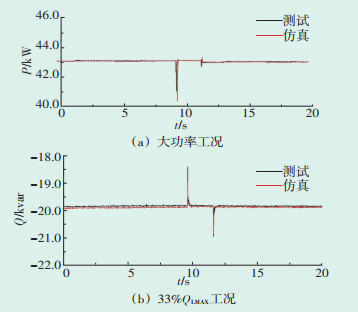
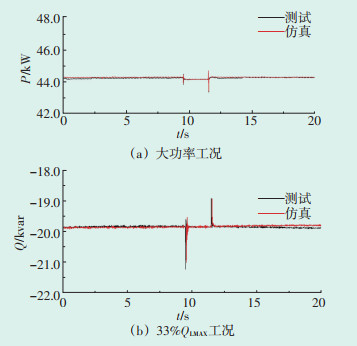
经过试验数据的对比,得出最优参数组合为:Kp=0.587 7,Tp=0.014 0,Kq=0.305 5,Tp=0.022 4,各试验工况下的误差对比曲线如图 7—图 10所示。测试结果表明,BPA中光伏逆变器功率输出特性与RT-LAB半实物仿真结果误差满足GB/T 32892— 2016中对偏差的要求。
|
| 图 7 大功率和33%QCMAX工况下,电压跌落到91%Un的功率变化对比曲线 Figure 7 Comparison curve of power change when voltage drops to 91%Un under high power and 33%QCMAX conditions |
|
| 图 8 大功率和33%QCMAX工况下,电压升高至109%Un的功率变化对比曲线 Figure 8 Comparison curve of power change when voltage rises to 109%Un under high power and 33%QCMAX conditions |
|
| 图 9 大功率和33%QLMAX工况下,电压跌落至91%Un的功率变化对比曲线 Figure 9 Comparison curve of power change when voltage drops to 91%Un under high power and 33%QLMAX conditions |
|
| 图 10 大功率和33%QLMAX工况下,电压升高至109%Un的功率变化对比曲线 Figure 10 Comparison curve of power change when the voltage rises to 109%Un under high power and 33%QLMAX conditions |
本文提出了“粒子群寻优+仿真模拟”相结合的光伏逆变器功率控制参数辨识技术方法,选择典型的光伏逆变器进行了参数辨识及实物控制器试验偏差分析,验证了结果的有效性。该方法解决了逆变器等新能源机组由于核心保密参数无法公开模型参数的技术问题,通过外特性的拟合与评估手段得出了准确的模型参数,可有效提升电网机电暂态仿真分析的动态特性。
| [1] |
刘科研, 盛万兴, 叶学顺, 等. 基于实时仿真硬件在环的光伏逆变控制器参数辨识[J].
科学技术与工程, 2021, 21(24): 10326-10332 LIU Keyan, SHENG Wanxing, YE Xueshun, et al. Parameter Identification of Photovoltaic Inverter Controller Based on Real-time Ssimulation Hardware-in-the-loop[J]. Science Technology and Engineering, 2021, 21(24): 10326-10332 DOI:10.3969/j.issn.1671-1815.2021.24.031 (  0) 0)
|
| [2] |
何廷一, 李胜男, 黄伟, 等. 基于实测参数辨识的双馈风机机电暂态建模研究[J].
云南电力技术, 2020, 48(2)99-102, 110 HE Tingyi, Li Shengnan, HUANG Wei, et al. Parameter Identificantion Method of DFIG Electromechanical Ttransient Modeling Based on Measured Data[J]. Yunnan Electric Power, 2020, 48(2)99-102, 110 DOI:10.3969/j.issn.1006-7345.2020.02.023 (  0) 0)
|
| [3] |
夏天华, 马骏超, 黄弘扬, 等. 基于RTDS硬件在环测试的SVG控制器参数辨识[J].
电力系统保护与控制, 2020, 48(13): 110-116 XIA Tianhua, MA Junchao, HUANG Hongyang, et al. Parameter identification for SVG controller based on RTDS hardware-in-the-loop test[J]. Power System Protection and Control, 2020, 48(13): 110-116 (  0) 0)
|
| [4] |
曹斌, 刘文焯, 原帅, 等. 基于低电压穿越试验的光伏发电系统建模研究[J].
电力系统保护与控制, 2020, 48(18): 146-155 CAO Bin, LIU Wenzhuo, YUAN Shuai, et al. Modeling of photovoltaic power system based on low voltage ride-through test[J]. Power System Protection and Control, 2020, 48(18): 146-155 (  0) 0)
|
| [5] |
徐岩, 靳伟佳, 朱晓荣. 基于遗传粒子群算法的光伏并网逆变器参数辨识[J].
太阳能学报, 2021, 42(7): 103109-109 XU yan, JIN Weijia, ZHU Xiaorong. Parameter identification of photovoltaic grid-connected inverter based on gapso[J]. Acta Energiae Solaris Sinica, 2021, 42(7): 103109-109 (  0) 0)
|
| [6] |
孔祥平, 袁宇波, 阮思烨, 等. 面向故障暂态建模的光伏并网逆变器控制器参数辨识[J].
电力系统保护与控制, 2017, 45(11): 65-72 KONG Xiangping, YUAN Yubo, RUAN Siye, et al. Controller parameter identification of the grid connected PV inverter for fault transient modeling[J]. Power System Protection and Control, 2017, 45(11): 65-72 DOI:10.7667/PSPC160806 (  0) 0)
|
| [7] |
江娜, 曾鹏, 艾波, 等. SPWM逆变器输出共模电压影响因素研究[J].
电力大数据, 2020, 23(9): 74-84 JIANG Na, ZENG Peng, AI Bo, et al. Research on influential factors of output common mode voltage for SPWM inverter[J]. Power Systems and Big Data, 2020, 23(9): 74-84 (  0) 0)
|
| [8] |
张海宁. 基于递推最小二乘算法的逆变器参数辨识[J].
电力科学与工程, 2017, 33(2): 21-27 ZHANG Haining. Parameter identification of inverter based on recursive least square algorithm[J]. Electric Power Science and Engineering, 2017, 33(2): 21-27 DOI:10.3969/j.ISSN.1672-0792.2017.02.004 (  0) 0)
|
| [9] |
张星. 并网光伏发电系统建模及其参数辨识技术研究[D]. 合肥: 合肥工业大学, 2018.
(  0) 0)
|
| [10] |
靳伟佳. 光伏并网逆变器动态模型及其参数辨识研究[D]. 北京: 华北电力大学, 2018.
(  0) 0)
|
| [11] |
何昊, 崔成, 贾希浩, 等. 基于暂态响应轨迹的光伏逆变器参数辨识方法[J].
智慧电力, 2022, 50(4): 51-58 HE Hao, CUI Cheng, JIA Xihao, et al. Photovoltaic Inverter Parameter Identification Method Based on Transient Response Trajectory[J]. Smart Power, 2022, 50(4): 51-58 (  0) 0)
|
| [12] |
张成, 赵涛, 朱爱华, 等. 弱电网下并联逆变器稳定性及电、能质量治理研究[J].
电力工程技术, 2022, 41(3): 224-230 ZHANG Cheng, ZHAO Tao, ZHU Aihua, et al. Stability and power quality control of parallel inverters in weak current network[J]. Electric Power Engineering Technology, 2022, 41(3): 224-230 (  0) 0)
|
| [13] |
梁亦峰. 基于逆变器的虚拟同步发电机控制建模与仿真[J].
机电工程技术, 2021, 50(3): 93-96 LIANG Yifeng. Modeling and Simulation of Virtual Synchronous Generator Based on Inverter Control[J]. Mechanical & Electrical Engineering Technology, 2021, 50(3): 93-96 DOI:10.3969/j.issn.1009-9492.2021.03.021 (  0) 0)
|
| [14] |
高菲菲, 杨俊友, 董鹤楠, 等. 基于虚拟同步发电机的光伏逆变器电压暂降自适应补偿控制策略[J].
东北电力技术, 2020, 41(6): 5-10 GAO Feifei, YANG Junyou, DONG Henan, et al. Strategy of PV Inverter Voltage Sag Adaptive Compensation Control Based on Virtual Synchronous Generator[J]. Northeast Electric Power Technology, 2020, 41(6): 5-10 DOI:10.3969/j.issn.1004-7913.2020.06.002 (  0) 0)
|
| [15] |
郑伟强, 高长伟, 郑炜亮, 等. 一种改进的光伏并网逆变器双闭环控制策略[J].
可再生能源, 2022, 40(2): 260-265 ZHENG Weiqiang, GAO Changwei, ZHENG Weiliang, et al. An improved double closed loop control strategy for photovoltaic grid-connected inverter[J]. Renewable Energy Resources, 2022, 40(2): 260-265 (  0) 0)
|
| [16] |
张明冉, 常治国, 吴昊, 等. 一种新型光伏控制器MPPT控制策略[J].
电力电子技术, 2021, 55(9): 75-77 ZHANG mingran, CHANG Zhiguo, WU Hao, et al. A New Control Strategy for MPPT Photovoltaic Controller[J]. Power Electronics, 2021, 55(9): 75-77 DOI:10.3969/j.issn.1000-100X.2021.09.019 (  0) 0)
|
| [17] |
牛秋实, 施建强, 惠子轩. 基于改进型双模糊控制的光伏MPPT的研究[J].
电源技术, 2021, 45(6): 781-785 NIU Qiushi, SHI Jianqiang, HUI Zixuan. Research on photovoltaic MPPT based on improved double fuzzy control[J]. Chinese Journal of Power Sources, 2021, 45(6): 781-785 (  0) 0)
|
| [18] |
王仁明, 胡梦帆, 张赟宁. 基于滑模控制方法的光伏系统MPPT策略[J].
电源技术, 2021, 45(4): 478-481 WANG Renming, HU Mengfan, ZHANG Yunning. MPPT strategy for photovoltatic system based on sliding mode control method[J]. Chinese Journal of Power Sources, 2021, 45(4): 478-481 DOI:10.3969/j.issn.1002-087X.2021.04.014 (  0) 0)
|
| [19] |
孙恺, 刘光宇. 基于改进PSO算法的光伏发电系统MPPT控制策略[J].
传感器与微系统, 2021, 40(1): 49-52 SUN Kai, LIU Guangyu. MPPT control strategy for PV generation system based on improved PSO algorithm[J]. Transducer and Microsystem Technologies, 2021, 40(1): 49-52 (  0) 0)
|
| [20] |
中国电力企业联合会. 光伏发电系统模型及参数测试规程: GB/T 32892-2016[S]. 北京: 中国标准出版社, 2016.
(  0) 0)
|
| [21] |
韩平平, 范桂军, 孙维真, 等. 基于数据测试和粒子群优化算法的光伏逆变器LVRT特性辨识[J].
电力自动化设备, 2020, 40(2): 4954-54 HAN Pingping, FAN Guijun, SUN Weizhen, et al. Identification of LVRT characteristics of photovoltaic inverters based on data testing and PSO algorithm[J]. Electric Power Automation Equipment, 2020, 40(2): 4954-54 (  0) 0)
|
| [22] |
刘晓丹. 基于粒子群算法的光伏系统最大功率点跟踪研究[D]. 南京: 南京邮电大学, 2013.
(  0) 0)
|
| [23] |
孙黎霞, 林雪, 金宇清, 等. 基于粒子群优化算法的并网光伏发电单元建模[J].
电网技术, 2015, 39(5): 1213-1218 SUN Lixia, LIN Xue, JIN Yuqing, et al. Modeling of Grid-Connected Photovoltaic Generation Unit Based on Particle Swarm Optimization Algorithm[J]. Power System Technology, 2015, 39(5): 1213-1218 (  0) 0)
|
 2022, Vol. 40
2022, Vol. 40