2. 浙江运达风电股份有限公司内蒙古分公司, 呼和浩特 010020;
3. 内蒙古电力(集团)有限责任公司薛家湾供电分公司, 内蒙古 鄂尔多斯 010300;
4. 西安工程大学 机电工程学院, 西安 710071
2. Zhejiang Windey Co., Ltd., Inner Mongolia Branch, Hohhot 010020, China;
3. Inner Mongolia Power Group Co., Ltd., Xuejiawan Power Bureau Supply Company, Ordos 010300, China;
4. School of Mechanical and Electrical Engineering, Xi'an Polytechnic University, Xi'an 710071, China
配电台区电压质量是衡量配电台区运行水平的重要指标。但仅依靠电压均方根值,无法获得电压质量的综合评价,应结合负荷水平、台区自身及上级供电情况综合考虑。目前配电台区电压质量评价研究开展较少,但智能化的评估方法已广泛应用于电力[1-11]、公共交通[12]、资源[13]及环境[14]等领域。智能化评估的主要步骤包括指标赋权及量化评分两步。根据原理差异,赋权法可分为主观赋权及客观赋权。常用的主观赋权法包括层次分析法(Analytic Hierachy Procass,AHP)[4]及环比评分法[5],主要基于专业知识或专家经验,并通过一致性校验提升结果的客观性,但主观法无法利用样本自身的信息量。常用的客观赋权法有熵权法[6-8]及CRITIC法[9]。这些方法不受专家主观因素影响,基于信息熵(Entropy)的概念,确定指标权重。实际应用中通常将主客观权重优化组合,得到综合权重。实践中可选取博弈论[10]、最小二乘法[11]、最小信息增益[12]等模型计算综合权重。量化评分通常依据指标权重确定对象的得分,常用方法有理想解贴近度排序法(Technique for Order Preference by Similarity to an Ideal Slution,TOPSIS)[13]、灰色关联度法[14]、模糊评价法[15]以及VIKOR法[16]等。
对于配电台低电压质量的智能化评估,文献[1] 建立了一套包括配电设备、线路、无功补偿及电网结构等准则的低压配电网评价体系,并利用层次分析法开展低压配电网的综合评估。文献[2]建立了针对农村配电网的能效评价体系,将主成分分析法与层次分析法有机结合,用于能效评估。文献[3]提出一种基于配电台区负荷预测,估算线路末端电压跌落的电压越限风险评估方法。
本文综合考虑配电设备、低压运行、中压网架、中压运行等因素,建立了包含“4类12指标”的评价体系。并利用AHP及熵权法分别获取主、客观权重,利用最小信息增益原理确定综合权重,旨在找出一种配电台区电压质量精准评估方法,从而为精准识别电压异常的配电台区提供技术支持。
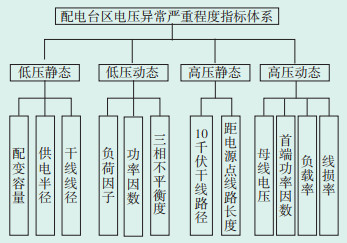
1 配电台区电压质量指标评价体系首先考虑配电台区自身因素(低压)对配电台区电压质量的影响。基于二端点配电模型进行理论分析可知,配变容量低、台区干线线径细、供电半径过长、配变重过载、三相负荷不平衡、功率因数低均可导致电压越限。其中配电容量、干线线径、供电半径为台区静态指标,反映台区的设计水平。配变负载率、三相负荷不平衡度及功率因数为动态指标,反映台区的实际运行水平。台区高压侧如果存在电压异常也会对台区电压产生影响。高压影响因素主要因素主要包括10 kV干线线径、台区距离电源点10 kV线路长度、线路首端功率因数、线损率、负载率及母线电压等。将上述指标按照静态及动态进行区分,最终得到配电台区电压指标体系,如图 1所示。
|
| 图 1 配电台区电压质量评价指标体系 Figure 1 Voltage quality evaluation index system of distribution station area |
建成配电台区电压质量评价指标体系后,需确定各指标权重。利用AHP法确定主观权重,主要步骤如下。
(1)步骤1,建立比较矩阵X。比较矩阵的各元素可反映两指标间的相对重要程度,以xij为例,其值反映了指标i相对于指标j的重要程度。
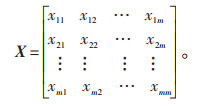
|
(1) |
需要说明,各元素满足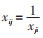
(2)步骤2,一致性校验。由于评估专家的认知差异以及计算错误等因素,比较矩阵可能违背重要度传递性原则。如xij > 1且xjk > 1,而xijkj < 1。故对比较矩阵进行一致性校验。根据文献[11],分别定义一致性指数CI及一致性因子CR如下:
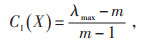
|
(2) |
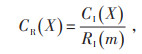
|
(3) |
式中:λmax为比较矩阵的最大特征根,m为矩阵阶数;RI为随机一致性系数。当一致性因子小于0.1,则认为比较矩阵有效。为了避免因未通过一致性测试导致重复打分,此处进行改进。首先对各指标分别进行排序,假设共有m个指标,则重要度最高的指标重要度得分为m,按照重要度顺序,得分依次递减,重要度最低的指标得分为1。各评分结果具有同等权重,统计各指标平均得分,进而确定指标重要度顺序。从而建立专家共识机制。只要专家评分不违背指标权重的共识,即可满足一致性要求。
(3)步骤3,计算指标权重。确定指标权重的方法主要有特征向量法、列向量求和法以及几何平均距离法[14],其中特征向量法最为常用。对于指标i的权重ωi,基于特征向量的权重计算公式见公式(4):
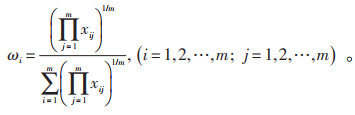
|
(4) |
熵权法是常用的客观赋权法,该方法属于间接赋权法,根据样本中列向量,计算指标的信息熵,间接确定指标权重。信息熵值越大,指标权重越高,反之亦然。熵权法主要步骤如下。
(1)步骤1,构建初始比较矩阵Y。若指标数及评价对象数分别为m和n,其初始评价矩阵为m×n矩阵,元素yij为对象i的第j个指标值,决策矩阵的形式如下:
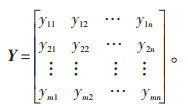
|
(5) |
(2)步骤2,无量纲化处理。考虑各指标单位不同,所得熵值不具备可比性。故对初始比较矩阵进行无量纲化及归一化处理。对Y中任意元素yij进行归一化,得到归一化的比较矩阵P,则P中元素Pij计算公式如下:
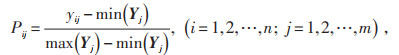
|
(6) |
式中:Yj为矩阵第j列构成的列向量;max(Yj),min(Yj) 分别为第j列元素的最大、最小值。
(3)步骤3,计算各指标权重。首先计算各指标熵值,根据熵值确定权重,公式如下:
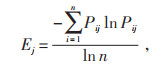
|
(7) |
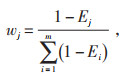
|
(8) |
式中:Ej为第j列的信息熵;wj为第j列对应指标的权重。需要指出,由于熵权法过于依赖数据质量,某指标数值波动幅度越小,其权值越小,无法反映真实权重,故在实际中,可能需要对原始数据加以处理,适当增大指标熵值。
2.3 基于最小信息熵增确定综合权重在2.1、2.2节分别得到指标的主观及客观权重后,同时也指出两种权重均存在一定的缺陷。因而需要采用某种模型,计算综合权重。无论采用何种权重计算模型,所得的综合权重在信息量上均与原有的权重存在差异,即信息熵增。因而以综合权重与上述两种权重信息熵增之和最小,即最小信息熵增,建立权重计算模型:
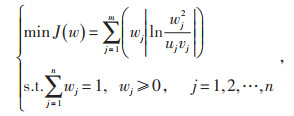
|
(9) |
式中:uj,vj,wj分别为指标j的主观、客观、综合权重;n为指标总数。
根据文献[6]得到权重计算公式:
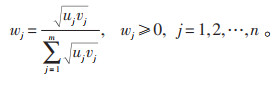
|
(10) |
TOPSIS法最早由文献[16]提出。其核心思想是建立在“距离”概念之上。首先通过样本构建极优向量和极差向量,各对象与极优向量距离越近,与极差向量距离越远,则获得评价分数越高。传统TOPSIS法主要步骤如下。
(1)步骤1,构建初始矩阵。初始矩阵与熵权法中评价矩阵Y的构建方法完全一致,此处省略;
(2)步骤2,构建加权矩阵。对步骤1的初始矩阵各元素yij,利用式(11)计算其加权值eij,从而得到加权矩阵E:

|
(11) |
(3)步骤3,利用式(12)从加权评价矩阵E获取极值向量。
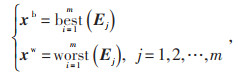
|
(12) |
其中,xb、xw为极优、极差向量;best(Ej) 为矩阵E第j列最优值,worst(Ej) 为最差值。从式(13)可以看出,由加权矩阵的全部列向量的极优值构成极优向量,由全部列向量的极差值构成极差向量。但上述方法所得极值向量的质量很大程度依赖待加权矩阵的分散程度。考虑极端的情形,如果加权矩阵全部元素均靠近极优值或极差值分布,导致极向量和极差向量非常接近,则TOPSIS法的评价效果将严重劣化。可以说,对象取值越分散,对象集规模越大,极值向量质量越高,越具有代表性。因而对传统TOPSIS方法加以改进,引入参考样本集,样本集由较优和较差的典型数据项构成,然后通过K-Means聚类确定极值向量,主要流程如图 2所示。
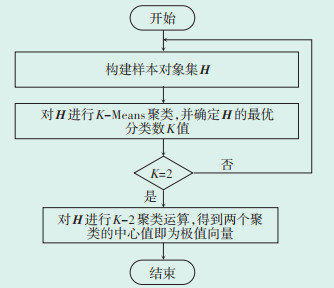
|
| 图 2 基于K-Means聚类的极值向量确定方法 Figure 2 Extreme value vector determination method based on K-Means clustering |
首先构建参考样本集H,样本集中较优及较差对象数量基本一致。然后对H进行K-Means聚类,并确定最优分类数K。如果K=2,说明参考样本集主要包含两类数据满足要求,则两个聚类的中心即可作为极值向量,否则,重新构建参考样本集。步骤2中确定最优K值的常用方法包括肘标准法(Elbow)、平均轮廓系数法(MSC,Mean Silhouette Coefficient)[17]。Elbow法只在聚类误差曲线满足手肘形状的前提下适用,故使用平均轮廓系数法确定最优K值。
(4)步骤4,计算对象集中各对象与极值向量的欧氏距离。

|
(14) |
其中,dib、diw分别为对象i与极值向量的欧式距离,xjb 、xjw 为极优、极差向量第j维分量。定义对象i的贴近度Si如下:
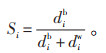
|
(15) |
贴近度反映了对象与极优向量的靠近度和极差相量的远离度,可将贴近度视为对象的评价得分,对象与极优相量距离越近,与极差相量距离越远,其得分越高。
3.2 配电台区电压异常综合评价方法综合上述方法及理论,最终确定配电台区电压异常严重度综合评价方法,其流程如图 3所示。
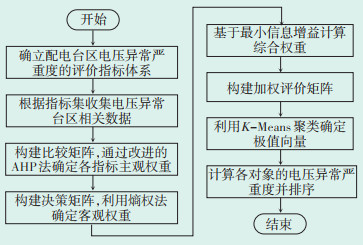
|
| 图 3 基于TOPSIS的配电台区电压质量评价方法 Figure 3 Voltage quality evaluation method of distribution station area based on TOPSIS |
以北方某市农村电网的电压异常台区为测试对象,测试配电台区电压质量评价算法。由于近年来农村负荷快速增长,农网改造工程相对滞后,导致该市农村低电压投诉率逐年增多。通过供电电压监测系统、投诉情况等途径累计收集近3年低电压台区累计2502个。
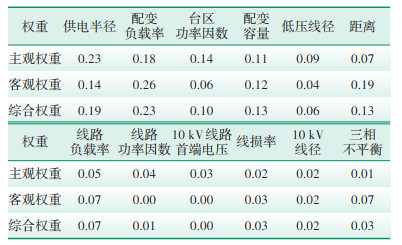
4.2 指标权重确定利用2.1节及2.2节方法分别计算主、客观权重。再利用2.3节最小信息熵增法计算综合权重。得到三类权重结果如表 1所示,其指标主观权重从左到右依次降低。
| 表 1 配电台区电压质量指标权重 Table 1 Weight of voltage quality indicators in the distribution station area |
构建参考样本集,确定极值向量,分别利用改进TOPSIS及传统TOPSIS计算严重度,比较两种方法的优劣,并对严重度评估结果加以分析。
4.3.1 样本训练集测试分别选取100个优质电压台区及100个低电压台区,组成样本集。K值范围选取从2至9,绘制平均轮廓系数曲线如图 4所示。
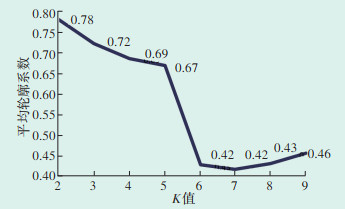
|
| 图 4 K-平均轮廓系数曲线 Figure 4 K-average contour coefficient curve |
从图中可以看出,当分组数为2,平均轮廓系数有最大值0.78,说明样本集最优分类数K值为2,故可作为参考样本集,以两个聚类的中心点作为极值相量。分别采用传统TOPSIS法及改进的TOPSIS法对样本集进行电压质量评估,所得评价结果如图 5所示。可以看出,传统TOPSIS模型将样本集中台区划分至(0,0.3),(0.3,0.5),(0.5,1.0)3个区间。各区间所含台区数量分别为105、66、29。而使用本文改进的TOPSIS模型,样本台区全部落入(0,0.3),(0.5,1.0)两个区间,两个区间所含台区数量均为100。比较改进后的TOPSIS法,传统TOPSIS法存在10个台区的错误分类,准确率为95%,而改进后的TOPSIS法分类准确率则为100%。由此可以得出,利用改进的TOPSIS模型可获得更高的评价及分类准确度。
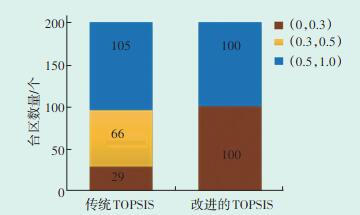
|
| 图 5 两种TOPSIS模型针对样本测试集的电压质量评价结果 Figure 5 Voltage quality evaluation results of two TOPSIS models for sample test sets |
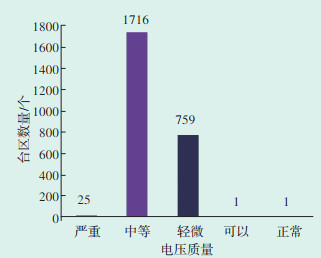
利用改进TOPSIS模型,评估2502个台区的电压质量。将(0,0.3),(0.3,0.5),(0.5,1.0)分别定义为电压质量异常、可疑及正常电压质量区间。将问题区间进一步细分为轻微异常、中等异常及严重异常,对应区间定义为(0,0.1),(0.1,0.2),(0.2,0.3)。配电台区电压质量评估结果分布如图 6所示,可见几乎全部台区均为电压异常台区,严重、中等、轻微异常台区数量分别有25、1716、759个。由于所收集台区主要为存在电压异常问题的台区,故进一步验证了本文方法的准确性。
|
| 图 6 配电台区电压质量评估结果分布 Figure 6 Distribution of voltage quality assessment results in the distribution station area |
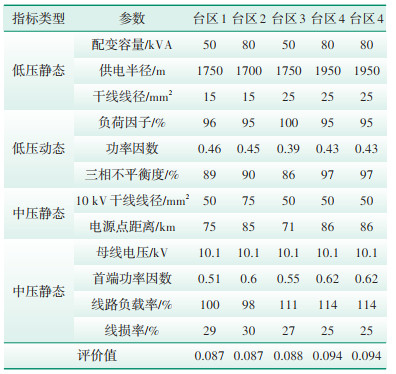
从2502个台区的评价结果中,选取评价值最低的5个台区,台区参数见表 2。
| 表 2 得分最低的5个低电压台区 Table 2 The five low⁃voltage stations with the lowest scores |
表 2中台区低压参数均存在供电半径长、线径细、重载、严重三相不平衡(不平衡度高于80%)等问题;10 kV方面,台区全部处于配电线路末端(距离电源点71~85 km)、线径细(50 mm2或75 mm2)、线损率高(高于25%)、重载、无功支撑不足(功率因数0.51~0.62)。上述台区参数均严重偏离文献[18]推荐数值,进一步验证了本文算法的有效性。在配电台区改造时,建议将上述台区优先列入改造计划。
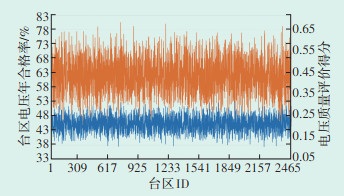
4.3.2.3 测试3为了进一步验证本文电压质量评价算法,通过省网公司供电电压监测系统导出台区样本的年度电压合格率。若台区电压质量评价趋势与电压合格率趋势一致,则可证明该评价算法的有效性。样本台区电压质量评价得分及年度合格率如图 7所示。从中可以看出,二者变化趋势基本一致。
|
图 7 配电台区样本年电压合格率与电压质量评价得分对比
Figure 7 Comparison of annual voltage qualification rate and voltage quality evaluation score of distribution station area samples
图中: —年度电压合格率; —年度电压合格率; —电压质量评价得分。 —电压质量评价得分。
|
本文提出了一种针对配电台区电压质量的评估方法,具体如下。
(1)为精确评价配电台区电压质量,建立4类12指标的配电台区电压指标评价指标体系。指标体系覆盖了配电台区高压侧及低压侧与电压相关的主要动态参数及静态参数。
(2)改进AHP法,基于专家共识构建有序比较矩阵,确保评价结果满足一致性要求。
(3)改进TOPSIS评估模型,引入样本对象集,基于K-Means聚类法确定极值相量,将台区分类的准确率从95%提升至100%,可有效提升极值相量的典型性;利用样本测试集对改进TOPSIS模型及传统模型进行对比测试,结果表明,改进TOPSIS方法可获得更高的评价准确度。
(4)利用本文TOPSIS模型,评估2502个配电台区的电压质量。结果表明,绝大部分台区为电压异常台区,与实际情况相符。另外,分析评价值最低的5个台区,其参数严重偏离合理区间,间接证明本文TOPSIS模型的有效性。后续将利用规模更大的测试样本,对模型进行完善。
| [1] |
李峰, 孙波, 王轩, 等. 层次分析法结合熵权法评估农村屋顶光伏系统电能质量[J].
农业工程学报, 2019, 35(11): 159-166 LI Feng, SUN Bo, WANG Xuan, et al. Power quality assessment for rural rooftop photovoltaic access system based on ana-lytic hierarchy process and entropy weight method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(11): 159-166 (  0) 0)
|
| [2] |
韩晓慧, 杜松怀, 苏娟, 等. 基于组合赋权法的农村低压配电网能效综合评价方法[J].
农业工程学报, 2014(16): 195-202 HAN Xiaohui, DU Songhuai, SU Juan, et al. Energy efficiency evaluation method of rural low-voltage distribution network based on combination weight method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014(16): 195-202 (  0) 0)
|
| [3] |
苏海林, 龙翩翩. 基于负荷预测的0.4 kV配网低电压风险评估方法[J].
电力信息与通信技术, 2020(3): 53-58 SU Hailin, LONG Pianpian. A Low Voltage Risk Assessment Method of 0.4 kV Distribution Network Based on Load Forecasting[J]. Electric Power Information and Communication Technology, 2020(3): 53-58 (  0) 0)
|
| [4] |
刘亚丽, 王旭东, 赵迎春, 等. 基于TOPSIS法的充电机运行性能组合赋权评价方法[J].
电力工程技术, 2019, 38(5): 130-137 LIU Yali, WANG Xudong, ZHAO Yingchun, et al. Evaluation-method for the combination weighting of charing machine operating performance based on TOPSIS method[J]. Jiangsu Electrical Engineering, 2019, 38(5): 130-137 (  0) 0)
|
| [5] |
卫泽晨, 赵凤展, 王佳慧, 等. 网格化中低压智能配电网评价指标体系与方法[J].
电网技术, 2016, 40(1): 249-255 WEI Zechen, ZHAO Fengzhan, WANG Jiahui, et al. Gridding Evaluation Index System and Method of MV and LV Intelligent Distribution Network[J]. Power System Technology, 2016, 40(1): 249-255 (  0) 0)
|
| [6] |
赵书强, 汤善发. 基于改进层次分析法、CRITIC法与逼近理想解排序法的输电网规划方案综合评价[J].
电力自动化设备, 2019, 39(3)143-148, 162 ZHAO Shuqiang, TANG Shanfa. Comprehensive evaluation of transmission network planning scheme based on improved analytic hierarchy process, CRITIC method and TOPSIS[J]. Electric Power Automation Equipment, 2019, 39(3)143-148, 162 (  0) 0)
|
| [7] |
杨月新, 车延博, 杨立勋. 电动汽车充电机运行状态多指标综合评估[J].
电力自动化设备, 2018, 38(3): 72-79 YANG Yuexin, CHE Yanbo, YANG Lixun. Multi-index comprehensive evaluation of running state for electric vehicle charger[J]. Electric Power Automation Equipment, 2018, 38(3): 72-79 (  0) 0)
|
| [8] |
吴昊, 朱自伟. 基于熵权-层次分析法综合指标的电网关键节点辨识[J].
电测与仪表, 2020, 57(24): 93-100 WU Hao, ZHU Ziwei. Key nodes identification in power grid based on comprehensive index calculated by the entropy weight -analytical hierarchy process[J]. Electrical Measurement And Instrumentation, 2020, 57(24): 93-100 (  0) 0)
|
| [9] |
南琦琦, 穆云飞, 董晓红, 等. 电动汽车快速充电网综合评估指标体系与方法[J].
电力系统自动化, 2020, 44(1): 83-91 NAN Qiqi, MU Yunfei, DONG Xiaohong, et al. Comprehensive Evaluation Index System and Method for Fast Charging Network of Electric Vehicles[J]. Automation of Electric Power Systems, 2020, 44(1): 83-91 (  0) 0)
|
| [10] |
杨国生, 戴飞扬, 王文焕, 等. 基于灰度关联法和TOPSIS法的继电保护状态评估综合算法研究与应用[J].
中国电力, 2019, 52(2): 94-103 YANG Guosheng, DAI Feiyang, WANG Wenhuan, et al. Research and Application of Comprehensive Algorithm of Relay Protection Status Assessment Based on Gray Correlation Analysis and TOPSIS Method[J]. Electric Power, 2019, 52(2): 94-103 (  0) 0)
|
| [11] |
Bartlomeijczyk M, Gutten M, Hamacek S. A combined TOPSIS and FA based strategic analysis of technical condition of high power transformers[J].
Advances in Electrical and Electronic Engineering, 2013, 11(4): 152-160 (  0) 0)
|
| [12] |
WEN Huiying, WU Lufan, MEI Jiajun. Fuzzy comprehensive evaluation of Guangzhou-Foshan public transit satisfaction of inter-city based on improved AHP method[J].
Journal of Sun Yatsen University(Natural Science Edition), 2018, 57(5): 64-71 (  0) 0)
|
| [13] |
Zardari N, Ahmed K, Shirazi S, et al.
Weighting methods and their effects on multi-criteria decision making model outcomes in water resources management[M]. Cham: Springer International Publishing, 2015: 45-67.
(  0) 0)
|
| [14] |
LIU Dahai, GONG Wei, XING Wenxiu, et al. Comprehensive method for determining the weights of vulnerability assessment indexes on islands and the coastal zone based on the AHP weight method and entropy weight method[J].
Chinese Journal of Marine Environmental Science, 2015, 34(3): 462-467 (  0) 0)
|
| [15] |
Papathanasiou J, Ploskas N.
Multiple criteria decision aid methods, examples and python implementations[M]. Cham: Springer Optimization and Its Applications, 2018: 42-67.
(  0) 0)
|
| [16] |
宋新甫, 徐龙秀, 张艳, 等. 结合灰色关联分析的熵权VIKOR法输电网规划方案综合评价方法[J].
电工技术, 2019(11): 11-14 SONG Xinfu, XU Longxiu, ZHANG Yan, et al. Comprehensive Evaluation Method of Transmission Network Planning Scheme Based on Entropy Weight VIKOR Method Combined with Grey Relational Analysis[J]. Electric Engineering, 2019(11): 11-14 (  0) 0)
|
| [17] |
Joaquín P, Almanza O, Vega V, et al.
The K-Means algorithm evolution, introduction to data science and machine learning[M]. March: Intech Open, 2020: 1-22.
(  0) 0)
|
| [18] |
国家电网公司. 配电网技术导则: Q/GDW 10370—2016[S]. 北京: 中国电力出版社, 2016.
(  0) 0)
|
 2023, Vol. 41
2023, Vol. 41