2. 内蒙古电力经济技术研究院, 呼和浩特 010010
2. Inner Mongolia Power Economy and Technology Research Institute, Hohhot 010010, China
当前,存量配电网面临的挑战主要有容量扩展、可靠性提升、电能质量提升等,而传统解决方案存在配电网改造复杂、容量提升有限等问题。利用柔性直流技术对配电网进行升级改造,可实现配电系统异源合环运行。文献[1-4]研究了基于智能软开关(Soft Normally Open Point,SNOP)的配电网运行优化方法,并将其和传统的配电网络重构进行了对比,从降低有功网损、应对分布式电源与负荷实时波动、改善电压水平等方面验证了SNOP的优势。文献[5-6]研究了利用SNOP提高有源配电网中的光伏渗透率,并提出1种具有工程价值的运行优化控制策略。文献[7-9]对含SNOP的配电网相关技术进行了研讨,并对其发展趋势进行了展望。文献[10]介绍了世界首个将多端SNOP装置应用于配电网柔性闭环运行的工程——北京八达岭经济开发区多端柔性闭环配电网示范工程。
在配电网联络开关处接入SNOP构成的柔性配电网,改变了存量配电网辐射状的供电模式,可在线路/设备检修或故障情况下,快速转移负荷,提供紧急功率支援,从而提高配电网的可靠性。本文以SNOP为研究对象,分析其在坐标系中的数学模型,建立双闭环控制系统,在此基础上对SNOP进行仿真分析,分析其动态工作特性与暂态响应特性,以验证SNOP控制系统的可行性。
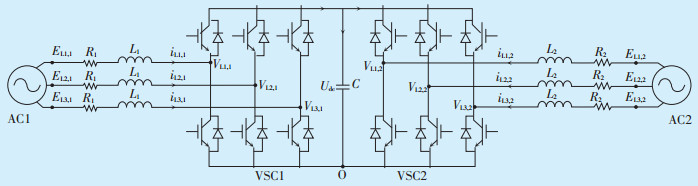
1 SNOP数学模型与控制系统 1.1 SNOP在同步旋转坐标系下的数学模型SNOP的功能是基于对全控型电力电子器件的控制而实现的,其具体装置应用目前主要有3种[4]:电压源型变流器(Voltage Source Converter,VSC)、统一潮流控制器(Unified Power Flow Controller,UPFC)和静止同步串联补偿器(Static Synchronous Series Compensator,SSSC),本文以背靠背VSC为研究目标,其系统结构如图 1所示。SNOP由2个背靠背VSC构成,中间直流侧通过电容器并联。相电抗器L1和L2与交流侧进行功率传递,同时滤除VSC输出谐波;电容C为直流侧提供电压支撑并滤除谐波。
|
图中:L1,L2—相电抗器;EL1,2,EL2,2,EL3,2—交流系统2的三相电压;R1,R2—相电抗器与线路损耗的等效电阻;EL1,1,EL2,1,EL3,1—交流 系统 1的三相电压;VL1,1,VL2,1,VL3,1—VSC1交流侧的三相电压;C—电容;VL1,2,VL2,2,VL3,2—VSC2交流侧的三相电压。 图 1 SNOP系统结构示意图 |
三相静止abc坐标系下的SNOP数学模型的物理意义明确,但VSC交流侧的电气量均为时变量,给控制系统的设计带来不便。PARK变换[11]可将三相静止坐标系变换为与系统基波频率同步旋转的dq坐标系,时变交流量可转变为直流量。坐标系下的d、q坐标轴相互垂直,d、q轴分量实现了解耦,从而可简化控制系统的设计,同时可选择交流系统电压矢量与同步旋转dq坐标系中的d轴重合,即d轴按照交流系统电压矢量定向。可推导SNOP系统在同步旋转dq坐标系中的数学模型[12]为:
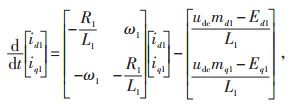
|
(1) |
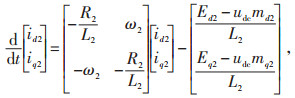
|
(2) |
式中udc —直流侧电容电压;
ω1、ω2 —交流系统相电压的角频率;
id1、id2 —VSC交流侧输出的电流矢量的d轴分量;
iq1、iq2 —VSC交流侧输出的电流矢量的q轴分量;
Ed1、Ed2 —交流系统电压矢量的d轴分量;
Eq1、Eq2 —交流系统电压矢量的q轴分量;
md1、md2 —VSC调制开关函数的d轴分量;
mq1、mq2 —VSC调制开关函数的q轴分量。
系统运行在稳定状态时,直流侧电容电压的方程为:
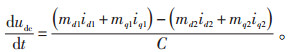
|
(3) |
由式(1)、(2)可以得知,SNOP的数学模型为d、q轴互相耦合的非线性系统。其中,[id1 iq1 id2 iq2 udc]T为状态变量,[md1 mq1 md2 mq2]T为控制变量,交流系统电压Ed、Eq一般为已知量,设定控制变量后,即可确定状态变量的值。
在三相对称交流系统中,如果仅考虑基波分量,则模型中d、q轴分量在稳态时均为直流分量,有功分量用d轴分量表示,无功分量用q轴分量表示,从而有利于独立控制有功分量和无功分量。对于背靠背VSC组成的SNOP耦合系统,控制器设计可以采用PI控制器实现解耦控制。
忽略线路和VSC元件的功率损耗,SNOP两侧VSC1和VSC2的有功功率Pj和无功功率Qj输出方程[11]可表示为:
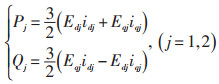
|
(4) |
系统不同的控制目标有不同的控制策略,SNOP连接交流系统时的控制目标是有功功率与无功功率的独立控制。目前工程上通用的控制方法是直接电流控制,即矢量控制,通常由功率外环和电流内环2个控制环构成,具有快速的电流响应特性,且内在限流能力较好。电流内环控制器完成VSC交流侧电流相位和波形的直接控制,以便快速追踪目标参考电流值。外环功率控制器根据控制目标实现定有功功率控制、定无功功率控制、定直流电压控制等[13]。
1.2.1 电流内环控制电流内环的控制策略响应能力较快,且没有稳态误差,SNOP系统中2个VSC均采用双闭环控制。由式(1)、(2)可以看出,SNOP中d、q轴电流之间存在耦合,仅依靠电流反馈控制来消除耦合并不可行,因此需要对id和iq进行解耦。
以图(1)中的VSC1为例,影响d、q轴电流的因素有:控制量md1udc、mq1udc,电压耦合分量ω1L1id1、ω1L1iq1及电网电压Ed1和Eq1。为消除电网电压波动和电流耦合带来的影响,可在式(1)与(2)中引入电网电压Ed1和Eq1及VSC1交流侧d、q轴电流分量,组成的控制量可用以消除这些耦合分量,从而完成id和iq的解耦控制。在控制量中引入的电压前馈补偿和电流反馈如下[11]:
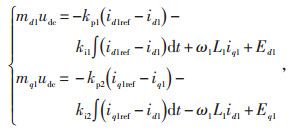
|
(5) |
式中id1ref、iq1ref —通过外环控制器得到的内环d、q轴电流测量信号的参考值;
kp1、kp2、ki1、ki2 —PI控制器参数。
PI控制器的作用是使VSC输出电流准确跟踪目标电流参考值。将式(5)带入式(1)、(2)可得:
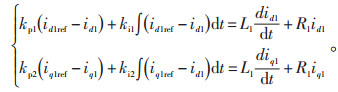
|
(6) |
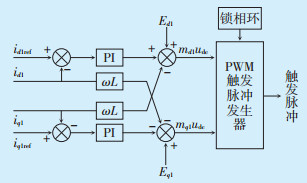
由式(6)可知,引入电流反馈可对id、iq进行独立控制,电压前馈补偿的引入可进一步提高系统的动态特性。电流内环控制原理如图 2所示。
|
图 2 电流内环控制原理 |
为了保持SNOP的有功平衡和直流电压稳定,背靠背VSC中有1个必须采用定直流电压控制,而另1个可以采用定有功功率控制或定频率控制。
(1)定直流电压控制
在忽略R1、R2和VSC损耗时,变流器交直流两侧的有功功率Pac、Pdc维持平衡,即:
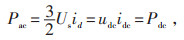
|
(7) |
式中Us —系统电压的模值。
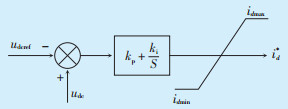
当有功功率经过VSC两侧出现不均衡时,会造成直流电压振动,功率不平衡产生的能量偏差使电容充放电,直至电容电压稳定。故VSC采用定直流电压控制方式,等同于1个平衡有功功率的节点[13]。定直流电压控制原理如图 3所示。
|
图中:udcref—udc参考值;idmax、idmin—id的最大值和最小值;id* —内环d轴电流信号指令值。 图 3 定直流电压控制原理 |
(2)定功率控制
当系统电压运行稳定时,d轴方向选为系统电压Us的方向,即有Ed = Us,Eq = 0,因此SNOP系统功率输出方程为:
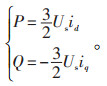
|
(8) |
可以通过id和iq分别对P和Q进行控制,从而实现有功功率和无功功率的独立调整。有功功率和无功功率控制器的设计可采用稳态逆模型[4]。据式(8)可得出有功电流和无功电流的预估值i′d、i′q:
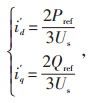
|
(9) |
式中Pref —有功功率参考值;
Qref —无功功率参考值。
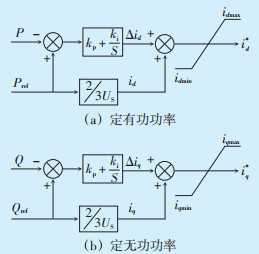
利用PI控制器可消除静态误差。外环定功率控制原理如图 4所示。
|
图中:iq*—内环q轴电流信号指令值。 图 4 外环定功率控制原理 |
在PDACD/EMTDC环境下对图 1所示模型进行电磁暂态仿真,研究SNOP系统的动态工作特性与暂态响应特性。设定系统处于三相平衡状态,仿真模型参数设置如下:交流系统电压10 kV,电容C=5 mF,开关频率6400 Hz,直流电容电压30 kV,相电抗器电抗0.02 H,忽略等效损耗电阻R1、R2,调制方式采用SPWM,仿真步长为0.000 01 s。
2.1 SNOP动态工作特性阶跃响应能够很好地反映控制器的暂态调控特性,仿真中设置有功功率参考指令以额定值反向传输,可更好地检验SNOP的抗负载扰动能力。
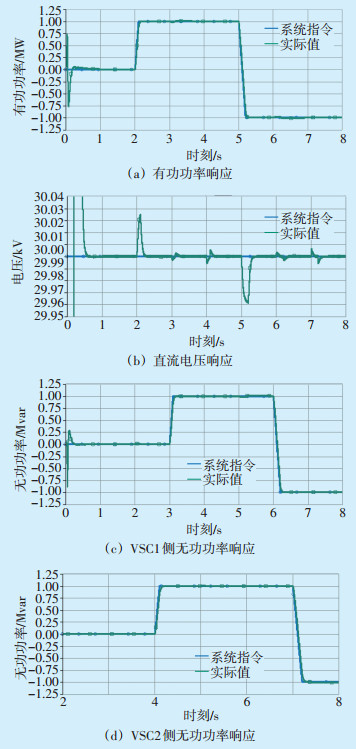
SNOP系统的动态工作特性如图 5所示。由图 5可知,SNOP动态工作特性良好,能够准确、快速地跟踪系统参考指令值。在第5 s时,有功功率传输从1 MW变为-1 MW,直流侧电容电压的波动仅为0.04 kV,但有功功率响应时间约为230 ms,时间较长,可解释为通过降低有功调节速率,从而减少直流电压的波动。SNOP在有功功率传输过程中,直流电压出现2次较大波动,这是因为SNOP在调节有功功率时,其两侧出现的功率瞬时不平衡,一般可通过降低有功功率调节速率或增大电容容量来减少直流电压波动。在直流电压出现2次较大扰动时,造成两侧无功功率调节出现小波动,而两侧无功功率的阶跃突变对直流电压的影响很小[11]。
|
图 5 SNOP系统动态工作响应 |
综上所述,SNOP在功率传输过程中,有功突变会引起直流电容电压的较大波动,而SNOP两侧无功功率的突变对直流侧电容电压波动的影响很小。即有功功率、无功功率的传输实现了独立控制,验证了基于直接电流控制的双闭环协调控制器的可行性。
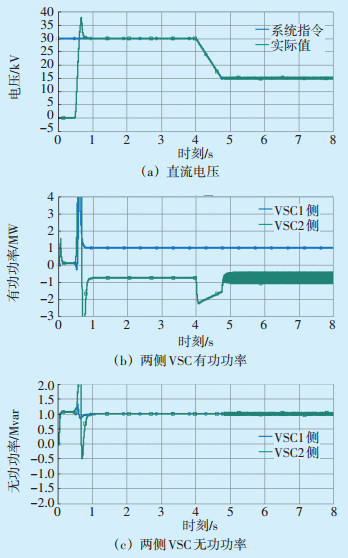
2.2 SNOP暂态响应特性 2.2.1 直流电压阶跃变化仿真设定在第4 s时,直流电压指令值突变为15 kV,观察各项测量值的变化,仿真结果见图 6。
|
图 6 直流电压阶跃变化仿真 |
由图 6可知,直流电压测量值能准确跟踪变化,直流电压的降低除了使VSC2侧的有功功率产生波动外,对VSC1侧的有功功率、两侧VSC的无功功率均没有影响;但同时会导致直流电流增大,以保持有功功率的稳定传输。
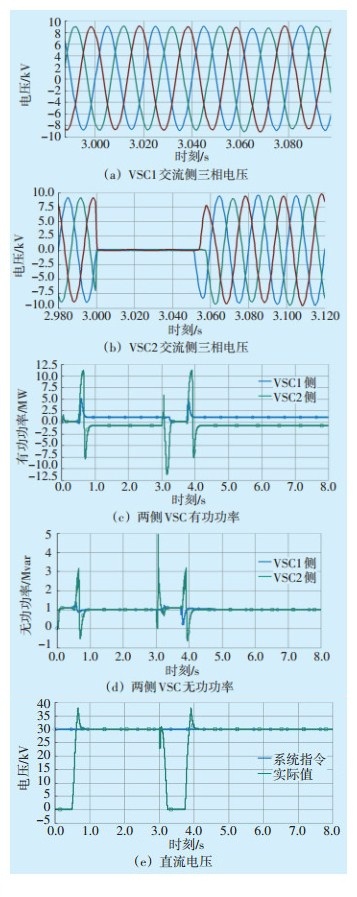
2.2.2 短路故障仿真为了进一步验证控制系统的抗负载扰动性能,在VSC2交流侧设置三相短路故障。故障发生在第3 s,持续时间0.05 s,仿真结果如图 7所示。由图 7可知,当VSC2交流侧发生短路故障时,只是使直流电压、VSC2侧的有功功率与无功功率产生波动,故障消除时,系统能够快速恢复正常运行;故障对VSC1侧的有功功率与无功功率均没有明显影响。
|
图 7 短路故障仿真 |
通过在PSCAD/EMTDC软件中的建模仿真,分析了SNOP系统的动态工作特性与暂态响应特性,据此可总结其在配电网中的实际作用有:
(1)SNOP能够快速、准确调控其传输的有功功率,可有效平衡馈线间的负荷;
(2)基于VSC的工作特性,SNOP能发出或吸收系统所需的无功功率,为系统提供灵活的无功补偿;
(3)SNOP可在一定程度上控制其交流侧的电压水平,能够有效改善其所连馈线的电能质量[4]。
目前电力电子技术在配电网中的应用较少,SNOP应用于具体工程还有很多技术和成本上的问题有待解决。随着柔性直流技术的不断成熟,将更加凸显SNOP的优势和实用性。
| [1] |
王成山, 孙充勃, 李鹏, 等. 基于SNOP的配电网运行优化及分析[J]. 电力系统自动化, 2015, 39(9): 82-87. |
| [2] |
孙充勃.含多种直流环节的配电网快速仿真与模拟关键技术研究[D].天津: 天津大学, 2015: 66-83.
|
| [3] |
于滢滢.基于锥优化的智能配电网优化问题建模方法研究[D].天津: 天津大学, 2014: 22-44.
|
| [4] |
李智诚, 吴建中, 和敬涵, 等. 软常开点的双闭环控制及其在配电网中的应用[J]. 智能电网, 2013, 1(1): 49-55. |
| [5] |
边国潮.利用柔性环网开关提高配电网光伏渗透率的研究[D].北京: 北京交通大学, 2016: 21-39.
|
| [6] |
吴俊勇, 裴丛仙子, 边国潮. 光伏并网配电网中柔性环网开关的优化运行控制策略研究[J]. 电工电能新技术, 2017, 36(9): 20-28. |
| [7] |
王成山, 宋关羽, 李鹏, 等. 基于智能软开关的智能配电网柔性互联技术及展望[J]. 电力系统自动化, 2016, 40(22): 168-175. DOI:10.7500/AEPS20160620009 |
| [8] |
秦红霞, 王成山, 刘树, 等. 智能微网与柔性配网相关技术探讨[J]. 电力系统保护与控制, 2016, 44(20): 17-23. DOI:10.7667/PSPC201663 |
| [9] |
杨欢, 蔡云, 屈子森, 等. 配电网柔性开关设备关键技术及其发展趋势[J]. 电力系统自动化, 2018, 42(7): 153-165. |
| [10] |
尹昌新, 朱洁, 蒋讯, 等. 多端柔性闭环中压配电网示范工程[J]. 电力系统及其自动化学报, 2019, 31(2): 66-73. |
| [11] |
王岸.SNOP的研究及其在配电网中的应用[D].北京: 北京交通大学, 2015: 22-26.
|
| [12] |
沈阳武, 彭晓涛, 孙元章. 背靠背双PWM变流器的协调控制策略[J]. 电网技术, 2012, 36(1): 146-152. |
| [13] |
肖世杰, 阙波, 李继红, 等. 基于模块化多电平换流器的柔性直流输电工程技术[M]. 北京: 中国电力出版社, 2018: 83-85.
|
 2020, Vol. 38
2020, Vol. 38 

