随着风电并网规模在内蒙古电网的日益增长,风电出力预测的准确性对电网运行的发供平衡及电力市场稳定经济运行的影响日益突出。风电出力预测按预测时间可分为中长期预测、短期预测及超短期预测。其中超短期预测指的是预测未来0~4 h的风电出力。超短期风电预测可分为物理计算法、统计学方法两类。物理计算法结合风场实际地形地貌,建立大气物理数学模型求解风机轮毂高度处风力变化[1-3]。统计学方法基于大量的历史数据并使用统计方法或智能算法预测风电出力,其中基于数据驱动和智能算法的预测技术已成为热点。文献[4]中提出马尔科夫链算法可在概率和波动特征上生成比实际序列更准确的预测序列。文献[5-6]结合卡尔曼滤波算法去除测量误差和系统误差,提高预测精度。常用的人工智能算法有神经网络算法[7-8]、支持向量机算法[9]、粒子群算法[10-11]、灰色模型法[12]等。其中BP网络神经算法具有自组织、自学习、自适应特性及很强的非线性函数逼近能力,是风电预测算法中较常见的一种方法[13]。文献[14]指出仅利用神经网络算法进行风电预测,可能出现随着隐藏层节点个数的增加导致过学习的情况,预测误差随之增加。同时利用单一的神经网络进行模型训练,计算精度稳定性差,往往会陷入局部最优解。
针对上述问题,本文将模拟退火算法(SA)、粒子群算法(PSO)与BP神经网络算法结合进行风电超短期功率预测,并以实际风机出力数据进行仿真,算例证明了改进后的BP神经网络具有更高的预测稳定性和预测精度。
1 风电出力的影响因素风机出力可表示为:
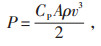
|
(1) |
其中,P为风轮输出功率,CP为风机转换效率,A为叶轮扫风面积,ρ为空气密度,v为风速。从式(1)可以看出,有多种因素影响P,v是主要影响因素,此外气温、气压影响ρ,风向影响A。
风电场的整体出力不能按统一的参数由式(1)简单累加多台风机的出力。因为风能经过上风向风机吸收后,其尾流会对下风向风机产生影响,同时由于各风电场地理特征的不同,地表粗糙度也会对不同位置的风机出力产生影响。
2 SA-PSO-BP神经网络风电预测算法 2.1 BP神经网络风电预测算法BP神经网络算法是一种基于误差逆向传播的多层前向神经网络算法,采用有监督式训练模式,学习存储大量的输入-输出模式映射关系,无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。
BP神经网络模型拓扑结构包括输入层、隐藏层和输出层,学习过程主要分为两个阶段,在初始化网络的结构和权值后,第一阶段是信号的前向传播,从输入层经过隐藏层,最后到达输出层;第二阶段是误差的反向传播,从输出层到隐藏层,再到输入层,依次调节隐藏层到输出层、输入层到隐藏层的权重,如果误差小于阈值或迭代次数达到上限则结束学习。BP神经网络结构如图 1所示。
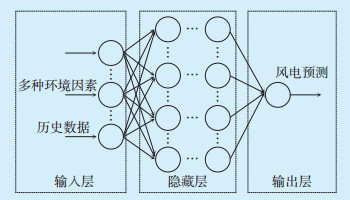
|
图 1 BP神经网络结构 |
粒子群优化算法(PSO)是一种通过群体合作搜索全局最优解的算法。由鸟群觅食活动获得启发,PSO在寻找问题最优解过程中,将求取的每个解作为一个粒子,用粒子群模仿鸟群,粒子自身搜索到的最优解称为个体极值,粒子群搜索的最优解称为群体极值,粒子的移动速度和方向由该粒子个体极值和群体极值决定,并在迭代搜索过程中不断更新,直至找到符合条件的最优粒子。
在一个n维搜索空间中,设置规模为m的粒子群x=(x1,x2,…,xm),粒子i的位置为xi=(xi1,xi2,…,xin),搜索速度及方向为vi=(vi1,vi2,…,vin)。则粒子i更新的速度和位置可由公式(2)、(3)求出:
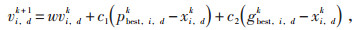
|
(2) |
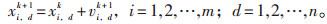
|
(3) |
其中,vi,dk和xi,dk分别为粒子i在k次迭代中第d维的速度和位置;pbest,i,dk为粒子在第k次迭代中第d维的最佳位置坐标;gbest,i,dk为第k次迭代中种群的最佳位置第d维坐标;w为惯性因子;c1、c2为学习因子。
定义适应度函数为:
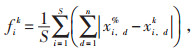
|
(4) |
其中,S为训练数据的样本数,xi,d%输出样本第d维的实际值,xi,d k为第k次迭代后第d维的输出值。基本计算结构如图 2所示。
|
图 2 粒子群优化算法结构 |
模拟退火算法(SA)来源于金属冷却过程,金属加热至高温后,若温度缓慢下降,则其内部原子运动逐渐减缓,最终形成低能量、结构稳定、排列均匀的高密度规则晶体,等效于搜索问题中的全局最优解。若温度骤降,内部原子尚未找到稳定位置,则形成能量较高、结构复杂、密度不均的非晶体,即局部最优解。SA通过自适应的速率控制解集的移动方向和尺度,使得所求解逐步靠近全局最优值,有效避免局部最优解问题。
SA包含两部分,即Metropolis算法和退火过程。Metropolis算法以一定概率接受劣解作为下次迭代的基础。同时高温退火过程即为粒子的高能量变异过程,使得SA能够跳出局部最优解。计算如下。
假设前一个解为X(n),系统根据某一指标计算得新解X(n+1),系统的能量由E(n)变为E(n+1),定义系统由X(n)变为X(n+1)的接受概率P为:
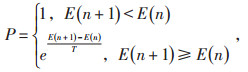
|
(5) |
式中T为温度。设温度T衰减速率为λ,即:
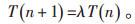
|
(6) |
SA基本流程如图 3所示。
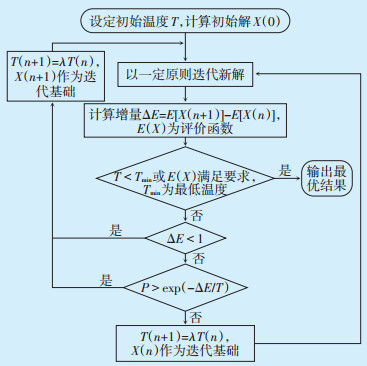
|
图 3 模拟退火算法结构 |
BP神经网络算法能够通过学习自动提取输入、输出数据间的“合理规则”,并自适应地将学习内容记忆于网络的权值中,同时具有较强的非线性映射能力。但从数学角度看,它是一种局部搜索的优化方法,它要解决的是一个复杂非线性化问题,这样会使算法陷入局部极值,同时BP神经网络对初始网络权重非常敏感,以不同的权重初始化网络,往往收敛于不同的局部极小值。
模拟退火混合粒子群算法(SA-PSO)通过集群协作、容纳劣解等方式跳出局部最优值,具有极强的全局搜索能力和极高的搜索效率,可将BP神经网络的初始权重作为种群粒子进行全局寻优调整,从而得到最优的网络参数,提高BP网络的预测精度。
本文采集内蒙古巴彦淖尔盟某风电场测风塔所测风速、风向、温度及该风场历史风电出力作为输入变量。为了减少奇异数据的影响并提高收敛速度,采用极值归一化方法,使用式(7)将输入数据归一化为[0, 1]。归一化后,输入数据用于训练BP神经网络的参数。
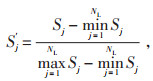
|
(7) |
其中,Sj为归一化前的参数,S′j为归一化后的参数。PSO搜索维度n为4,设种群规模m为8,粒子每次i方向上最大搜索距离vi,max为0.2,惯性因子w为1。为提高算法搜索范围,采用动态学习因子,r为[0, 1]内随机数,NL为风电场历史风电出力数据集。
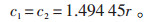
|
(8) |
设粒子群搜索迭代次数为10次,SA最高温度Tmax为10 000 ℃,最低温度Tmin为0.1 ℃,温度衰减系数λ为0.98。
设置针对该训练样本的8组随机粒子,即8组不同的神经网络参数集x=(x1,x2,…,x8),利用BP神经网络算法求取训练样本的预测值,并与实际风电场出力比较,由式(4)求取该粒子适应度。
设在温度为T(n)的第k次粒子群搜索过程中,如果粒子xik的适应度fik小于原第k次个体最优解pbestk适应度fp,bestk,则更新个体最优解,即pbestk = xik。如果粒子xik的适应度fik小于第k次搜索过程中找到的种群最优解gbest的适应度fg,best,则更新种群最优解,即令gbest= xik,否则以概率P接受xik为种群最优解gbest= xik,概率P表达式如下:
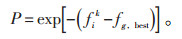
|
(9) |
利用利用公式(2)、(3)更新种群,同时设置变异概率为5%,随机更新某一粒子维度参数xj,dk,重新计算粒子适应度,继续第k+1次种群搜索。若最优粒子适应度满足要求,则停止搜索,否则粒子群搜索次数达到最大搜索次数10时,以式(6)更新模拟退火温度参数为T(n+1),开始新一轮粒子群搜索,直至最佳种群粒子适应度满足要求,或模拟退火温度参数T达到最小温度Tmin。具体计算流程如图 4所示。
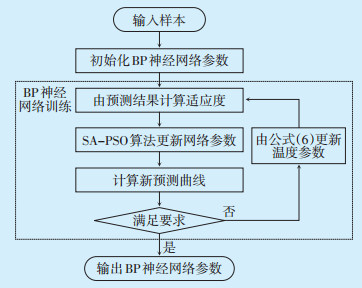
|
图 4 SA-PSO-BP神经网络算法结构 |
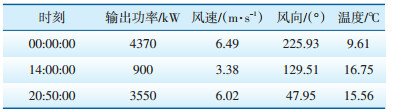
选取内蒙古巴彦淖尔市某风电场风机实测数据(数据类型见表 1)进行研究,该风场每台风机轮毂高65 m,叶片半径37.5 m,总容量为15 000 kW。训练数据为2019-05-27至2019-08-25连续91 d每10 min记录一组共计13 104组训练样本合集,测试数据是2019-08-26—2019-08-27的共288个测试样本集。虽然是对两日的风电出力进行预测验证,但由于改进后的BP算法输入的气象数据为当时环境实测值,精度接近于超短期风电预测使用的气象数据,故本例仍为超短期风电预测算例。
| 表 1 风机部分实测数据 |
根据以上训练数据,采用SA-PSO-BP算法进行超短期风电预测。图 5为风电出力的预测值和实际值对比曲线,图 6为训练样本及测试样本回归分析图。从图 5和图 6可以看出,风电出力预测值非常接近实际值,相关系数R接近1,说明采用的预测方法可提供令人满意的高精度预测结果。
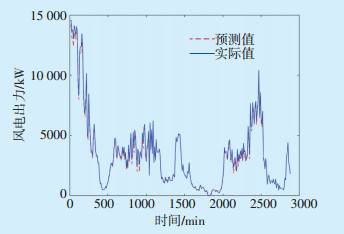
|
图 5 超短期风电出力预测值与实际值对比曲线 |
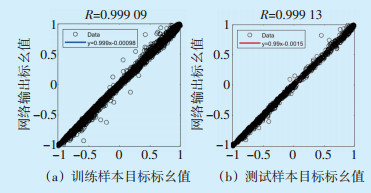
|
图 6 SA-PSO-BP神经网络训练样本及测试样本回归分析图 |
对以下3种预测方法进行仿真分析。
方法1:考虑多环境因素,基于SA-PSO-BP算法的超短期风电预测,与本文提出的策略相对应。
方法2:考虑多环境因素,在PSO-BP算法训练过程的情况下,基于BP神经网络的超短期风电预测。
方法3:考虑多环境因素,在BP算法训练过程的情况下,基于BP神经网络的超短期风电预测。
采用预测误差描述预测方法的预测效果。预测误差定义如下:
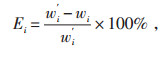
|
(10) |
其中,Ei是均值预测误差,w′i是风电出力实际值,wi是风电出力SA-PSO-BP预测值。
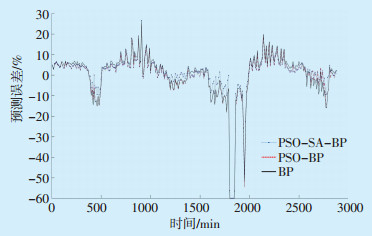
3种预测方法在每个时间段的均值预测误差如图 7所示。
|
图 7 3种方法预测误差对比 |
从图 7可以看出,在相同条件下,SA-PSO-BP算法的均值预测误差要小于其他2种方法,预测精度较高。说明SA-PSO-BP超短期预测提供了比传统BP预测方法更好的预测结果。
4 结束语本文综合考虑风电场出力影响因素,提出在BP神经网络参数训练过程中,利用PSO逐代更新粒子向最优解靠近,同时结合SA跳出局部最优陷阱,找到全局中优网络参数的超短期风电预测方法。并对巴彦淖尔市风场输出功率进行预测,验证了该预测方法的有效性,预测误差在10%左右。
该算法可以从以下方面进行改进:优化PSO学习因子自适应性,优化SA温度递减的自适应性,考虑更多的风电出力影响因素,进一步提高SA-PSO-BP算法预测精度和计算速度。
| [1] |
冯双磊, 王伟胜, 刘纯, 等. 风电场功率预测物理方法研究[J]. 中国电机工程学报, 2010, 30(2): 1-6. |
| [2] |
王一妹.基于CFD流场预计算的复杂地形风电场功率预测方法研究[D].北京: 华北电力大学, 2014.
|
| [3] |
王一妹.风电场尾流场与功率多精度模拟方法研究[D].北京: 华北电力大学, 2018.
|
| [4] |
蒋平, 霍雨翀, 张龙, 等. 基于改进一阶马尔可夫链的风速时间序列模型[J]. 电力系统自动化, 2014, 38(19): 22-27. |
| [5] |
刘晓洋.风速预测中数椐和样本的有效处理及其模型优化研究[D].太原: 太原理工大学, 2016.
|
| [6] |
杨明莉, 刘三明, 王致杰, 等. 卡尔曼小波神经网络风速预测[J]. 电力系统及其自动化学报, 2015, 27(12): 42-46. DOI:10.3969/j.issn.1003-8930.2015.12.08 |
| [7] |
杨茂, 周宜. 计及风电场状态的风电功率超短期预测[J]. 中国电机工程学报, 2019, 39(5): 1259-1268. |
| [8] |
马聪.基于BP神经网络优化的风电场短期功率预测研究[D].昆明: 昆明理工大学, 2017.
|
| [9] |
杨旭琼.基于最小二乘支持向量机的超短期风功率组合预测模型研究[D].长沙: 湖南大学, 2017.
|
| [10] |
孟庆霖.基于蚁群和粒子群算法的风电功率预测策略[D].天津: 天津大学, 2010.
|
| [11] |
杨志凌, 刘永前. 应用粒子群优化算法的短期风电功率预测[J]. 电网技术, 2011(5): 164-169. |
| [12] |
杨茂, 黄宾阳, 江博. 基于概率分布量化指标和灰色关联决策的风电功率实时预测研究[J]. 中国电机工程学报, 2017, 37(24): 7099-7107. |
| [13] |
师洪涛, 杨静玲, 丁茂生, 等. 基于小波-BP神经网络的短期风电功率预测方法[J]. 电力系统自动化, 2011, 35(16): 44-48. |
| [14] |
刘纯, 范高锋, 王伟胜, 等. 风电场输出功率的组合预测模型[J]. 电网技术, 2009(13): 74-79. |
 2020, Vol. 38
2020, Vol. 38