2. 内蒙古自治区高电压与绝缘技术企业重点实验室, 呼和浩特 010020
2. Inner Mongolia Enterprise Key Laboratory of High Voltage and Insulation Technology, Hohhot 010020, China
电力变压器是电网的重要组成部分,变压器正常运行对保障电力系统安全稳定运行至关重要。电力变压器常见的冷却方式包括油浸自冷(ONAN)、油浸风冷(ONAF)、强迫油循环风冷(OFAF)、强迫油循环水冷(OFWF)、强迫导向油循环风冷(ODAF)、强迫导向油循环水冷(ODWF)等。强迫油循环冷却方式冷却效率高,因此在变电站容量较大的变压器冷却系统被广泛采用。但是,强迫油循环冷却方式变压器所需维护量较大,不仅增加了变压器的运维成本,同时还面临着潜油泵故障导致变压器全停的风险[1]。因此仍需开展变压器其他冷却类型的研究工作。
目前,国内外的研究方法主要集中在考虑油阻、传热等解析算法配合经验公式计算,以及对绕组区域采用二维模型进行仿真计算。文献[2]中构建了换流变压器二维简化模型,分别采用有限元法和多物理场仿真方法计算了常温下的稳态温度场,计算结果验证了混合方法的准确性和有效性;文献[3-7]构建了绕组、铁心和油道的三维模型,通过有限元法分析得出了3个部位的温升分布。上述研究在仿真分析时忽略了散热器与外界空气、绕组撑条与垫块绝缘结构以及冷却系统散热器对变压器温度分布的影响。因此,针对变压器冷却系统的分析,研究一套切实可行的热点温升及温度场分布方法尤为必要[8]。本文以SFJZ9-150 000 kVA/220型ONAF变压器为研究对象,使用Solidworks三维建模软件,完成绕组模块、管道油路模块、片散冷却器模块模型的创建,并利用Fluent软件对3个模型流体场与温度场进行仿真计算。
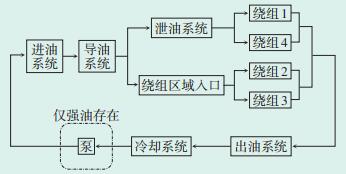
1 变压器冷却系统模型构建 1.1 变压器冷却系统划分对于大型变压器,其冷却系统包括冷却设备(冷却器及散热器)、导油系统(进油管路及储油管路)和绕组区域冷却油路等。油流网络如图 1所示,变压器的冷却系统串联、并联多个子系统,油路结构较复杂,导致数值计算模型计算量非常大[9-11]。目前,计算机的硬件水平很难对变压器冷却系统整体进行三维仿真计算,因此需要通过流体网络理论将其划分为几个部分进行有限元计算[12-15]。
|
图 1 变压器冷却系统油流网络 |
仿真分析所用变压器额定容量为150 000 kVA,冷却方式为ONAF/ONAN(100%/70%),主体尺寸7800 mm×2900 mm×3765 mm(长×宽×高),考虑高低压套管和片式冷却器后尺寸为9000 mm×7000 mm× 6880 mm,高压套管间距为2400 mm。在实际建模时,严格遵循该变压器尺寸,以使建模仿真结果趋于理想结果。
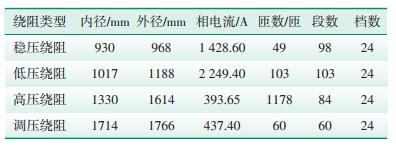
采用Solidworks软件创建的三维模型如图 2所示,所分析的部分为绕组模型、配油区域。其绕组参数见表 1所示。

|
图 2 片式散热风冷变压器三维模型 |
| 表 1 绕组参数 |
根据实际尺寸简化模型,得到图 3所示绕组实际比例模型。

|
图 3 变压器绕组整体剖面模型 |
在油浸风冷变压器模型中,下部绝缘中打通了与外部油箱中油的自由对流,该模型中油流驱动力为变压器油的浮升力。因此,线圈中油流速较慢,档位之间的油流量相似,可建立一档变压器线圈模型,如图 4所示。

|
图 4 绕组一档三维模型 |
在对变压器进行流固耦合计算时,需首先确定变压器冷却系统油流的流体分布计算控制方程,明确有限元计算的边界条件;在进行变压器冷却系统流体场流固耦合分析中,应分别确定流体与固体的物理特性,将边界条件与各种材料的物理特性输至Fluent软件中,通过有限元网格划分功能,针对控制方程进行有限元计算,得到计算区域流体场分布,进而进行热-流-固耦合计算,得到变压器冷却系统各点温度分布情况,以及变压器冷却系统温度场计算结果。
2.1 计算控制方程在变压器冷却系统流体场分布计算中,采用RNGk-ε模型计算湍流时,除了使用流体连续性方程与雷诺方程,还需建立湍动能的输运方程和一个湍流耗散率方程,近壁处采用双层模型处理[16]。
变压器绝缘油在油箱内的流动及其分布特性主要受质量守恒定律、动量守恒定律和能量守恒定律控制,如公式(1)—(3)所示:
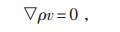
|
(1) |

|
(2) |
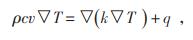
|
(3) |
式中:ρ为流体密度,kg/m3;v为流速,m/s;F为外部体积力,N;p为压力,N;μ为动力黏度,Ns/m2;c为比热容,J/(kg·℃);T为温度,℃;k为热导率,W/(m·℃);q为体积热源,W/m3,由绕组损耗得到。
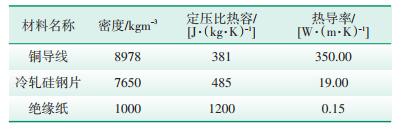
2.2 边界条件及材料物理特性设定变压器内部的铜导线、绝缘纸和冷轧硅钢片的密度、比热容、导热系数随温度的变化比较小,设为常数,如表 2所示。
| 表 2 固体材料热参数 |
线圈由多个线匝组成,线圈中铜和绝缘纸的热导率差别较大,则线圈的综合轴向热导率λa和综合径向热导率λr由公式(4)、(5)计算得出:
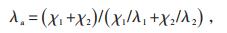
|
(4) |
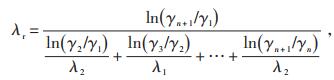
|
(5) |
式中:χ1,χ2—轴向铜导线和绝缘纸厚度,m;
λ1,λ2—铜和绝缘纸热导率,W/(m·℃);
γ1,γ2,…,γn+1—铜、绝缘纸、导线内半径,m。
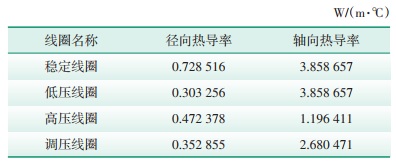
计算得到各线圈的综合热导率,见表 3。
| 表 3 线圈热导率 |
变压器油物理特性参数随温度的变化较大,可看作温度的函数,如表 4所示[5],出入口边界条件及热源条件设定如下。
| 表 4 变压器油物性参数的拟合输入公式 |
(1)出入口边界条件。变压器油流的驱动主要源于油经绕阻加热后的热升力,对其变压器整体油流冷却系统进行计算分析,确定冷却系统的运行工作状态,得到散热器出口温度和速度,近似为绕组入口温度和速度,作为绕组区域温度场计算的边界条件。
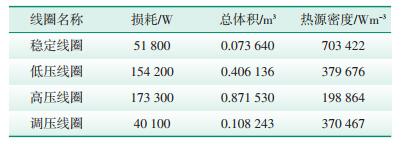
(2)热源条件。变压器中油的加热源为绕组线圈,其热源产热功率与线圈损耗功率一致,计算见公式(6),计算结果见表 5。
| 表 5 线圈热源密度计算结果 |
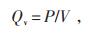
|
(6) |
式中:Qv—热源密度,W/m3;
P—损耗功率,W;
V—热源的体积,m3。
将材料物理特性和边界条件载入Fluent,采用有限元法计算变压器铁心绕组的热传导、油流温度速度场和流固耦合传热界面,体与体之间耦合面直接通过耦合边界的方式进行迭代计算。在对流换热过程中的热边界条件无法预先给定,而是受到流体与壁面间相互作用制约,通过计算得到变压器温度场分布和流体场分布。
2.4 计算结果分析对于油浸式变压器温度场建模仿真计算而言,温度场建模必须考虑散热器与风机、绕组撑条与垫块绝缘结构以及冷却系统散热器对变压器温度分布的影响。只有这样,仿真结果才能更接近实际。通常情况下,变压器温度场仿真计算主要采用热-流-固耦合分析方法以及对变压器器身部分与冷却回路的温度场、流体场分别仿真的方法。
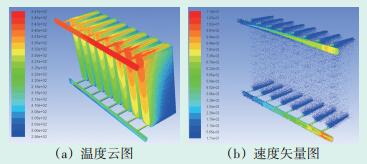
将上文所列出的计算控制方程、材料物理特性、有限元计算边界划分条件导入Fluent中的网格,将多组片式散热器进行排列组合,可得片式散热器温度云图和速度矢量图,如图 5所示。
|
图 5 片式散热器仿真分析图 |
冷却回路的总油阻力(ΔHZ),包括变压器本体的油阻力(ΔHT)和冷却器的油阻力(ΔHb),其中,ΔHT包括管道配流油阻力(ΔHg)和绕组内部油阻力(ΔHQ)。冷却回路的总油阻力按公式(7)计算:
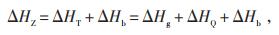
|
(7) |
式中:ΔHb与ΔHg可由冷却器速度矢量图得出,ΔHT = ΔHg + ΔHQ,通过ΔHT可得到绕组部分油流矢量分布。
计算得到变压器冷却系统速度矢量后,对于变压器绕组部分,由于其计算区域真实流量受到绕组部分压力影响,计算值与实际值往往存在偏差,因此需通过压力损失与流量的关系计算,对流量进行修正。
根据流体力学的计算公式可知,一般情况下,压力损失h与流量Q之间的关系可表示为式(8):
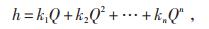
|
(8) |
式中:h为压力损失;Q为流量;k1,k2,…,kn为流量系数。
由大量文献实验验证,流量高次方项的系数接近于0[7-8]。利用最小二乘法原理分析流体阻力与流量的关系,流量三次方系数的数量级为10-3,因此可将公式(8)简化为h=k1Q + k2Q2。采用最小二乘法求出系数,将系数代入Fluent中修正ΔHQ,得到正确的ΔHT。
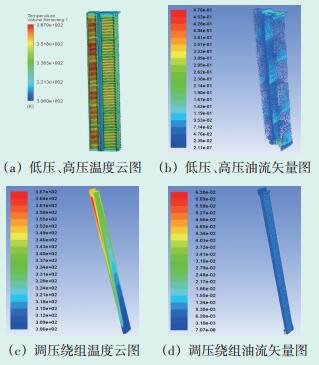
冷却油路入口管道配流部分,流体流速较快,因此采用紊流模型对入口管道配流部分进行求解。在采用变压器油作为冷却介质的大型变压器中,此部分可以忽略浮升力和重力的影响。计算得到绕组部分的温度分布以及油流分布,Fluent输出图像如图 6所示。
|
图 6 绕组流体场与温度场分布 |
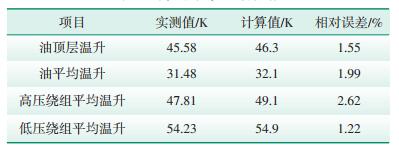
将仿真计算值与厂家试验数据进行对比,验证仿真结果的正确性,见表 6。
| 表 6 片式冷却温升数据 |
由表 6的数据可知:
(1)本方法所计算的绕组温度高于厂家试验得出的绕组温度,但是相对误差小于3%,符合工程设计要求,因此本文提出的变压器三维流体-温度场耦合仿真分析方法正确有效。
(2)造成仿真结果与计算结果误差的原因是变压器三维模型的简化以及变压器内部热源和热过程随着运行条件而变化的不确定性。
3 结束语本文介绍了一种基于有限元法的变压器三维流体-温度场耦合分析方法,以SFJZ9-150 000 kVA/220型油浸风冷(ONAF)变压器为算例,计算了该变压器绕组温度分布及变压器整体油流分布,将绕组温度计算结果与试验结果相对比,验证了该方法的正确性。
| [1] |
李英俊, 邢峰, 褚文超. 220 kV重负荷变压器强油风冷系统现场改造分析[J]. 内蒙古电力技术, 2019, 37(3): 47-51. |
| [2] |
刘刚, 靳艳娇, 马永强, 等. 基于混合法的油浸式变压器二维瞬态温度场仿真[J]. 高压电器, 2019, 55(4): 82-89. |
| [3] |
王磊, 王敏壕, 王倩, 等. 非晶合金变压器多物理场仿真及能效分析[J]. 变压器, 2018, 55(9): 32-38. |
| [4] |
张瀚方.基于非平均热源的换流变压器温度场仿真研究[D].北京: 华北电力大学, 2017.
|
| [5] |
廖才波, 阮江军, 陆云才, 等. 油浸式立体卷铁心变压器温度场仿真分析[J]. 变压器, 2016, 53(11): 41-44. |
| [6] |
卢冰原.基于流固耦合分析的海上风电变压器温度场仿真[C]//沈阳市科学技术协会.第十四届沈阳科学学术年会论文集(理工农医).沈阳: 沈阳市科学技术协会, 2017: 5.
|
| [7] |
唐宇.大型电力变压器附加损耗与温度场分析[D].哈尔滨: 哈尔滨理工大学, 2017.
|
| [8] |
张建瓴, 周壮广, 可欣荣. 基于分体解耦方法的变压器温度场模拟[J]. 广东电力, 2020, 33(1): 140-146. |
| [9] |
谢裕清.油浸式电力变压器流场及温度场耦合有限元方法研究[D].北京: 华北电力大学, 2017.
|
| [10] |
李龙女.自然油循环变压器的油流分布与温度场研究[D].沈阳: 沈阳工业大学, 2016.
|
| [11] |
阮江军, 段辞涵, 龚若涵, 等.变压器温度-流体场耦合分析网格剖分方法优化研究[J/OL].郑州大学学报(工学版): 1-6[2020-07-22].https://doi.org/10.13705/j.issn.1671-6833.2020.02.002.
|
| [12] |
杨增军.片式散热器自然油循环变压器温升研究[D].天津: 河北工业大学, 2004.
|
| [13] |
全国变压器标准化技术委员会.电力变压器第2部分: 液浸式变压器的温升: GB 1094.2-2013[S].北京: 中国标准出版社, 2014.
|
| [14] |
王秀春, 杨增军, 毛一之, 等. 自然冷却高燃点油变压器温升计算方法[J]. 中国电机工程学报, 2004, 24(7): 227-230. |
| [15] |
靳一林, 田双双, 邵翠玲, 等. 油浸式变压器的简化热路模型[J]. 变压器, 2015, 52(10): 38-42. |
| [16] |
赵蓉, 冯智倩, 高荣贵, 等. 油浸式变压器顶层油温热路模型计算分析与检验[J]. 电工电气, 2014(2): 56-60. |
 2020, Vol. 38
2020, Vol. 38