2. 内蒙古自治区电力系统智能化电网仿真企业重点实验室, 呼和浩特 010020
2. Inner Mongolia Enterprise Key Laboratory of Smart Grid Simulation of Electrical Power System, Hohhot 010020, China
随着内蒙古电网规模和供电需求的逐渐扩大,输电网络重载问题日益严峻,电力系统在暂态稳定之后的中长期动态过程的稳定性成为系统安全稳定运行的重要问题之一[1-3]。因此有必要对电网中长期动态稳定问题进行全面的仿真分析。
中长期动态仿真是电力系统受到扰动后较长时间的动态仿真过程,与暂态仿真不同的是仿真元件既包括暂态稳定仿真中所考虑的系统和元件,还需要计及电力系统中长过程、慢速元件的动态特性,这些慢速元件在仿真中对系统电压稳定起到重要作用[2-4]。本文采用电力系统全过程动态仿真软件(PSD-FDS)[5-6],在内蒙古电网数据中加入火电厂锅炉及其调速器模型、发电机过励磁限制器(OEL)和有载调压变压器(OLTC)[7-8]模型,分析其对电网稳定性的影响,总结提高电网中长期动态稳定性的措施,避免因慢速元件动作引起电网电压失稳。
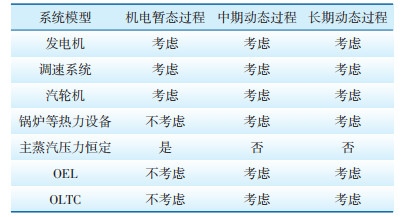
1 内蒙古电网中长期动态稳定计算分析根据仿真的时长和目的不同,系统中需要考虑的模型也不完全相同,表 1列出了机电暂态过程和中长期动态过程中分别需要考虑的一些重要模型。内蒙古电网负荷模型采用现有模式,即60%感应电动机负荷模型和40%的恒阻抗负荷模型(网架结构见图 1)。
| 表 1 不同仿真过程的数学模型和假设条件 |
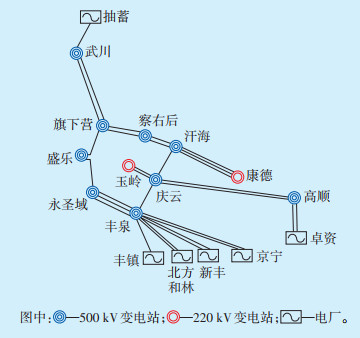
|
图 1 内蒙古电网部分网架结构示意图 |
在内蒙古电网所有发电机组中均加入OEL模型,模拟故障为:永丰Ⅰ回线路在0.2 s时发生三相短路故障,随后永丰Ⅰ、Ⅱ回线在0.3 s时首末端三相短路跳开,仿真时长为360 s。故障发生后,抽蓄电厂、新丰电厂、京宁电厂、丰镇电厂和卓资电厂的机组OEL相继动作。
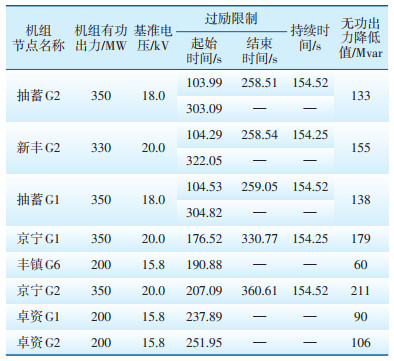
仿真结果如表 2所示,可以看出,在故障发生后,系统中多台发电机组相继发生了过励磁限制情况,相应机组的OEL开始动作。主要原因是呼丰断面的永丰Ⅲ回线路跳开后,大量潮流通过其他交流通道转移,导致沿途通道消耗大量的无功功率,线路损耗增加、相关节点电压跌落,因此沿途通道上各发电机组将运行在过励磁状态下,以增加其无功出力来提高相关节点电压。机组在过励磁状态下运行会产生大量热量,当发电机组中累积的热量达到极限值时OEL就会动作,从而限制过励磁电流,降低机组无功出力,保护发电机组。在仿真时间内,若发生过励磁限制的机组释放热量累加为零,过励磁限制动作结束后,电网中相关节点电压仍然较低,则机组可再次进入过励状态,直至OEL再次动作,如抽蓄G2、新丰G2等。
| 表 2 发电机组过励磁情况 |
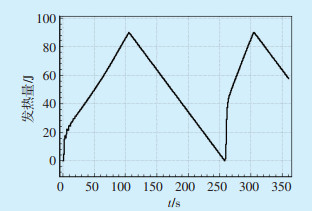
以抽蓄G2机组为例分析,故障发生后,抽蓄G2(18 kV)机组中热量曲线如图 2所示。为了对比说明OEL对机组动态稳定性的影响,分别仿真了抽蓄G2机组中加入和不加入OEL两种情况下的励磁电流和无功功率对比曲线,如图 3所示。
|
图 2 抽蓄G2机组热量曲线 |
|
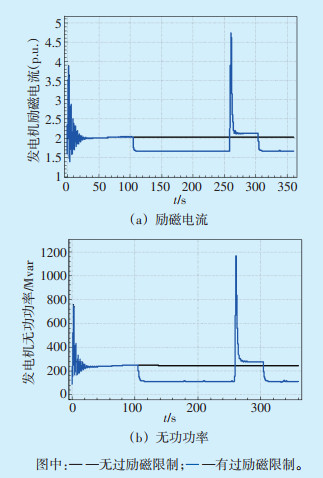
图 3 抽蓄G2机组励磁电流和无功功率曲线 |
结合图 2、图 3,在103.99 s时机组中累积的热量达到极限值,此时机组OEL第一次动作,电流从2.0(p.u.)降到1.7(p.u.),机组无功功率从244 Mvar降到111 Mvar。OEL第一次动作后,机组内累积的热量开始反向释放,在258.51 s时,热量释放至0,此时机组的OEL第一次动作结束。因机组母线电压仍较低,抽蓄G2机组的励磁电流和无功功率输出均会增加,试图恢复母线节点的电压至合理水平,但在303.09 s时机组中累积的热量再次达到极限值,因此OEL再次动作,限制机组的励磁电流和无功功率,机组的励磁电流和无功功率再次降低。随着抽蓄G2机组的OEL的动作和退出,机组的励磁电流和无功功率输出在短时间内不断变化,不再维持稳定。在仿真时间内,和无过励磁限制时比较,有过励磁限制时抽蓄G2发电机组少发133 Mvar的无功功率,降低了电网的电压稳定水平。
故障后,电网中加入、不加入OEL两种情况下,潮流转移通道上的500 kV站点电压变化对比曲线见图 4(以500 kV武川变电站、旗下营变电站为例)。
|
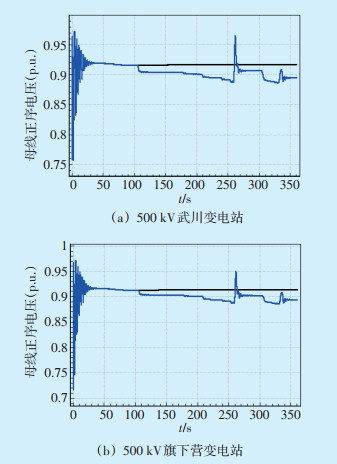
图 4 潮流转移通道上500 kV节点电压对比 |
在发电机中加入OEL模型后,电网相关节点的电压水平不再保持稳定,而是随着OEL的动作不断波动,在仿真结束后电压有所下降。特别是处于送电通道上的中枢点电压水平下降会更明显,如500 kV武川变电站和旗下营变电站,在仿真时段内,变电站电压未能恢复到0.9(p.u.)以上,不满足电压稳定要求。反映出OEL的正确动作虽达到了保护发电机的目的,但却使相关节点电压明显跌落,降低了系统的电压稳定水平。
1.2 OLTC模型对仿真结果的影响分析对乌兰察布地区的全部220 kV变压器施加有载调压手段,其220 kV高压侧分接头调整档位为230±8×1.25% kV,控制母线均选择其负荷侧,分接头动作延迟时间Td0=30 s。模拟故障为永丰Ⅰ回线路在0.2 s时发生三相短路故障,随后永丰Ⅰ、Ⅱ回线路在0.3 s时首末端三相短路跳开。
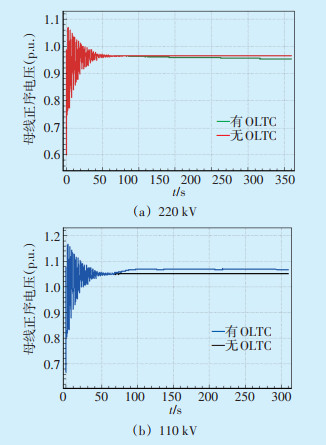
以康德220 kV变电站为例,图 5为加入和不加入OLTC的220 kV及110 kV节点电压曲线。OLTC分接头动作,使负荷端电压得到提高,负荷功率得以恢复。与未加入OLTC相比,变压器的220 kV侧电压稳定后的幅值变小,由0.96(p.u.)降低至0.95(p.u.),110 kV侧电压稳定后的幅值变大,由0.105(p.u.)升高至0.106(p.u.);110 kV节点电压在102 s左右达到了最高值,约为0.107(p.u.),稳定后的电压幅值维持在0.106(p.u.)左右。
|
图 5 康德变电站节点电压 |
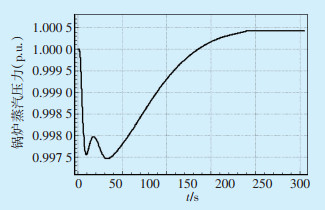
在内蒙古电网加入火电机组的锅炉及其调速器模型,比较分析其对内蒙古电网机组的影响。模拟0.2 s故障时北方和林电厂G2机组退出运行,以新丰电厂机组为例分析,新丰G1(20 kV)锅炉的主蒸汽压力曲线如图 6所示。故障发生后,由于北方和林电厂G2机组突然断开,造成系统有功功率不足,此时新丰G1发电机组会增大阀门开度,增加出力,来维持系统有功功率的平衡,这样就导致其锅炉的主蒸汽压力先减小,然后随着系统的再次平衡逐渐上升并维持稳定。
|
图 6 新丰G1锅炉的主蒸汽压力曲线 |
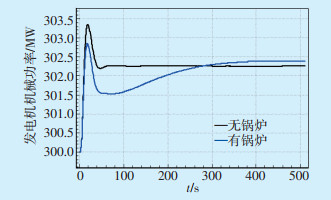
新丰G1有、无锅炉及其调速器模型的情况下,其机械功率曲线对比如图 7所示。可以看出,加入模型后,由于新丰G1发电机组的锅炉主蒸汽压力在扰动后先减小然后逐渐上升,导致新丰G1机组的机械功率减小;且在扰动后的前面几摆,新丰G1机组的机械输出功率不能像无锅炉模型时迅速跟踪系统需求,所以机组的机械输出功率跟随系统需求的能力也有所减弱。
|
图 7 新丰G1机组机械功率曲线 |
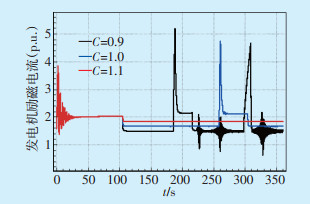
由1.1节仿真分析可知,OEL的动作不断波动,不利于系统稳定性。通过修改OEL模型中的参数,发现过励恢复系数C对仿真结果影响较大。令C分别为0.9、1.0、1.1,模拟故障同样为永丰N-3故障,以抽蓄G2机组和武川变电站为例分析,仿真结果如图 8、图 9所示。
|
图 8 抽蓄G2发电机励磁电流 |
|
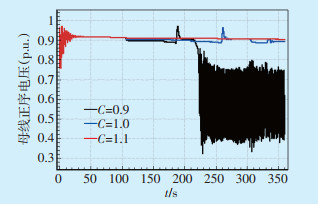
图 9 500 kV武川变电站电压 |
从对比结果可以看出,不同过励恢复系数对发电机发生过励限制有很大影响。当增大过励恢复系数时,发生过励限制的发电机组发生过励限制的频率减少,发生过励限制后励磁电流减小的幅值也在降低;相关节点的电压波动减小。因此,为了提高系统中长期动态稳定性,可适当提高过励恢复系数,避免因OEL频繁动作而降低系统电压稳定性。
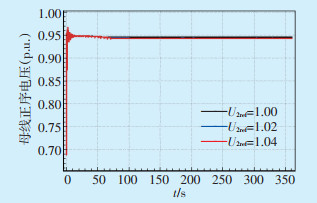
2.1.2 合理设置OLTC参考电压由1.2节仿真分析可知,OLTC分接头动作主要是为了使负荷侧电压升高,即增加负荷侧吸收的无功功率。当系统中无功储备不足时,分接头的不断动作会加剧电网的无功功率紧缺,降低系统中长期动态稳定性。通过修改OLTC模型中的参数,发现参考电压U2ref对系统电压影响较大。令U2ref分别为1.00(p.u.)、1.02(p.u.)及1.04(p.u.),分析其对仿真结果的影响。模拟故障同样为永丰N-2故障,仿真时间设为360 s,以玉岭220 kV变电站为例分析,仿真结果如图 10所示。
|
图 10 玉岭变电站220 kV节点电压 |
可以看出,参考电压设定越大,OLTC分接头动作后,使负荷侧母线电压达到设定值的同时,高压侧母线电压降低越严重。因此可将OLTC参考电压设置在合理范围,一般情况下设置为0.9~1.02(p.u.),在必要情况下闭锁有载调压变压器可以有效阻止系统进一步恶化。
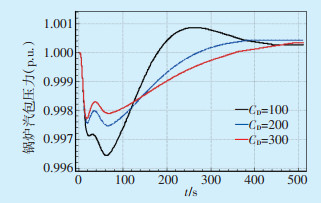
2.1.3 提高锅炉汽包存储时间常数由1.3节仿真结果分析可知,在加入锅炉模型后,火电机组的主蒸汽压力在扰动后不再保持恒定,机组的机械输出功率跟随系统需求的能力被削弱。通过修改锅炉模型中的参数,发现汽包存储时间常数CD对锅炉主蒸汽压力的影响较大。令CD分别为100、200及300,模拟0.2 s故障时北方和林1台机组退出运行,以新丰G1机组为例分析,仿真结果如图 11、12所示。
|
图 11 新丰G1锅炉的汽包压力曲线 |
|
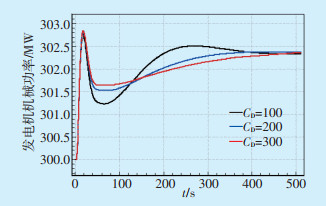
图 12 新丰G1机组机械功率曲线 |
可以看出,汽包存储时间常数影响锅炉蒸汽压力,最终导致发电机组出力不同。汽包存储时间常数越小,机组的响应速度越快,动态过程中主蒸汽压力波动越大,对系统功率需求的跟踪越不理想,对机组自身稳定运行越不利,严重情况下会损坏机组。因此在保证机组响应速度的前提下,可适当提高锅炉的汽包存储时间常数,有利于系统稳定性。
由仿真结果可知,通过优化各中长期模型的参数可提高系统动态稳定性,避免因参数设置不当而引起的系统稳定性变差甚至失稳问题。因此对于实际的OEL、OLTC等设备在投入使用前可通过仿真结果确定其最优参数,进行调试设置,而本节初步给出了各中长期模型对动态过程影响较大的参数及参数改变后对系统的影响程度,可为电网运行起到一定的指导作用。
2.2 配置保护装置提高系统中长期动态稳定性即提高系统的电稳定性,而OEL或OLTC的动作均能够引起系统无功功率不足,严重时可导致系统电压失稳。加装无功补偿装置是最直接有效的改善系统电压的措施,可以就近为负荷提供电压支撑,改善负荷节点的无功裕度。无功补偿器可以有效缓解当系统因OEL或OLTC时动作引起的无功功率不足。系统若具有快速响应切负荷[7, 9]装置或有一定的旋转备用容量[10-12],则当系统在中长期过程中因故障使系统潮流重新分配、无功损耗增加、电压降低而引起OEL或OLTC分接头频繁动作时,则快速响应切负荷装置可及时切除一定量的负荷,旋转备用容量也可以保证系统提供一定的有功支撑,维持功率平衡,有效防止电压失稳,提高系统可靠性[10-14]。
3 结论(1)本文基于PSD-FDS仿真软件,在内蒙古电网中加入火电厂的锅炉及其调速器模型、发电机OEL和OLTC模型等典型的中长期动态仿真模型,仿真分析了其对电网稳定性的影响。并提出了提高电网中长期动态稳定性的措施,即优化模型参数和配置系统保护装置,防止系统失稳。
(2)动态仿真全过程不仅能够提供大量的中长期动态仿真模型,而且仿真时间跨度大,采用了具有自动变阶、变步长功能的组合数值积分法,能够满足电力系统中长期动态仿真需求。
(3)电力系统中长期动态仿真中须加入必要的慢速动态元件,仿真持续时间较长,能够反映在一般暂态稳定仿真中不能反映的电压稳定问题,更好地模拟发生大扰动后发电机组在中长期动态过程中的特性,仿真结果更贴合实际电网的动态响应特性,发现暂态过程中难以发现的电压稳定问题。
| [1] |
孙景涛.中长期模型及参数对电压稳定的影响及控制措施研究[D].成都: 西南交通大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10613-1016177406.htm
|
| [2] |
曾雪松.基于PSD-FDS的电网中长期动态仿真[D].成都: 西南交通大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10613-1012391870.htm
|
| [3] |
陈刚, 范成围, 伍文城, 等. 中长期电压稳定时域仿真软件应用评估[J]. 中国电力, 2016, 49(10): 1-4. |
| [4] |
宋新立.电力系统全过程动态仿真算法与模型研究[D].天津: 天津大学, 2014. http://d.wanfangdata.com.cn/Thesis/D636234
|
| [5] |
汪滠, 牟宏, 刘晓明, 等. 电力系统全过程动态仿真技术综述[J]. 山东电力技术, 2017, 44(12): 1-3. |
| [6] |
宋新立, 王皓怀, 苏志达, 等. 电力系统全过程动态仿真技术的现状与展望[J]. 电力建设, 2015, 36(12): 1-4. |
| [7] |
霍启迪, 李晶, 唐晓骏, 等. 基于全过程动态仿真的受端电网中长期稳定轨迹特征及防控策略研究[J]. 电网技术, 2016, 40(8): 1-7. |
| [8] |
霍启迪.基于全过程仿真的城市电网中长期电压稳定轨迹特征及防控策略研究[D].北京: 华北电力大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10079-1017215008.htm
|
| [9] |
彭宗华.影响中长期电压稳定的负荷特性研究[D].北京: 华北电力大学, 2006. http://d.wanfangdata.com.cn/Thesis_Y867793.aspx
|
| [10] |
盛兴.大扰动下电压中长期稳定性的时域仿真研究[D].北京: 华北电力大学, 2009. http://d.wanfangdata.com.cn/Thesis_Y1796839.aspx
|
| [11] |
宋新立, 王成山, 仲悟之, 等. 电力系统全过程动态仿真中的自动发电控制模型[J]. 电网技术, 2013, 37(12): 1-3. |
| [12] |
宋新立, 陈英时, 王成山, 等. 全过程动态仿真中大型线性方程组的分块求解算法[J]. 电力系统自动化, 2014, 38(4): 1-3. |
| [13] |
邓裕文, 吴冠平, 毛卫东, 等. 中长期负荷预测的多因素模型研究[J]. 内蒙古电力技术, 2019, 37(3): 23-28. |
| [14] |
张芳, 仇雪芳, 李传栋. 电力系统中长期过程动态仿真的组合积分算法[J]. 电力自动化设备, 2017, 37(2): 113-120. |
 2020, Vol. 38
2020, Vol. 38