汽轮机是火电厂的主力机组之一,及时准确地掌握和预测机组运行状态,是保障机组及电网安全稳定运行的重要条件。通过开展汽轮机运行状态评价与预测研究,可全面了解机组实际运行情况,从多角度分析机组设备运行状态,明确故障情况对各类问题产生的影响;基于机组运行状态分析结果,可对机组故障属性、运行风险及维修方式等内容进行全面分析,有利于合理安排维护作业,高效、准确排除机组故障,改善电厂设备维护管理水平[1]。
汽轮机结构复杂,监测项目、测点数量众多,监测参数具有类型多、数量大及价值密度低等特点,符合大数据典型特征。基于大数据的机组状态预测方法,目前主要有高斯混合聚类模型[2-4]、线性随机方法(如自回归模型、移动平均模型、自回归移动平均模型等)[5-6]、灰色预测、模糊预测、神经网络预测、支持向量机预测等,后几种方法在处理非线性预测问题方面表现出了较好的性能,但应用中仍然存在一些不足[7]。基于高斯混合聚类模型是近年来发展起来的1种基于贝叶斯框架的新型概率预测方法,其基于1种独立的概率预测模型,预测结果具有概率意义。该方法对于处理非线性、高维数的复杂问题具有很好的适应性,得到了越来越广泛的应用[2-4]。本文基于汽轮机大数据,利用基于高斯混合聚类模型方法,实现了汽轮机状态预测。
1 设备运行状态预警模型的建立设备运行状态预警的准确性依赖于历史数据的质量及其包含的机组状态信息量,实际监测数据中存在不符合预期数据模式的异常值和离群值,因此本文提出的基于高斯混合聚类模型的状态预测方法,其建模流程为:首先利用相关性分析方法梳理和筛选出设备重要的监测参数,然后依据大数据平台的统计特征量进行样本数据预处理;再通过计算聚类个数的合适值,建立起最佳高斯混合聚类模型;最后基于该模型计算机组状态期望值与状态预警值,进行机组状态影响参数排序。
1.1 梳理和筛选设备监测参数依据机组监测要求和监测目标确定模型的输入参数,即机组实时监测参数,如介质温度、压力、流量、轴承振动等。实际机组监测时,应用相关性分析方法筛选出对设备安全状态影响较大的参数来重点监视、预警。
假设现有2个特征变量X、Y,其采集的离散数据时间序列分别为X1,X2,…,Xn和Y1,Y2,…,Yn,变量X、Y的皮尔逊相关系数ρX, Y计算式为:

|
(1) |
其中,cov(X,Y)为协方差,σX、σY分别为X、Y的标准差。
ρX, Y的绝对值越大,相关性越强;ρX, Y的绝对值越接近于0,相关性越弱。通常相关系数对应的相关程度如表 1所示。
| 表 1 相关系数对应的相关程度 |
基于大数据平台的历史数据采集组件,选择设备异动之后的时间段进行样本数据采集,同时避开设备缺陷过程时间段及前、后1~2 d,检修时间段及前、后1~2 d,系统自动计算出设备健康样本时间段,并基于健康样本时间段进行设备健康样本数据批量采集。采集频率依据样本量规模可设置为1~600 s,保证所有监测参数采集的同时性和连续性。
1.3 样本数据预处理确定健康样本数据S为N行P列,N代表样本记录个数,P代表样本变量个数。依据大数据平台的统计特征量组件计算样本数据的统计特征,包括:均值向量(Tavg1,Tavg2,...,Tavgp),最大值向量(Tmax1,Tmax2,...,Tmaxp),最小值向量(Tmin1,Tmin2,...,Tminp),极差向量(Tspan1,Tspan2,...,Tspanp),标准差向量(Tstd1,Tstd2,...,Tstdp),以及泊松相关系数矩阵Corre。依据相关系数矩阵各元素的值识别冗余监测参数,依据样本的极差向量、方差向量识别异常数据,最终确定用于模型计算的样本矩阵Si,并对样本数据按式(2)进行归一化处理:

|
(2) |
其中,xi为某个监测参数的实际值。
1.4 计算聚类个数的合适值对归一化样本进行聚类个数合适值计算,先给出聚类评价系数Coeff的定义:样本分为k类的类内距离之和dk_sum与样本分为l类的类内距离dl_sum之和的比值,即:

|
(3) |
式中:Mlj —样本分为l类时,某一类样本的均值向量第j列;
Tavgj —样本总体的均值向量的第j列;
l—样本分为k类时,某一类样本的样本数。
设定k值变化范围不小于1,且不大于样本记录个数的均方根(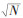
高斯混合聚类模型参数P(x)可表示为:

|
(4) |
该模型中有3个参数需要估计,分别是π,μ,Σ,式(4)可转化为:

|
(5) |
采用最大似然法(Expectation Maximization algorithm,EM)进行参数估计,其算法步骤为:
(1)指定π,μ,Σ的初始值。
(2)计算后验概率γ(Znk):

|
(6) |
(3)求解μk的最大似然函数:

|
(7) |
(4)求解Σk的最大似然值:

|
(8) |
(5)求解πk的最大似然函数:

|
(9) |
(6)重复步骤(2)—(5),直至算法收敛。
1.6 计算设备状态期望值按照样本聚类结果的标签矩阵IDX,以及样本按照高斯混合聚类模型分布的概率密度对数值向量L,求取各类样本点的联合概率密度自然对数值最大值,形成k个元素的列向量Lest,并将各类样本点的联合概率密度自然对数值最大值对应的样本点作为各类样本的期望值,k行P列期望值矩阵EST。
1.7 计算设备状态预警实时采集设备的1组监测数据即P维向量[X]l × p,基于高斯混合聚类模型计算其所属类别l及向量[X]l × p的联合概率密度自然对数值Lx,向量Lest第1个元素即为期望值的联合概率密度自然对数值Lest(l),期望值矩阵EST的第1行即为监测数据的期望值[Xest]l × p。
当实时监测数据的Lx大于Lest(l)时,健康度h定义为100%;当Lx小于Lest(l)时,健康度h计算公式为:

|
(10) |
当健康度小于设定限值hmin时,则给出设备状态监测预警。
1.8 设备状态影响参数排序基于设备监测向量[X]l × p与期望值向量[Xest]l × p的曼哈顿距离,进行设备各个监测参数偏离期望值对于设备状态的影响量计算。归一化设备监测向量及其期望值,得到设备监测向量(x1,x2,…,xp)与期望值向量(xest1,xest2,…,xestp),则某1个监测参数偏离期望值对于设备状态的影响量fi的计算公式如下:

|
(11) |
某监测参数fi越大,说明该参数异常对设备状态预警贡献程度越大。当出现设备状态预警时,对设备状态影响量计算结果按照降序排列,从而重点关注排序在前列的设备监测参数值及趋势,为设备状态诊断提供数据依据。
2 应用实例基于上述高斯混合聚类模型,开发了汽轮机运行状态预警系统,通过在某火电厂1号汽轮机组上实际应用,实现了该机组的安全状态预警。
2.1 监测参数的相关性分析该汽轮机组的主要监测参数包括:偏心、轴向位移、高中低压缸胀差、各轴承轴振瓦振、各轴承温度、主要蒸汽温度、缸温等,共计104个测点。为了监测汽轮机运行工况,以10 min为周期采集最近1 a内设备正常运行的历史数据,筛选掉机组负荷率低于30%及空值数据,利用统计特征量计算结果可以删除测量异常的参数,利用系统相关性分析进一步删除冗余监测参数。相关性分析结果如表 1所示。
表 2给出了106个参数的相关性分析结果,第1行和第1列中的字段如AI03316、AI03310……代表存储在实时/历史数据中的参数代码,其他数据为相应的相关系数值。从相关性极强(相关系数大于0.8)的多个参数中删除冗余参数,减少变量之间的线性相关性,最后保留了46个监测参数,即各轴承振动值、偏心、胀差、膨胀、轴向位移、轴封参数、润滑油温、润滑油压、密封油温、高中压部分缸温、低压缸抽汽参数、调节级出口金温、调节阀外壁金温等。
| 表 2 相关性分析结果 |
为确定聚类个数,利用系统聚类分析K值选取组件进行聚类个数探索,组件建模及K值选取组件设置截图如图 1所示。

|
图 1 聚类分析K值选取组件设置截图 |
依据样本条数的平方根确定K的最大值为62,进行模型计算后查看聚类效果指标随聚类个数的变化曲线,如图 2所示。确定出拐点值对应的聚类个数合适值为16,代表汽轮机转轴的16种典型工况模式。

|
图 2 聚类效果随聚类个数变化曲线 |
利用系统数据标准化组件基于K均值聚类模型进行聚类分析,得到聚类结果并将其设置为高斯混合聚类模型迭代初始值,具体建模设置如图 3所示。

|
图 3 K均值聚类建模设置 |
利用高斯MLLIB(Machine Learning Library)混合组件读取K均值模型聚类分析结果,并将其设置为高斯混合聚类模型的迭代初始值,如图 4所示。基于该设置,实现了高斯混合聚类模型的建立。

|
图 4 高斯混合聚类模型训练设置 |
完成高斯混合聚类模型训练后,将样本数据作为高斯混合模型的输入值,利用高斯MLLIB混合组件的预测算法计算监测数据的期望值、状态值及各监测参数对状态的影响值,计算结果见表 3。
| 表 3 高斯混合聚类模型计算结果1) |
基于样本工况的状态评价值中的较小数据,确定汽轮机转轴状态评价的稳健限值,结合现场经验暂采用四分位数方法[9]确定该限值。将样本数据的状态评价值按照从小到大进行排序,计算样本数据的状态评价值的第1个四分位数为70%。因而暂将70%作为汽轮机转轴监测工况的状态评价下限值,低于70%的汽轮机转轴监测工况状态则标记为预警状态,不低于70%的汽轮机转轴监测工况标记为正常状态。若设备预警状态持续一段时间(如10 min以上),则可以初步判定设备状态出现了早期劣化或故障征兆。
实时(每隔1 min)采集监测数据,基于高斯MLLIB混合组件的预测算法,计算监测数据的期望值、状态值及各监测参数对状态的影响值,并基于状态评价的下限值给出汽轮机转轴状态是否正常的提示;若汽轮机状态为预警状态,则依据各监测参数对状态的影响值(见1.8节)进行从大到小排序,可以分析出哪些监测参数对汽轮机转轴影响较大,从而进一步定位汽轮机转轴状态异常原因和处理措施,有效提升汽轮机转轴维护的及时性。
3 结语火电厂汽轮机组是1个庞大而复杂的系统,近年来AGC快速变负荷、灵活性改造等运行方式变化对机组运行状态的安全稳定性提出了更高的要求。本文基于机组大数据平台,通过对重要监测参数进行预处理,建立了最佳高斯混合聚类模型,可定量计算出机组状态期望值与状态预警值,实现了机组运行状态的早期预警,为保证机组安全状态评估、维修决策提供了参考依据。
| [1] |
陆颂元. 汽轮发电机组振动故障诊断及案例[M]. 北京: 中国电力出版社, 2016: 38-43.
|
| [2] |
冯振杰, 樊煜. 混沌时间序列的高斯过程混合模型预测[J]. 系统仿真学报, 2019, 31(7): 1387-1396. |
| [3] |
张磊, 李行善, 于劲松, 等. 1种基于高斯混合模型粒子滤波的故障预测算法[J]. 航空学报, 2009, 30(2): 319-324. |
| [4] |
刘哲.基于模糊聚类和高斯过程回归的光伏功率预测[D].广州: 广东工业大学, 2019. http://cdmd.cnki.com.cn/Article/CDMD-11845-1019890624.htm
|
| [5] |
刘颖, 严军. 基于时间序列ARMA模型的振动故障预测[J]. 化工自动化及仪表, 2011, 38(7): 841-843. |
| [6] |
XU H B. Fault identification of bearings based on bispectrum distribution of ARMA model and FCM method[J]. Journal of South China University of Technology, 2012, 40(7): 78-82. |
| [7] |
寇为刚, 李永祥, 孙艳军. 电力系统故障诊断的研究现状与展望综述[J]. 自动化与仪器仪表, 2015(2): 4-6, 9. |
 2020, Vol. 38
2020, Vol. 38 




