2. 内蒙古超高压供电局, 呼和浩特 010080
2. Inner Mongolia Extra-High Voltage Power Supply Bureau, Hohhot 010080, China
确定配电网无功补偿设备安装位置及容量的本质是非线性数学优化问题。解决此类问题,通常需要尝试不同场景下的多个解决方案,从中寻求最优解或近似最优解。现有研究大致可以分为两类,一类基于种群优化的方法(大部分研究都可归为此类[1-6]),如遗传算法[1-4]、人工蜂群算法[5]、Tab搜索算法及粒子群优化算法[6]等;另一类是数学规划方法,如混合整数编程算法[7]。这些方法通常以降低系统能耗为目标,配置方案虽然能够提升系统的经济效益,但对系统电压的改善效果有限。为了解决上述缺陷,本文针对在辐射型配电网的潮流算法基础上,提出一种基于遗传算法的改进型优化配置算法,并在1.0 IEEE-33节点测试模型上对该算法的有效性进行验证,为无功补偿设备的合理配置提供依据。
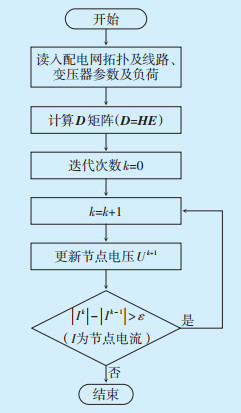
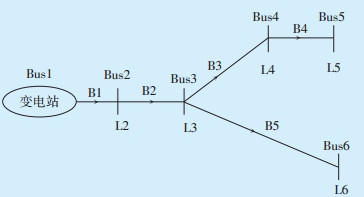
1 辐射型配电网的潮流算法目前电力系统稳态分析有多种潮流算法,如高斯-赛德尔算法、牛顿-拉夫逊算法及快速解耦算法等。但上述算法都是围绕输电系统建立的,虽然运算精度高,但需要求解大量非线性方程,计算过程复杂。与输电系统相比,配电网的R/X比值更高,采用上述方法,运算收敛性可能降低。另外电容器优化配置问题需要进行多次潮流计算,对算法的性能及稳定性要求更高。因此本文采用文献[8]中的潮流计算方法,根据配电网的拓扑结构生成支路电流-节点注入电流矩阵(以下简称E)和节点电压-支路电流矩阵(以下简称H),通过多次迭代得出潮流计算结果。配电网潮流算法的计算流程如图 1所示。以下通过1个6节点配电网络进行介绍。图 2为1个6节点的辐射型配电系统。
|
图 1 配电网潮流算法流程图 |
|
图中:Bus1—Bus6为节点;B1—B5为线路;L2—L6为负荷。 图 2 6节点辐射型配电系统结构示意图 |
首先建立支路电流-节点注入电流方程组:
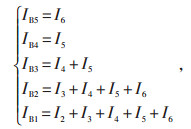
|
(1) |
式中:IBi —i支路电流;
Ij —j节点电流。
通过式(2)计算Ij:
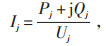
|
(2) |
式中:Pj —j节点的有功功率;
Qj —j节点的无功功率;
Uj —j节点的电压。
利用支路电流-节点注入电流方程组生成矩阵B:
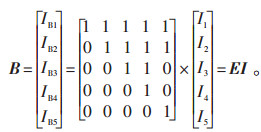
|
(3) |
然后建立节点电压-支路电流方程组:
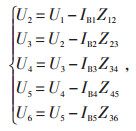
|
(4) |
式中:Zij—节点i,j之间的阻抗。
进而通过式(5)得出H:

|
(5) |
式中:ΔU —第一个节点的电压U1与其他节点电压差的向量。
结合式(3)有:
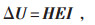
|
(6) |
取D = HE,则有ΔU = DI。
2 基于遗传算法的无功补偿设备优化配置若并联电容器的安装位置及容量均由遗传算法确定,则需要进行多次潮流计算,严重降低优化配置算法的计算效率[9-12]。本节首先提出能耗敏感度因子,利用该因子选出补偿设备的候选节点集合,而遗传算法只负责确定无功补偿设备的容量。
2.1 能耗敏感度因子节点能耗敏感度因子(Loss Sensitivity Factor,以下简称L)是评估节点安装无功补偿设备后节能效果的指标。L越大,节能效果越明显。
假设电流由i节点流至j节点,则线路k的有功损耗为:
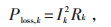
|
(7) |
式中:Rk及Ik分别为线路k的电阻和电流。Ik2由式(8)计算:
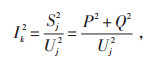
|
(8) |
式中:Sj为从i节点流入j节点的视在功率,因此:
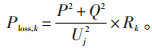
|
(9) |
则j节点的能耗敏感度因子Lj为:
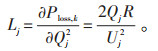
|
(10) |
从公式(10)可以看出,Lj即为线路k有功损耗对j节点无功功率的偏微分。根据L确定无功补偿候选节点的方法如下。
步骤1:首先进行潮流计算,利用公式(10)计算除配电网络外部节点外,各节点的能耗敏感度因子;
步骤2:将各节点按照能耗敏感度因子由高到低排列,生成(Li,Ui)序列;
步骤3:从第1个元素开始,遍历(Li,Ui)序列,当该节点的电压Ui低于最低允许电压U0(取0.94)时,该节点作为无功补偿候选节点,加入候选节点集合C,当C中元素个数达到预先设定的候选节点总数时,计算终止。否则继续访问(Li,Ui)序列下一元素,直到序列全部访问结束,最终返回C。
2.2 适应性函数遗传算法是一种通过模拟自然进化过程搜索最优解的方法,其从代表问题可能潜在的解集的初代种群开始,按照适者生存和优胜劣汰的原理,逐代演化适应性更强的个体。为了保证适应性更强的个体在新一代种群中出现,需要定义适应性函数,并通过特定的选择机制,保证适应性高的个体以大概率被选出。适应性高的个体通过交叉和变异,产生代表新的解集的种群。当种群的适应性收敛时,停止创建新的个体。末代种群中的最优个体经过解码可以作为问题近似最优解。
适应性函数(Fitness Function,以下简称F)的选取主要取决于优化目标,本次首要目标是提升配电网的电压合格率,其次是降低系统损耗,所以F由两部分组成:
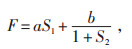
|
(11) |
式中:S1 = min(U1,U2,…,Un),Un为第n节点的电压;S2为系统8760 h总损耗,其计算方法见式(12):
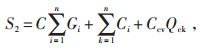
|
(12) |
其中,a,b为权重因子,相对于系统损耗,供电电压直接影响用户的安全生产及用电体验,故选取a= 0.7,b=0.3;C为电价,取0.5元/kWh;Gi为线路i的线损;Ci为第i号电容的安装成本,元;Ccv为无功补偿设备的单位容量的价格,取50元/kvar;Qck为无功补偿设备总容量,kvar。
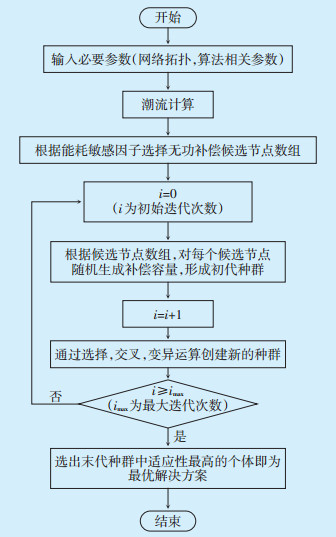
2.3 优化配置优化配置算法工作流程如图 3所示,首先输入基础数据进行潮流分析,得出安装无功补偿设备的候选节点集合。利用候选节点集合,随机生成各节点补偿容量,创建初代种群。利用遗传算法选出末代种群中适应性最强的个体即为无功补偿设备的近似最优配置方案。
|
图 3 基于遗传算法的无功补偿设备优化配置算法流程 |
本文利用Python程序语言实现无功补偿设备优化配置算法。与C++及Java语言相比,Python语言具备强大的数值计算能力且语法更为简单。
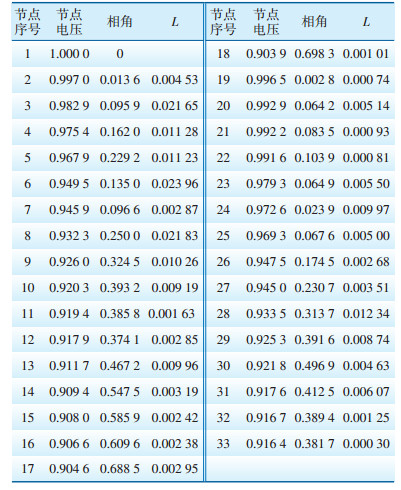
本次取1.0IEEE-33节点测试模型。首先利用第2节提出的配电网潮流算法进行计算,得出各节点电压(如表 1所示),多个节点电压均在0.93以下,电压最低的节点为18节点(0.903 9),低于允许的供电电压范围。利用式(8)计算各节点敏感度因子L,并按照降序排列,得出节点序列为(6,8,28,5,9,13,10,…)。假设无功补偿候选节点个数分别为5个、6个和7个,则候选节点数组分别为[6,8,28,5,9],[6,8,28,5,9,13],[6,8,28,5,9,13,10]。
| 表 1 初始潮流计算结果 |
以5节点补偿方案为例,设置遗传算法种群规模为50个,进化次数为20代,交叉和变异的概率分别为0.85和0.25。首先构建初代种群,初代种群中个体的补偿容量随机产生,在[100,1200](数值单位为kvar)范围内为每个节点随机生成补偿容量,得到1个5元素的数组[954,682,339,750,287],即在6,8,28,5,9节点分别安装容量为954 kvar、682 kvar、339 kvar,750 kvar,287 kvar并联电容器。该数组即为1个初代个体,重复使用该方式创建个体,当个体数达到50时,初代种群构建完毕。通过式(12)计算每个个体的适应性,为了将提升供电电压质量作为优化配置的首要目标,取a=0.7,b=0.3。本例使用了锦标赛选择策略以增大高适应性的个体被选中参与构建下一代个体的概率。锦标赛选择策略在进化过程中随机选取2个个体,适应性较高的个体作为交叉及变异的潜在对象。假设[1060,608,253,268,400],[954,682,339,750,287]2个个体被选中,通过创建随机数的方式确定交叉点,假设交叉点为2,则在第3个元素位置进行交叉运算,得出2个子代个体[1060,608,339,750,287]及[954,682,253,268,400]。变异针对单个个体,假设[1060,608,253,268,400]被选中进行变异运算,假定变异只能在单个元素上发生,通过创建随机数选择变异元素,假设变异位置为4,则重新随机生成第5个元素,获得新的子代为[1060,608,253,268,361]。
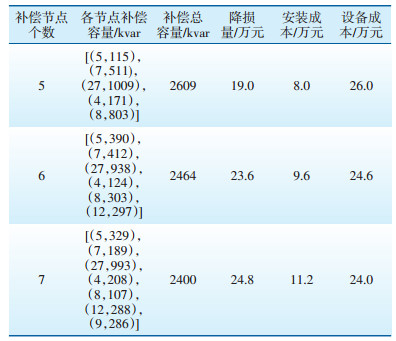
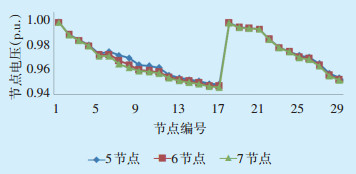
利用遗传算法,得出5节点、6节点和7节点优化配置方案的经济效益及电压曲线,比较结果见表 2和图 4。从表 2可以看出,通过安装并联电容器,3种方式均可有效降低系统有功损耗,在3 a内即可回收投资成本。
| 表 2 3种补偿方案比较 |
|
图 4 3种补偿方案节点电压 |
从图 4可以看出,3种方案对电压的改善效果均可满足要求,最低节点电压在0.94(p.u.)以上,满足10 kV供电电压要求,而6节点和7节点方案的经济性明显优于5节点方案。考虑节点多对应的运维工作量大,最终选取6节点电容器补偿方案。对原方案进行圆整处理后,得出最终的6节点配置方案为[390,410,940,120,300,300]。
上述针对最大负荷方式得出了无功补偿设备优化配置方案,而采用一般负荷及最小负荷方式时,系统电压基本均在正常区间,故本文重点针对大负荷方式进行无功补偿设备优化配置方案计算。
4 结束语本文提出一种综合考虑节能降耗与提升系统电压质量的无功补偿设备配置优化算法,并利用IEEE-33节点测试模型对该算法进行了测试。测试结果表明,优化配置算法能够满足工程应用需求。另外需要指出,本算法目前只对同一电压等级的配电系统进行了测试,未在包含多个电压等级的配电网络中进行测试;其次考虑到随着分布式电源渗透率逐渐增大,潮流可能发生改变,由此可能导致并网点电压的大幅波动,需要对优化配置算法进行修改和扩展,使其能够适应多电压等级及包含分布式电源的配电网潮流分析。
| [1] |
王庆斌, 刘涌, 杨昀, 等. 含分布式电源的10 kV配电网无功电压控制方法[J]. 电力电容器与无功补偿, 2018(2): 125-130. |
| [2] |
高梓维.中低压配电网无功电压补偿协调优化方法的研究[D].沈阳: 沈阳工程学院, 2019. http://cdmd.cnki.com.cn/Article/CDMD-11632-1019233470.htm
|
| [3] |
Kanwar N, Gupta N, Niazi K R, et al. Optimal distributed generation allocation in radial distribution systems considering customer-wise dedicated feeders and load patterns[J]. Journal of Modern Power Systems and Clean Energy, 2015, 3(4): 475-484. DOI:10.1007/s40565-015-0169-0 |
| [4] |
Lohia S, Mahela O P, Ola S R. Optimal capacitor placement in distribution system using genetic algorithm[C]//2016 IEEE 7th Power India International Conference (PIICON). IEEE, 2016.
|
| [5] |
Elsaiah S, Benidris M, Mitra J. Analytical approach for placement and sizing of distributed generation on distribution systems[J]. IET Generation, Transmission & Distribution, 2014, 8(6): 1039-1049. |
| [6] |
Rao R S, Narasimham S V L, Ramalingaraju M. Optimal capacitor placement in a radial distribution system using Plant Growth Simulation Algorithm[J]. International Journal of Electrical Power and Energy Systems, 2011, 33: 1133-1139. DOI:10.1016/j.ijepes.2010.11.021 |
| [7] |
Kazeem B, Alor M, Okafor E N C. Optimal placement of distributed generation in power distribution systems using neuro-genetic Algorithm[C]//2017 IEEE 3rd International Conference on Electro-Technology for National Development (NIGERCON). IEEE, 2017.
|
| [8] |
Prasanna K M L, Somlal J, Ranjithkumar R J, et al. Load flow studies for distribution system with and without distributed generation[J]. Water & Energy International, 2015, 57: 34-38. |
| [9] |
杜子敏. 配电网无功补偿设备原则及现存问题[J]. 中国高新技术企业, 2015(36): 139-140. |
| [10] |
常栋梁, 何立柱, 李洋, 等. 配电网功率平衡调节与无功补偿研究及装置[J]. 电力系统及其自动化学报, 2019, 31(4): 132-138. |
| [11] |
刘日彪, 刘曦, 周翰泽, 等. 10 kV配电网无功补偿方式的研讨[J]. 电工技术, 2016(12): 25-26, 40. |
| [12] |
季斌炜, 陈潇一. 基于粒子群算法的配电网无功补偿方法研究[J]. 电网与清洁能源, 2016, 32(3): 111-114. |
 2020, Vol. 38
2020, Vol. 38