2. 天津理工大学天津市复杂控制理论与应用重点实验室, 天津 300384
2. Tianjin Key Laboratory for Complicated Control Theory and Application, Tianjin University of Technology, Tianjin 300384, China
二极管中点钳位型(Neutral Point Clamped,NPC)三电平逆变器因具有良好的性能及其拓扑结构对硬件的要求较低等优点被广泛应用于高电压大功率场合[1]。空间矢量脉宽调制(SVPWM)技术以其易于数字实现,电压利用率高等特点,在三电平调制策略中得到迅速发展[2-5]。但其算法计算量过大,给控制器带来了额外负担;同时,三电平逆变器存在直流侧中性点电压波动问题。
近年来,很多学者针对以上问题进行研究,给出了不同的解决方案。文献[6-7]在60°坐标系的基础上,通过坐标变换、旋转模型、整数化计算等方法来简化算法;文献[8]在采用60°坐标系简化算法的同时考虑中点电压波动问题,以调节小矢量作用时间平衡中点电压。
本文在上述文献基础上,以60°坐标系为基础,研究三电平逆变器中性点电压平衡调制策略,同时讨论适用该策略的调制比区域。
1 简化的SVPWM算法三电平逆变器正常工作时每相桥臂有3种有效开关状态,分别为P、O、N,可以产生27种开关状态组合,对应27个空间电压矢量[9]。
三电平逆变器SVPWM算法根据最近3矢量原则计算:首先判断参考电压矢量所在位置;选择3个基本电压矢量,再根据伏秒平衡原理计算每个基本矢量的作用时间;最后选择合适的开关序列触发脉冲[10-11]。通过坐标变换,将传统90°坐标系转换为60°坐标系后,将参考电压矢量进行标幺化处理,再构建扇区旋转模型,将所有区间都旋转到第一大区间内,实现算法的优化。
1.1 坐标变换建立60°坐标系(g-h坐标系),设参考电压矢量Vref在g-h坐标系下的坐标为(Vg,Vh),在平面直角坐标系下的坐标为(Va,Vb,Vc),根据线性关系和Clark变换可以得到变换模型为:
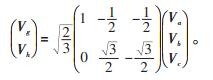
|
(1) |
为进一步简化算法,对Vref进行归一化处理。设六边形的最大值为Vmax,定义Vref=Vmax/2,实现所有电压矢量归一化。三相相电压可以表示为:
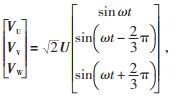
|
(2) |
式中:ω——角速度;
t—时间;
U—电网相电压有效值。
将式(2)带入式(1)可得:
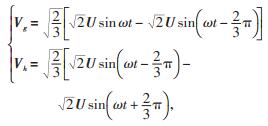
|
(3) |
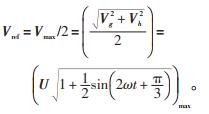
|
(4) |
当ωt=kπ+π/12(k为常数)时,sin(2ωt+π/3)=1,此时Vref的值为:
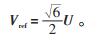
|
(5) |
经过电压矢量归一化处理后可得:
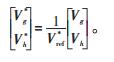
|
(6) |
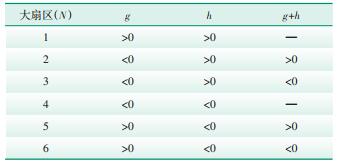
以g轴逆时针旋转,定义每60°为一个大扇区,扇区号依次为1,2,…,6,根据Vref在60°坐标系下的坐标(g,h)值的正负关系,即可确定Vref所处的大扇区位置,见表 1。
| 表 1 60°坐标系SVPWM算法大扇区判断原则 |
在判断Vref所在的小扇区之前,采取旋转的方式将其他大扇区中的Vref旋转(N-1)×60°到1号大扇区,第2大扇区Vref旋转到第1大扇区的示意图如图 1所示。扇区旋转模型具体转换关系见表 2。
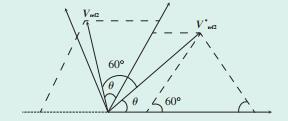
|
图中:Vref2—第2大扇区Vref;V *ref2—旋转至第1大扇区的Vref2。 图 1 旋转模型 |
| 表 2 大区间旋转变换原则 |
利用扇区旋转模型就只需讨论第1大区间的位置关系。将第1大区间划分为6个小区间,如图 2所示。
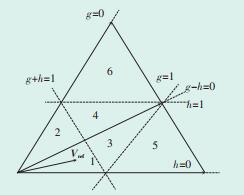
|
图中:Vref在小区间表示为Vref*。 图 2 小扇区划分 |
为方便判断,选取g+h=1,g-h=0两条线来辅助判定Vref。根据图 2所示数量关系,可以得到Vref的小区间位置,见表 3。
| 表 3 小扇区判断原则1) |
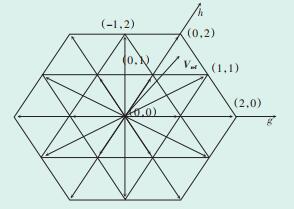
60°坐标系下所有基本矢量的坐标均为整数,因此对于任意的Vref,都有距离最近的4个基本矢量,如图 3所示。图中Vref对应的4个基本矢量为:
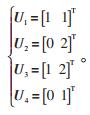
|
(7) |
式(7)中,U1、U2、U3、U4都为参考电压矢量在坐标系上取整所得,根据最近三矢量原则可选U1、U2为基本矢量,则第3个基本矢量就在g+h所在对角线上。当g+h>0时,U3为第3个最近的基本矢量;当g+h < 0时,U4为第3个最近的基本矢量。图 3中Vref的3个最近基本矢量为[1 1]T,[0 2]T,[0 1]T。
|
图 3 60°坐标系SVPWM空间电压矢量图 |
确定了3个基本矢量后,根据伏秒平衡原理可得:
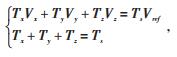
|
(8) |
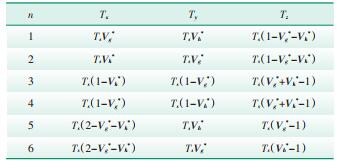
式中:Vx、Vy、Vz为合成参考电压矢量Vref的3个基本电压矢量;Vx、Vy、Vz分别为Vx、Vy、Vz在一个采样周期Ts中基本电压矢量对应的作用时间。Vref在第1区间各小区间的电压矢量作用时间见表 4。
| 表 4 基本矢量作用时间 |
本文在遵循开关状态转换原则即开关状态不能跳变,不能从p直接到n,只能是p到o或者n到o的前提下,尽量降低开关频率。生成7段式脉冲序列,以图 4为例各开关状态顺序为:零低低—零零低—零零零—高零零—零零零—零零低—零低低。
|
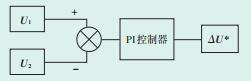
图 4 中点电压平衡控制PI控制器 |
三电平逆变器中性点电压平衡时,每个开关管承受的电压为直流电压的一半,若直流电容电压不平衡,则开关管承受的电压不均等,严重情况下可能损坏开关器件,导致输出谐波含量增大[6]。因此,研究三电平逆变器的中性点电压平衡问题十分重要。
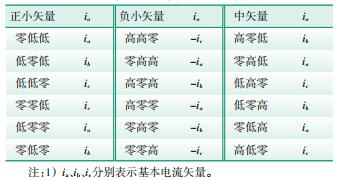
2.1 中性点电压不平衡原因中性点电流io、直流侧电容电压差共同决定中性点电压不平衡度。设中性点电压变化率ΔUnp=io/ 2C(C为电容),得到电容中性点电流与各电压矢量状态的关系,如表 5所示[12-13]。
| 表 5 基本矢量作用时间 |
由表 5可知,零、大矢量不影响中性点电压,中矢量对中性点电压的影响不可控,正、负小矢量产生的影响相反,可抵消。
2.2 中性点电压平衡控制策略由2.1节分析可知,可通过调整小矢量作用时间来控制中点电压。调整小矢量作用时间时要考虑中点电流io的方向及电容电压差ΔU的大小两个因素。定义ΔU=U1-U2,U1为上电容电压,U2为下电容电压。
本文采用的首发矢量均为正小矢量,首先检测io的方向。定义当io>0时,视为下电容放电,上电容充电。当io < 0时,视为下电容充电,上电容放电。获取io后,根据其对应的上下电容充电关系,调整首发矢量的作用时间。
设计1个PI控制器,如图 4所示。该PI环路的输入值为ΔU=U1-U2,定义PI默认值ΔU*为0.5。通过检测io的方向,根据ΔU的大小,调整正小矢量作用时间,即改变PI控制器的大小,以平衡中性点电压。
该PI环路的调节过程具体分析如下[14]。
(1)当U1 < U2,即ΔU < 0时,PI输出趋向于一个负值,将默认值0.5减小。此时判断io的方向,当io>0时,减小正小矢量作用时间;反之增加正小矢量的作用时间。
(2)当U1>U2,即ΔU>0时,PI输出趋向于一个正值,将默认值0.5增大。此时判断io的方向,当io>0时,增大正小矢量的作用时间;反之减小正小矢量的作用时间。
至此,设计的PI控制器已基本完成平衡中性点电压的要求。
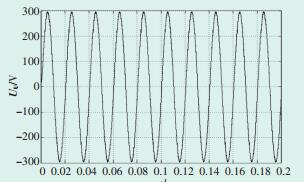
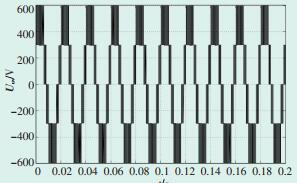
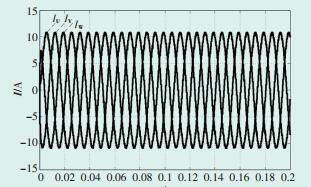
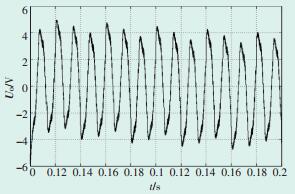
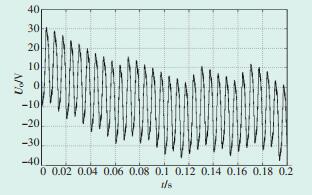
3 三电平逆变器控制策略仿真验证在Matlab/Simulink环境下搭建三电平逆变器中性点电压平衡控制策略模型。所采用的仿真参数为:直流侧输入线电压U=600 V,直流分压电容C1= C2=4700 μF系统运行仿真频率f=50 Hz;三相对称负载R=10 Ω,电感L=15 mH。图 5、图 6、图 7分别为输出侧U相电压、UV线电压及输出侧三相电流,其波形与传统SVPWM算法类似;图 8是当调制比m=0.3时的中点电压波动图,其幅值波动在±6 V之间;图 9是当m=0.8时的中点电压波动图,其幅值波动较大且波形不平稳。由此可知,文章所用算法在低调制比时可以基本平衡中点电压,但在高调制比下平衡效果较差。
|
图 5 输出侧U相电压 |
|
图 6 输出侧UV相线电压 |
|
图 7 输出侧三相电流 |
|
图 8 低调制比时中性点电压波动图 |
|
图 9 高调制比时中性点电压波动图 |
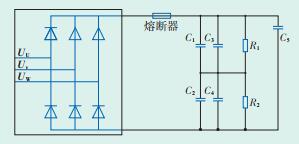
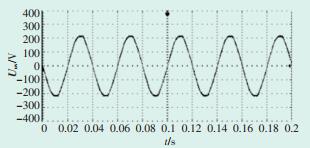
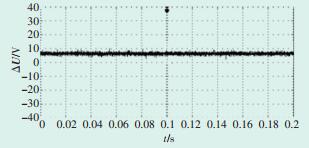
基于DSP TMS320F2812搭建二极管钳位型三电平逆变器实验平台,其主电路图如图 10所示。系统实验参数如下:电网电压U=380 V;系统运行仿真频率f=50 Hz;直流母线电压Udc=220 V;开关频率fs= 2000 Hz。图 11为线电压Uuv经滤波以后的波形,为正弦波;图 12为上、下电容电压差ΔU,其幅值在6 V左右且无偏移现象,基本实现了中点电压平衡。实验结果表明,本文所用算法可以满足预期要求。
|
图中:UU、UV、UW—分别为三相电压;C1、C2、C3、C4、C5—电容;R1、R2—电阻。 图 10 实验平台主电路图 |
|
图 11 线电压Uuv波形 |
|
图 12 上、下电容电压差 |
本文介绍了60°坐标系下SVPWM控制算法,采用坐标旋转变换的方法简化了大扇区判断及作用时间的计算,并在此基础上,加入中点电压平衡控制策略。仿真及实验验证了该算法的有效性。所采用的60°坐标系下SVPWM控制算法、坐标旋转变换方法及中点电压平衡控制策略可以推广到多电平逆变器SVPWM算法中。
| [1] |
Thomas Nathenas, Georgios Adamidis. A new approach for SVPWM of a three-level inverter-induction motor fed-neutral point balancing algorithm[J]. Simulation Modeling Practice and Theory, 2012(29): 1-17. |
| [2] |
Bhat A H, Langer N. Capacitor voltage balancing of three-phase neutral-point-clamped rectifier using modified reference vector[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 561-568. DOI:10.1109/TPEL.2013.2256930 |
| [3] |
邹萍萍.混合钳位型三电平半桥逆变器的研究[D].南京: 南京航空航天大学, 2013.
|
| [4] |
刘嫣. 一种改进的SVPWM算法研究[J]. 计算机仿真, 2010, 27(9): 328-332. |
| [5] |
雒浪, 吴杰康, 杨秀菊, 等. 新能源环境下配电网无功电压调节优化[J]. 广东电力, 2018, 31(6): 54-60. |
| [6] |
唐校, 杨向宇, 赵世伟. 基于60°; 坐标系的SVPWM过调制算法[J]. 华南理工大学学报(自然科学版), 2014, 42(8): 27-33. |
| [7] |
陈晓鸥, 许春雨, 王枫明. 60°; 坐标系下三电平逆变器SVPWM控制策略研究[J]. 电工电能新技术, 2017, 36(2): 43-49. |
| [8] |
孙强, 赵朝会, 詹俊, 等. 基于60°; 坐标系的两电平和NPC型三电平逆变器SVPWM算法研究[J]. 电机与控制应用, 2017, 44(6): 24-30. |
| [9] |
Bhat A H, Langer N. Capacitor voltage balancing of three-phase neutral-point-clamped rectifier using modified reference vector[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 561-568. DOI:10.1109/TPEL.2013.2256930 |
| [10] |
向超群, 陈春阳, 韩丁, 等. 中点电位不平衡度反馈的三、电平虚拟空间矢量调制方法[J]. 电机与控制学报, 2018, 22(3): 50-58. |
| [11] |
陈棋, 陈柬. 小信号分析在三电平ZVZCS充电桩中的应用[J]. 电力大数据, 2019, 20(1): 8-15. |
| [12] |
郜亚秋, 肖鹏, 张建, 等. 60°; 坐标系下三电平SVPWM算法和中点电压控制研究[J]. 电气传动自动化, 2015, 3(12): 12-16. |
| [13] |
李凯锋, 朱春毅, 邢卫宏, 等. 基于gh坐标系的三电平变频器SVPWM混合调制策略[J]. 电气技术, 2016, 35(9): 20-24. |
| [14] |
戚银.NPC三电平逆变器中点电位波动及共模电压协同抑制策略[D].天津: 天津大学, 2016.
|
 2020, Vol. 38
2020, Vol. 38