随着电力建设规模的迅速扩大,电网正逐步成为1个巨大的互联系统,使电力系统的计算机仿真变得特别复杂。尤其在进行电力系统电磁暂态仿真时,计算机的内存和计算速度往往达不到要求,而通过等值方法代替系统中与研究内容无关的部分(本文称“外部系统”),只保留需要研究的部分(本文称“研究系统”),即可大大减小仿真计算规模,节省运算时间[1-8]。
PSD(电力系统分析软件)中包含了全国电网绝大部分电气元件的实测数据,是目前进行电力系统外部等值计算最理想的数据源之一。PSD-SCCP(电力系统短路电流计算程序,以下简称SCCP)是PSD软件的1个子模块,可利用PSD计算文件对系统进行多端网络等值[9-10]。本文通过仿真方法对PSD-SCCP多端网络等值规律进行总结分析,对比基于和不基于潮流结果2种计算条件下等值参数的差异,并探讨2种计算条件下的等值适用范围。
1 SCCP多端网络等值规律PSD中包含了PSD-BPA(潮流及暂态稳定程序,以下简称BPA)、SCCP等众多子程序。SCCP程序的多点网络等值功能可根据DAT文件提供的电网拓扑结构及BPA的潮流计算结果,对系统进行多端口阻抗等值计算;可任意选择所要等值的节点(1000个以内),给出各节点对地的戴维南等值参数(理想电压源与等值阻抗串联)、诺顿等值参数(理想电流源与等值导纳并联),以及各节点之间的等值连接阻抗(包括正序、负序和零序参数)[11]。
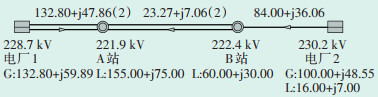
为了方便理解和验证SCCP程序的多点网络等值规律,在BPA中搭建了1个简单的两端电源系统进行仿真试验。系统由2个火电厂和2个220 kV变电站组成,该网络结构和潮流如图 1所示。
|
图 1 BPA电网结构及潮流图 |
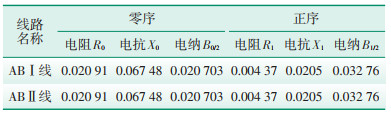
潮流计算的容量基准为100 MVA,220 kV系统的电压基准为230 kV。A站至B站双回线路正序和零序标幺值参数见表 1。
| 表 1 AB双回线路正序和零序标幺值参数 |
SCCP提供了2种等值条件,即基于潮流结果和不基于潮流结果,下面将母线A(A站220 kV母线)和母线B(B站220 kV母线)作为等值节点,分别对这2种条件下的等值参数进行仿真研究。
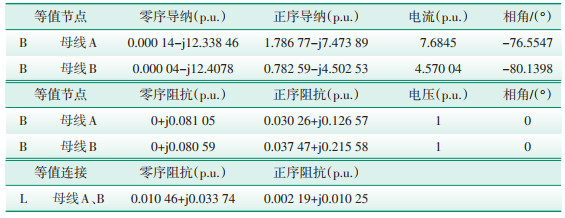
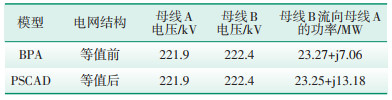
1.1 不基于潮流结果的等值计算在SCCP计算条件设置中不勾选基于潮流结果进行计算的选项,在图 1所示系统中选择母线A和母线B进行多端网络等值,等值结果见表 2。
| 表 2 不基于潮流结果的多端网络等值结果 |
从表 2看出,原系统被简化为母线A和母线B两个节点的诺顿等值形式或戴维南等值形式,同时,母线A和母线B之间还有1个等值连接阻抗。由于原网络母线A和母线B之间的电气连接只有AB双回线,据此推测,等值后母线A和母线B之间的等值连接阻抗即为AB双回线的等效阻抗。从表 1可算出,AB双回线的正序等效阻抗为0.002 19+j0.010 25,正好与等值后母线A和母线B之间的正序等值连接阻抗相等,零序亦如此,上述推测得到了验证。
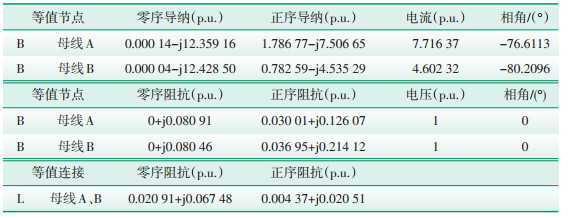
BPA用对称线路数据L卡模拟输电线路,L卡采用π型线路模型,线路并联导纳平均分成两部分分别并联于线路阻抗两端。从等值后的参数中找不到AB双回线的等效并联导纳参数,于是推测AB双回线两侧的并联导纳很可能被等值到了母线A和母线B的等值导纳参数中。为了验证此推测,在原BPA模型中删除AB二线后,再次利用SCCP对母线A和母线B进行网络等值,等值结果见表 3。
| 表 3 删除AB两线后的多端网络等值结果 |
对比表 3和表 2,表 3中母线A和母线B正序导纳比表 2减小了0.032 76,而此值正好等于AB二线的两侧并联导纳,零序亦如此,验证了上述推测。
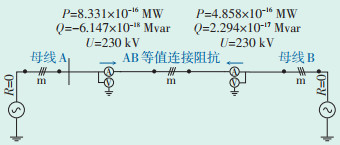
另外,上述等值是在不基于潮流结果的条件下进行的,因此母线A和母线B的戴维南等值电势幅值均为基准电压,两节点间无压差和相位差,两节点之间的功率应为0。在PSCAD中按照表 2数据搭建等值模型(见图 2)进行仿真验证,母线电压为基准电压,线路潮流为0,结果与原网络潮流不一致。
|
图 2 不基于潮流结果的PSCAD等值参数模型 |
通过上述分析,可得出如下结论:
(1)用SCCP进行多端网络等值后,原系统中等值节点之间的电气连接被等值为1个连接阻抗;
(2)原系统线路并联导纳会被等值到线路两侧节点的等值导纳中,或者说等值节点的导纳参数中包含了与其相连线路并联导纳的1/2;
(3)不基于潮流结果条件下的多端网络等值结果不能提供等值节点的电势幅值和角度,因此无法复现原网络潮流。
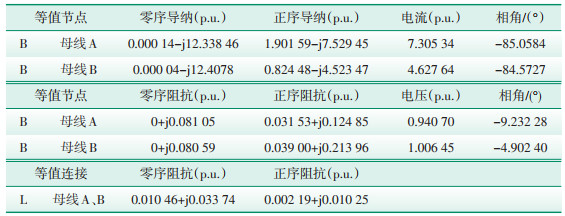
1.2 基于潮流结果的等值计算在SCCP仿真计算条件中勾选基于潮流结果进行计算,在图 1所示系统中选择母线A和母线B进行多端网络等值,等值结果见表 4。
| 表 4 基于潮流结果的多端网络等值结果 |
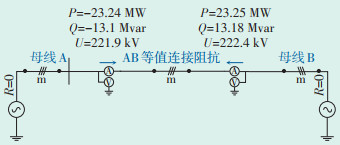
对比表 4与表 2,零序参数完全相同,等值连接阻抗参数完全相同,只有等值节点的正序导纳(阻抗)和电流(电势)参数不同。表 4中等值节点的电势幅值和角度不再是节点基准电压,而是基于潮流结果计算出来的;同理,等值节点的正序导纳(阻抗)参数也进行了一定程度的修正。基于表 4的等值参数重构的电网潮流应该与原网络潮流一致,否则基于潮流结果的等值条件就没有意义。下面在PSCAD中按照表 4搭建模型,验证PSCAD仿真结果是否与BPA潮流结果一致。PSCAD等值参数模型及仿真结果如图 3所示。
|
图 3 基于潮流结果的PSCAD等值参数模型 |
PSCAD与BPA潮流结果对比见表 5,母线电压和线路有功功率一致,但线路无功功率不一致,差值为6.12 Mvar。
| 表 5 PSCAD与BPA潮流结果对比 |
根据1.1节的结论,由于母线A和母线B等值节点导纳参数中包含了原系统中AB双回线的并联导纳,所以图 2所示PSCAD仿真中母线B流向母线A的潮流其实测量的是π型线路并联导纳线路阻抗侧的潮流,而图 1所示BPA仿真中母线B流向母线A的潮流其实测量的是π型线路并联导纳母线侧的潮流,两种潮流无功功率差值应为AB双回线在母线B侧的并联电纳产生的无功功率,下面通过数值计算进行验证。
AB单回线1/2对地电纳有名值为6.192 82×10-5 S,其在母线B电压为222.4 kV时的无功功率为3.06 Mvar,则AB双回线注入母线B的无功功率为6.12 Mvar,与表 5中等值前后线路无功功率差值相等,从而验证了上述论断正确。由此可见,表 3中2种模型仿真结果中母线B流向母线A的无功功率不一致是因测点不一致引起的,而事实上2种潮流结果是一致的。
需要特别指出的是,图 3模型中AB双回线是以等值连接阻抗形式出现的,若将AB等值连接阻抗替换为AB双回线,由于AB双回线的参数中有并联导纳,而母线A和母线B等值节点导纳参数中也包含了AB双回线的并联导纳,必然导致潮流结果与原系统不一致。可见,若将整个系统看做外部系统,则利用SCCP基于潮流结果对电网进行多点网络等值时,由等值参数重构的网络可复现原系统潮流;而若将AB双回线看做研究系统,其他部分看做外部系统,则利用SCCP基于潮流结果对外部系统进行网络等值时,由研究系统和等值参数重构的网络不能复现原系统潮流。
1.3 结论通过上述分析,可得出如下结论:
(1)电力系统潮流是基于正序参数计算得出的,与零序无关,因此是否基于潮流结果进行网络等值,对零序等值参数没有影响;
(2)基于潮流结果的网络等值条件只修正等值节点诺顿(戴维南)等值参数,对等值节点之间的连接阻抗参数没有影响;
(3)若将整个系统看做外部系统,则利用SCCP基于潮流结果对电网进行多点网络等值后,由等值参数重构的网络可复现原系统潮流。若将AB双回线看做研究系统,其他部分看做外部系统,则利用SCCP基于潮流结果对外部系统进行网络等值后,由研究系统和等值参数重构的网络不能复现原系统潮流。
2 适用范围基于上述结论,对SCCP多端网络等值适用范围总结如下。
(1)不基于潮流结果的多端网络等值可保留原系统的阻抗特性,但由于所有等值节点内电势相等,所以等值模型不能复现原系统潮流,适用于不关心系统潮流的仿真工作,如短路电流计算、特性阻抗分析等。
(2)基于潮流结果的多端网络等值可保留原系统的阻抗特性,等值模型可以复现原系统潮流,其适用范围在第(1)条的基础上可扩展到以系统潮流为基础的仿真领域,如电力系统潮流计算等。
(3)SCCP多端网络等值参数不能模拟原系统的动态特性,因此只适用于电力系统静态等值。
(4)SCCP多端网络等值的对象是整个系统,或者说SCCP将整个系统当作外部系统处理。若系统被划分为研究系统和外部系统,则无论是否基于潮流结果进行计算,SCCP均不适用于直接对外部系统进行网络等值。
3 结束语随着互联电网规模的不断扩大,开展电力系统等值方法的研究具有越来越重要的意义。本文利用仿真方法对PSD-SCCP多端网络等值规律进行了分析与总结,对比了基于潮流结果和不基于潮流结果2种计算条件下等值参数的差异,并对2种计算条件下的等值适用范围进行了探讨,研究结果可供相关人员开展电力系统仿真计算分析时参考。
| [1] |
文明浩, 杨帆. 基于PSASP短路计算的区域电网等值方法[J]. 电网技术, 2012, 36(1): 113-117. |
| [2] |
李明念, 杨秀. 基于PSASP短路计算的外网实用等值方法[J]. 电测与仪表, 2018, 55(16): 36-41. DOI:10.3969/j.issn.1001-1390.2018.16.007 |
| [3] |
刘宪林, 矫龙飞, 程子霞. PSASP动态等值功能的应用与分析[J]. 郑州大学学报(工学版), 2014, 35(1): 10-14. DOI:10.3969/j.issn.1671-6833.2014.01.003 |
| [4] |
林济铿, 闫贻鹏, 刘涛, 等. 电力系统电磁暂态仿真外部系统等值方法综述[J]. 电力系统自动化, 2012, 36(11): 108-115. |
| [5] |
朱琳, 葛俊, 吴学光, 等. 一种工程实用的电力系统等值方法[J]. 电力自动化设备, 2017, 37(9): 178-184. |
| [6] |
孙奇珍, 蔡泽祥, 朱林, 等. 互联电网的多端等值方法及其误差分析[J]. 电网技术, 2008, 32(23): 67-71. |
| [7] |
刘峰. 电力系统外部等值理论及实用化探讨[J]. 继电器, 2007, 35(15): 67-71. |
| [8] |
余娟, 张勉, 朱柳, 等. 考虑灵敏度一致性的外网静态等值新理论研究[J]. 中国电机工程学报, 2013, 33(10): 64-70. |
| [9] |
宫小宇, 吴集光, 曹斌, 等. 基于BPA-PSCAD软件500 kV输变电工程工频过电压的联合分析法[J]. 电瓷避雷器, 2017(6): 166-171. |
| [10] |
马志强. 网络等值与互联电网潮流分析[J]. 广东电力, 2004, 17(3): 71-74. DOI:10.3969/j.issn.1007-290X.2004.03.019 |
| [11] |
王虹富, 肖静, 张彦涛, 等.PSD-SCCP电力系统短路电流计算程序(2.5版)用户手册[Z].北京: 中国电力科学研究院, 2016.
|
 2020, Vol. 38
2020, Vol. 38