2. 国网内蒙古东部电力有限公司, 呼和浩特 010020
2. Eastern Inner Mongolia Electric Power Company Limited, Hohhot 010020, China
国内互联电网的发展非常迅速,大区振荡模式的阻尼也在不断改善,但对于主网末端的局部电网,由于交流联系薄弱,在远距离、大功率送电时仍存在低频振荡风险。低频振荡影响范围广、持续时间长,会对电网安全稳定运行造成巨大威胁[1-4]。
2017-07-01T06:44:00—07:12:00,中国东北某电网1台发电机发生了持续28 min的功率扰动,造成电厂送出线路以及区域电网与主网的联络线功率持续振荡,振荡频率约为1.25 Hz,属于低频振荡范围。该电网调度下令停运功率扰动机组后,电网功率振荡迅速平息。
根据以往电网多次发生的低频振荡事件,现有文献在其振荡机理、特性等方面已取得了许多重大成果[2-16]。机理方面,目前学术界和工程界普遍认为低频振荡可分为负阻尼振荡和强迫功率振荡。负阻尼振荡在采用现代快速、高顶值倍数励磁系统的条件下更容易发生,可通过电力系统稳定器(PSS)在弱阻尼或负阻尼频率附加阻尼解决。在强迫功率振荡理论研究方面,文献[4]指出了电力系统强迫功率振荡是由扰动频率接近系统固有振荡频率激起的谐振现象。文献[5]进一步分析了强迫功率振荡的主要影响因素,其振荡幅值与扰动的地点、幅值、系统惯量以及阻尼比的大小相关。还有部分学者从能量角度[6-7]和特征向量角度[8-9]对强迫功率振荡机理进行了研究分析。
在强迫功率振荡扰动源研究方面,有学者分别从原动机汽门调节功率[10-12]和负荷扰动方面[13]进行研究,也有学者研究了两者的不同机理,阐明了原动机功率与负荷持续周期性扰动造成电网功率振荡的区别[14]。文献[15]指出由发电机的轴系、励磁器、调速器等引起的周期性扰动都可能是振荡的起因。文献[16]提出一种判别强迫振荡与自由振荡的方法,指出采取针对性的控制措施可迅速消除振荡。
本文针对东北某电网振荡事件,分析其振荡原因,提出一种基于广域测量系统的外特性注入模拟低频振荡扰动源的时域仿真方法,利用综合稳定程序(PSASP)对该振荡事件进行仿真复现,根据小干扰分析出的系统固有振荡模式,分析了该电网强迫功率振荡风险对系统的影响,提出电网运行控制建议。
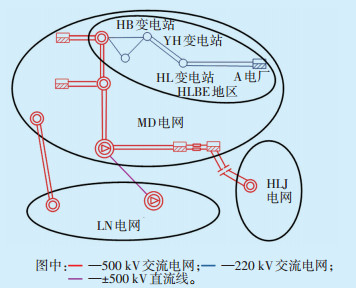
1 事件介绍 1.1 电网概况及事件过程图 1为东北某电网示意图。事件发生前HLBE地区全接线运行,与主网联网的HB变电站受电97 MW,地区负荷810 MW,发电总有功出力709 MW。HLBE地区220 kV网内共有3台200 MW火电机组运行,其中A电厂1号机组出力189 MW,2号机组出力191 MW,B电厂2号机组出力200 MW。110 kV及以下电网内火电机组出力56MW,风电出力44MW,光伏出力29 MW。
|
图 1 中国东北某电网示意图 |
2017-07-01T06:44:00,MD电网明显出现有功功率波动现象,网内A电厂1号机组功率异常波动,且噪音较大。06:52:00调度下令A电厂1号机组降低有功出力,提高励磁电流。07:01:00 A电厂汇报1号机有功出力、无功出力、励磁电流均无法调整,1号机组失控。07:08:00调度下令A电厂1号机组解列。07:12:00随着A电厂1号机组打闸停机,网内潮流波动迅速消失。
1.2 事件原因调查发现,由于A电厂1号发电机出口W相电流变送器烧损,并且该变送器的交流电源火线与电流输入端零线燃烧黏接在一起,导致交流电源串入发电机出口第4组电流互感器二次回路,造成机组数字电调系统(Digital Electric Hydraulic control System,DEH)功率采集用的2块有功功率变送器测量值持续过高,使机组负荷高限保护以约1.25 Hz为周期关、开调速汽门,持续动作引起机组功率周期性波动,属于典型的低频振荡故障。
2 故障反演故障发生后,相关生产运行部门迅速组织专业人员对故障过程进行仿真分析,验证电网仿真计算模型参数的准确性。
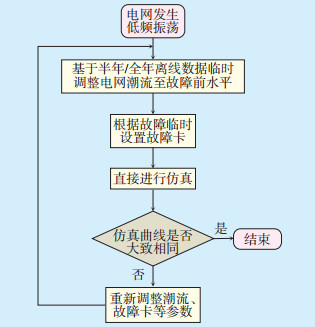
2.1 故障反演传统方法传统的故障反演方法用时较长,仅在潮流准备阶段,从收集故障前各项电网运行状态的数据到调整完仿真数据就需要1至2周的时间,低频振荡故障反演所需时间更长。传统故障反演通过负荷冲击、快速调节汽门、发电机跟踪调节等方法对故障扰动进行模拟,该方法只能拟合出故障过程中电网的大致趋势,故障模拟方法不仅复杂,需要耗费大量时间对故障扰动特征进行拟合,而且对仿真准确性的干扰因素非常多,只能对故障反演结果进行定性分析。图 2所示为传统低频振荡故障反演流程。
|
图 2 传统低频振荡故障反演流程示意图 |
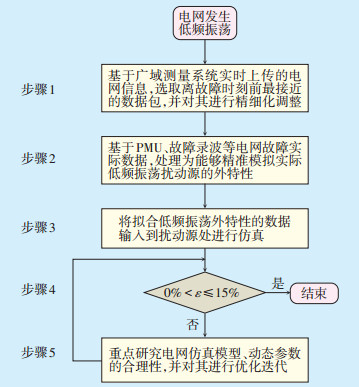
本文提出一种基于广域测量系统的外特性注入模拟低频振荡扰动源的时域仿真方法,通过广域测量系统可以快速生成接近故障时刻的电网潮流数据,大幅缩短故障反演所需时间。利用向量测量单元(PMU)、故障录波等电网实际数据,能够精准模拟生成实际低频振荡扰动源的外特性数据,代替传统方法中设置故障卡的步骤,再将数据输入时域仿真系统,完成低频振荡事故时域仿真反演。为保证时域仿真结果的合理性,引入误差范围表征参数ε,定量分析电网实际结果与仿真结果的误差范围。考虑到仿真结果应服务于实际运行,在不能过于保守的基础上留有一定裕度,综合得出ε∈(0%,15%]比较合理。改进后的反演方法有效降低了因仿真基础潮流、低频振荡扰动与实际电网事故设计不合理造成的差异,提高了故障反演流程的灵活性、准确性与可靠性。改进后的低频振荡故障反演流程见图 3所示。
|
图 3 改进后的低频振荡故障反演流程示意图 |
改进方法的步骤1和步骤2基本可以保证稳态潮流和低频振荡扰动的准确性;若ε不在要求的范围内,则应重点研究电网时域仿真模型和动态参数的合理性,对其进行优化迭代分析,见公式(1)。
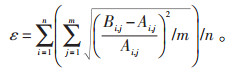
|
(1) |
其中,i=1,2,3,…,n;n 为低频振荡近区关键电厂、线路、主变压器个数;j=1,2,3,…,m;m为仿真过程中低频振荡的周期个数;Ai, j为第i 个设备中第j 个周期的电网实际振荡幅值;Bi, j为第i 个设备中第j 个周期的时域仿真振荡幅值(功率、电压、功角等参数)。
3 仿真结果采用改进后的低频振荡故障反演方法,在发电机主变压器高压侧上施加与振荡期间完全一致的周期性功率扰动,以保证故障反演结果的准确性。
根据故障录波显示,电网振荡期间A电厂1号机以1.25 Hz为振荡频率,其中有功功率的最大振荡幅值为125 MW(波峰到波谷距离的一半),无功振荡幅值较小,主变压器高压侧有功功率振荡曲线如图 4所示。
|
图 4 A电厂G1主变压器高压侧有功功率振荡曲线 |
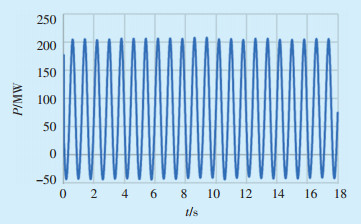
HLBE电网通过500 kV HB变压器与主电网相连,仿真表明HB变压器受电有功功率录波曲线在0~390 MW波动,与实测曲线在20~360 MW波动基本相符。两者在前几次振荡时差别较大,因为实测曲线取于振动过程中,而仿真曲线则选取在振荡开始阶段。强迫功率振荡起振快,振荡在第3个振荡周期就接近最大幅值,如图 5所示。
|
图 5 HB变电站受电有功功率录波实测曲线与仿真曲线比较 |
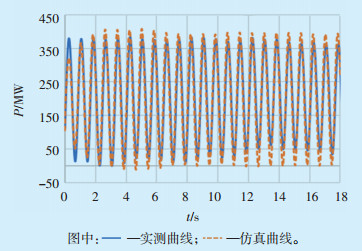
A电厂近区YH-HL变电站断面有功功率录波仿真曲线在受电110 MW至外送280 MW间波动,实测曲线在受电110 MW至外送260 MW间波动,两者基本相符,如图 6所示。
|
图 6 YH-HL变电站断面有功功率录波实测曲线与仿真曲线比较 |
通过对A电厂送出线路及关键主变压器数据进行量化计算分析可知ε=7.04%,满足指标要求,能较好的重现本次由电厂强迫振荡引起的系统波动情况,验证了低频振荡故障反演改进方法的有效性及该电网运行方式计算仿真模型参数的准确性。
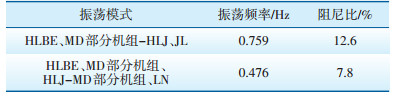
4 风险分析在扰动频率为1.25 Hz的电网振荡期间,虽然电网无负荷损失,且频率及电压均无越限,但根据电力系统强迫功率振荡原理,当扰动频率接近系统固有振荡频率时,会引起系统谐振,导致电网振荡幅值增大,给电网安全稳定运行带来威胁。为验证强迫功率振荡可能对该电网造成的风险,经分析得到HLBE地区电厂机组及电网的系统固有振荡模式有2种,见表 1所示。
| 表 1 小干扰分析结果 |
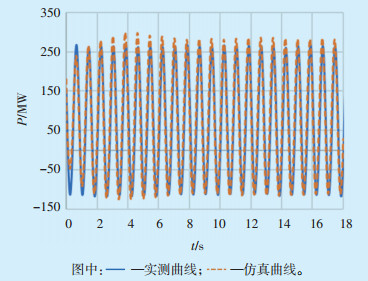
以阻尼比较强的HLBE地区与MD电网部分机组相对HLJ、JL机组振荡模式为例,将A电厂扰动频率由1.25 Hz改为0.759 Hz,振荡幅值及其余边界条件不变。仿真结果见图 7—图 9。
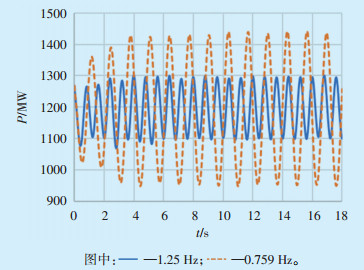
|
图 7 MD-HLJ断面有功功率曲线 |
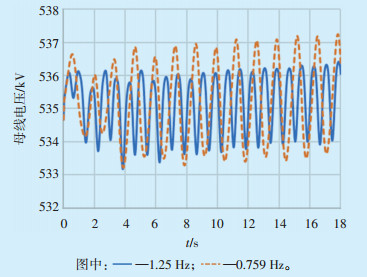
|
图 8 MD-HLJ断面近区500 kV母线电压曲线 |
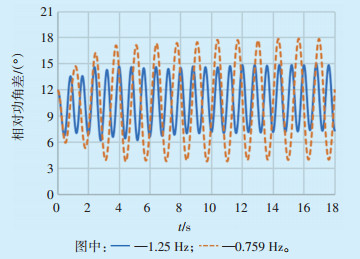
|
图 9 MD-B电厂相对HLJ-C电厂功角曲线 |
可见,修改A电厂1号机扰动频率后,MD-HLJ断面有功功率比修改前起振幅度增大,稳态最大振荡幅值由100 MW增大到250 MW。说明当强迫功率振荡频率接近系统固有振荡频率时,系统谐振导致固有振荡模式区域间有功功率振荡增大是破坏系统稳定性的主要因素。而近区电压及两区域相对功角差幅值虽然有所增大,但因振幅基数小,故不是破坏系统稳定性的主要因素。
对振荡频率为0.476 Hz的HLBE、MD部分机组、HLJ机组相对MD部分机组、LN机组振荡模式进行机仿真校核,结论与振荡频率为0.759 Hz模式相同。结果表明:将扰动频率修改到系统固有振荡频率后,虽然联络线有功功率振荡并未导致系统失稳,但若扰动源幅值过大且不能及时得到处理,电网将长时间处于该强迫功率振荡模式,在某些恶劣条件下,振荡可能会引起其他连锁反应,影响电网安全稳定运行。
5 结论通过改进低频振荡故障反演方法,复现了某省级电网振荡事件,并分析了电网可能存在的风险,得出以下结论。
(1)改进后的电力系统强迫功率振荡故障反演方法,利用广域测量系统大幅缩短调整故障前时刻电网潮流数据的时间,并简化强迫功率振荡扰动源的模拟,有效提高了故障反演流程的灵活性、准确性与可靠性。
(2)利用时域仿真方法复现了本次振荡事件,证实了本次振荡事件属于强迫功率振荡及该电网运行方式计算仿真模型参数的准确性。
(3)通过小干扰分析,HLBE电网存在频率约为0.759 Hz和0.476 Hz的系统固有振荡频率。由于周期性扰动是强迫功率振荡的必要条件,建议加强对电厂相关扰动源的管理,特别是与HLBE电网固有振荡频率相近的扰动,避免类似事件再次发生。
(4)强迫功率振荡期间,薄弱断面功率可能会超过其静稳极限,对电网安全稳定运行造成威胁。应提高薄弱断面静稳极限,并在实际电网运行中留有充足裕度。
| [1] |
倪以信. 动态电力系统理论与分析[M]. 北京: 清华大学出版社, 2002.
|
| [2] |
李丹, 苏为民, 张晶, 等. "9.1"内蒙古西部电网振荡的仿真研究[J]. 电网技术, 2006, 30(6): 41-47. DOI:10.3321/j.issn:1000-3673.2006.06.008 |
| [3] |
顾丽鸿, 周孝信, 陶洪铸, 等. 局部弱联诱发互联电网强迫振荡机制分析[J]. 电网技术, 2010, 34(12): 36-43. |
| [4] |
李兆伟, 方勇杰, 李威, 等. 电力系统强迫功率振荡研究综述[J]. 华东电力, 2013, 41(6): 1188-1193. |
| [5] |
汤涌. 电力系统强迫功率振荡的基础理论[J]. 电网技术, 2006, 30(10): 29-33. DOI:10.3321/j.issn:1000-3673.2006.10.006 |
| [6] |
韩志勇, 贺仁睦, 徐衍会, 等. 基于能量角度的共振机理电力系统低频振荡分析[J]. 电网技术, 2007, 31(8): 13-16. DOI:10.3321/j.issn:1000-3673.2007.08.003 |
| [7] |
余一平, 闵勇, 陈磊, 等. 基于能量函数的强迫功率振荡扰动源定位[J]. 电力系统自动化, 2010, 34(5): 1-6. |
| [8] |
苗友忠, 汤涌, 李丹, 等. 局部振荡引起区间大功率振荡的机理[J]. 中国电机工程学报, 2007, 27(10): 73-77. DOI:10.3321/j.issn:0258-8013.2007.10.012 |
| [9] |
马燕峰, 赵培龙, 赵书强. 多机电力系统的强迫功率振荡特性研究[J]. 电力系统保护与控制, 2013, 41(24): 23-29. DOI:10.7667/j.issn.1674-3415.2013.24.004 |
| [10] |
余一平, 闵勇, 陈磊. 多机电力系统强迫功率振荡稳态响应特性分析[J]. 电力系统自动化, 2009, 33(22): 5-9. |
| [11] |
徐衍会, 贺仁睦, 韩志勇. 电力系统共振机理低频振荡扰动源分析[J]. 中国电机工程学报, 2007, 27(17): 83-87. DOI:10.3321/j.issn:0258-8013.2007.17.016 |
| [12] |
韩志勇, 贺仁睦, 徐衍会. 由汽轮机压力脉动引发的电力系统共振机理低频振荡[J]. 中国电机工程学报, 2005, 25(21): 14-18. DOI:10.3321/j.issn:0258-8013.2005.21.003 |
| [13] |
余一平, 闵勇, 陈磊, 等. 周期性负荷扰动引发强迫功率振荡分析[J]. 电力系统自动化, 2010, 34(6): 7-11. |
| [14] |
韩志勇, 贺仁睦, 马进, 等. 电力系统强迫功率振荡扰动源的对比分析[J]. 电力系统自动化, 2009, 33(3): 16-19. DOI:10.3321/j.issn:1000-1026.2009.03.003 |
| [15] |
王铁强, 贺仁睦, 王卫国, 等. 电力系统低频振荡机理的研究[J]. 中国电机工程学报, 2002, 22(2): 21-25. DOI:10.3321/j.issn:0258-8013.2002.02.005 |
| [16] |
叶华, 宋佑斌, 刘玉田. 强迫功率振荡响应解析与振荡类型判别[J]. 中国电机工程学报, 2013, 33(34): 197-204. |
 2019, Vol. 37
2019, Vol. 37