近年来,分布式发电(Distributed Generation,DG)应用范围及规模不断扩大,DG并网可缓解用电压力,有效改善配电网的电能质量、提高供电可靠性[1-2]。然而,以光伏、风电为典型代表的新能源,出力具有间歇性、随机性,波动较为明显等特点。高渗透率的DG并网必然会给配电网的安全稳定运行带来一定压力,引起电压越限、电压波动等问题[3-4]。为了应对大规模DG并网带来的问题,分布式储能系统(Distributed Energy Storage System)适时而生[5-6]。储能装置可以平抑DG出力波动,减小含DG的配电网电压越限风险[7-8],通过合理配置储能可以提高配电网对DG消纳能力。
目前,配电网中分布式储能的优化配置问题已受到各领域的广泛关注。文献[9]基于价格型需求侧响应的不确定性,建立了基于模糊机会约束规划的并网型光伏微电网储能系统优化配置模型,通过对模糊机会约束的清晰等价处理,将模糊机会优化问题转换为确定性的优化问题进行求解。文献[10]以最小化分布式储能安装成本与敏感负荷的电压越限成本为目标,建立了分布式储能与电压动态补偿器联合的控制模型,然后基于蚁群算法求解储能系统的最优容量配置。文献[11]从储能投资者利益出发, 兼顾系统运行经济性,建立了以储能投资成本、线损费用、购电费用最小为目标的上层优化模型,并引入层次分析法将该多目标优化问题转化为单目标问题;将储能配置与其运行调度相结合,建立了以负荷标准差最小为目标的下层储能运行策略优化模型。文献[12-13]结合峰谷电价政策,以最大化年效益和DG消纳率最大为目标,构建了工业光储系统的储能容量优化配置方法。文献[14]建立了混合储能系统优化配置模型,用于平抑风电场功率波动,结合改进遗传算法提出了一种混合储能系统优化配置方法。文献[15]以光伏利用率最大和年净利润最大为目标,构建了工业光伏微电网的储能容量优化配置的多目标优化模型,并将所提方法应用于广东某实际工业光伏微电网中,使得经过优化的储能系统可在离网情况下保证系统中重要负荷的稳定运行,在并网运行时促进光伏的就地消纳。
如上所述,目前大部分研究工作主要是利用储能与DG的协调优化调度实现配电网的经济运行,而通过储能配置来提高电网对高渗透率DG的消纳水平,提高电网运行安全性的研究较少。本文首次提出DG接入配电网耐受渗透比概念,并作为评价指标来衡量配电网对DG的消纳能力;为平抑DG出力波动幅度,提出了基于DG出力峰值削减的储能充放电控制策略,通过分析储能配置比与耐受渗透比提高幅度之间的灵敏度关系,进而提出考虑耐受渗透比的分布式储能优化配置方法;通过仿真分析,表明通过合理配置分布式储能容量可以提高配电网DG消纳水平。
1 DG接入配电网的耐受渗透比 1.1 耐受渗透比定义配电网DG规划中,通常以DG安装容量来衡量配电网DG消纳能力[16]。配电线路合理的DG安装容量,与配电线路的负荷情况、配变总容量、线径、线路长度、首端母线电压、DG安装位置等众多因素相关。各条实际配电线路的物理参数和运行状态存在很大差异,进行DG规划时需要针对特定线路,获取详细的线路参数信息,进行建模求解,规划过程十分复杂困难。
为了得到具有普适性和工程实用性的DG规划方法,考虑到配电网的配电变压器总容量和线路直径一般是按照配电线路的额定容量成比例进行设计和建设的,本文提出耐受渗透比(Tolerant Permeability Ratio)概念。
耐受渗透比TPR是指满足电压和电流的安全性约束下,配电线路能够承受的最大DG渗透比,即不造成电压越限和电流过载的最大渗透比值,见式(1):
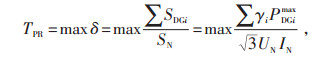
|
(1) |
式中 δ—配电线路的渗透比;
SN—配电变压器总容量;
SDGi—第i个DG的装机容量;
γi—第i个DG容量虚高系数;
PDGimax —第i个DG的峰值出力;
UN、IN—配电线路额定电压、额定电流。
考虑到日照条件、灰尘遮挡、衰减损耗等因素的影响,光伏的实际出力很难达到峰值功率[17]。通常情况下,光伏的实际最大出力与光伏装机容量的比值可以近似取为85%,容量虚高系数γ=1.18。
耐受渗透比计算应满足一定的约束条件,具体而言该约束条件为安全性约束(硬约束),即保证配电网的节点电压不越限以及线路电流不过载[18],如式(2)所示:
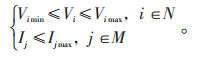
|
(2) |
其中,Vimin为节点电压下限,Vimax为节点电压上限,Ijmax为支路载流量上限,N为配电网节点数,M为配电网支路数。
耐受渗透比取电压和电流约束下的最小值,采用耐受渗透比评价指标来衡量配电网DG消纳能力,涵盖了配电线路配变总容量和线路直径的影响,更加简明直观,具有通用性。
1.2 DG耐受渗透比提高幅度指标当配电线路中实际或预期DG渗透比大于安全约束下线路的耐受渗透比(不考虑储能配置时的配电线路耐受渗透比)TPR0时,即δ>TPR0,为了表示DG渗透比超过线路耐受渗透比的程度,定义线路DG渗透比越限度LTPR,其计算公式如式(3):

|
(3) |
当实际或规划中配电线路的DG渗透比越限度LTPR大于0时,为了保证系统的安全稳定运行,可以考虑在DG并网点配置一定容量的储能装置,通过控制储能的充放电功率来削减DG出力峰值,从而提高线路对DG的消纳能力,即通过配置储能提高线路的耐受渗透比,为了表示储能配置前、后线路耐受渗透比的变化情况,定义线路耐受渗透比提高幅度指标λTPR,见式(4):
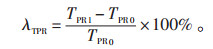
|
(4) |
其中,TPR1为考虑储能配置后的配电网耐受渗透比。
根据DG渗透比越限度LTPR和线路耐受渗透比提高幅度λTPR的定义可知,当LTPR>0时,为了保证配电线路对DG的消纳能力,可以配置一定容量的储能,使得λTPR=LTPR,即可避免因DG渗透比过高而引起的安全问题。
2 考虑DG出力峰值削减的储能充放电优化控制策略对于间歇性DG,其一天内的出力往往随天气的变化呈现较大的波动性和峰谷差,而配电网对DG的消纳能力主要和DG的出力峰值相关[19],因此为了在不改变网架结构以及不引起弃光弃风的前提下,提高配电网的DG消纳能力,需要在DG侧配置一定容量的储能,并制定考虑DG出力峰值削减的储能充放电优化控制策略,该策略以减小全天DG和储能联合出力的峰谷差为目标,在考虑储能最大充放电功率和容量限制的前提下,通过控制储能在一天中各时段的充放电功率,实现DG注入系统有功功率峰值的削减。相应的策略模型如下。
2.1 目标函数优化目标函数为风储或光储联合出力的方差最小。方差越大,风储或光储联合出力的峰谷差越大,联合出力曲线越不平坦;方差越小,风储或光储联合出力的峰谷差越小,联合出力曲线越平坦。优化目标函数见式(5):
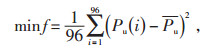
|
(5) |
式中 Pu(i)—第i个优化时段风储或光储联合出力值,即:
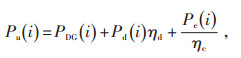
|
(6) |
风储或光储联合出力的平均值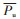
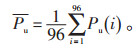
|
(7) |
其中,PDG(i)为第i个时段DG的出力;ηc为蓄电池充电效率;ηd为蓄电池放电效率。
2.2 优化变量优化周期一般取为1 d,优化时间间隔为15 min,则1 d有96个优化时段。优化变量为蓄电池在1 d中各时段的充电功率Pc和放电功率Pd,放电时功率为正值,充电时功率为负值。
2.2.1 约束条件 2.2.1.1 储能装置输出功率约束蓄电池第i个时段输出的有功功率受蓄电池最大充放电功率的限制,即:
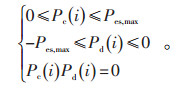
|
(8) |
式中 Pes, max—储能装置最大的充放电功率,即额定功率。
2.2.1.2 蓄电池充放电平衡蓄电池运行过程中的荷电状态(state of charge, SOC)存在上下限,当蓄电池的荷电状态值SOC达到上下限时,储能装置退出运行[20]。因此每个优化时段后蓄电池的SOC应在允许的上下限之间。

|
(9) |
其中,SOCmax、SOCmin分别为蓄电池荷电状态的上下限,SOC(i)为第i个优化时段后,蓄电池的荷电状态,表达式见式(10):
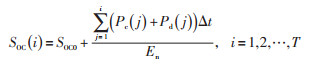
|
(10) |
其中,SOC0为蓄电池初始荷电状态;En为储能装置额定容量。
由于蓄电池储能系统对削峰填谷的目标即为将1 d的风储或光储出力峰谷差减为最小;同时,需保证蓄电池储能系统在第二天及以后能持续正常工作(不考虑蓄电池储能系统故障、检修等情况),就必须对蓄电池的剩余容量加以限制,即在1个充放电周期(24 h)内蓄电池的充电和放电总量应相等,即:

|
(11) |
本文以DG装机容量为基准容量,储能配置比αes定义为储能装置的极限功率与DG装机容量的比值,计算公式见式(12):
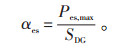
|
(12) |
为了提高含有高渗透率DG的配电网运行的安全可靠性,DG与储能的协调互补规划是一项重要的基础性工作。特别当配电网DG渗透比大于配电网耐受渗透比时,可能会出现电压越限和电流过载的风险,此时应考虑配置储能,提高配电网对DG的消纳能力,保证配电网安全稳定运行。当配电网实际接入或预期接入DG的渗透比高于配电网的耐受渗透比,配电网可能出现电压越限和电流过载的安全问题,需要配置储能削减DG出力的峰谷差,配电网可以接纳更多容量的DG,等效地提高了配电网的耐受渗透比。
3.2 优化步骤通过上文分析,可以按照以下步骤对DG接入配电网的储能进行优化配置。
(1)获取配电网的耐受渗透比TPR0;
(2)根据配电线路额定容量和实际接入或预期接入DG容量SDG,计算实际或预期渗透比δ、DG渗透比越限度LTPR;
(3)若LTPR=0,则无需配置储能,否则,执行步骤(4);
(4)计及各种天气出现的概率,计算配电线路耐受渗透比提高幅度最大值λTPRm;
(5)计算储能配置比αes相对于耐受渗透比提高幅度λTPR的灵敏度Spv(物理意义为:耐受渗透比提高单位幅度需要增加的储能配置比);
(6)计算储能配置比αes。若LTPR>λTPRm,则配置足够量的储能后系统仍存在一定的安全风险,此时储能的配置比αes为:

|
(13) |
若LTPR≤λTPRm,则配置一定量的储能后能够避免系统出现安全风险,此时储能的配置比αes为:

|
(14) |
(7)根据αes计算配置储能的额定功率PN和容量EN。

|
(15) |
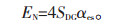
|
(16) |
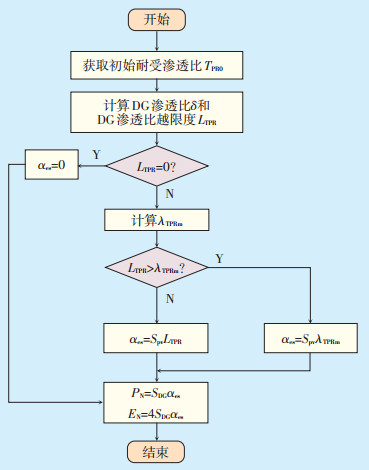
DG接入配电网的储能优化配置流程如图 1所示。
|
图 1 考虑耐受渗透比的分布式储能优化配置流程 |
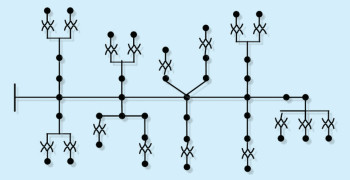
南方地区某条含DG的实际架空配电线路的拓扑结构如图 2所示,线路长度为5.8 km,平均负载率33%,平均母线电压10.3 kV,平均功率因数0.93,额定容量7.3 MVA,预期光伏总装机容量6 MW。原始耐受渗透比TPR0=0.64,储能容量与储能极限功率按4 :1的比例进行配置。
|
图 2 含DG架空配电线路拓扑结构 |
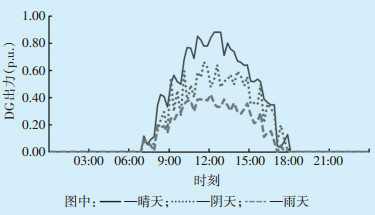
晴天、阴天和雨天天气情况下,光伏的典型日出力曲线如图 3所示。其中该地区晴天、阴天和雨天3种天气情况出现的概率分别为14.3%、42.7%和43.0%。
|
图 3 3种天气情况下光伏日出力曲线 |
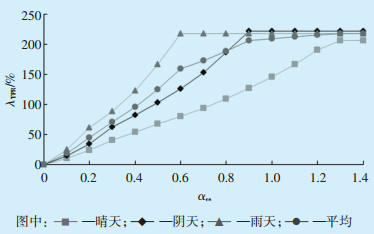
基于上述储能充放电优化控制策略,考虑3种天气情况,储能配置比αes从0~1.4变化,步长为0.1,得到DG接入的配电网耐受渗透比提高幅度λTPR,并计及各种天气出现的概率,计算出耐受渗透比提高幅度λTPR的曲线如图 4所示。
|
图 4 耐受渗透比提高幅度 |
由图 4可知,随着αes的增加,λTPR先增加后趋于稳定。这是因为当储能配置比达到一定大小,优化后光储联合出力为恒定值(即光储联合出力曲线近似为水平的直线),此时再增加配置储能,耐受渗透比提高幅度也趋于稳定,将此状态下的储能配置比称为饱和储能配置比。其中当系统中储能配置比达到饱和储能配置比(0.9)时,λTPR趋于稳定且达到最大值λTPRm=207%。
在计及各种天气出现概率的基础上,以λTPR为横坐标,αes为纵坐标,绘制二者的关系曲线并进行拟合,可以得到αes与λTPR的函数关系,如图 5所示。

|
图 5 耐受渗透比提高幅度和储能配置比的关系 |
当λTPR小于207%时,αes与λTPR具有比较明显的线性关系,进行线性拟合,相关系数R2=0.99,拟合的线性函数为:y=0.41x,x<2.07。
当λTPR大于207%时,随着αes的增加,λTPR几乎不变。
因此,在一定误差范围内,αes与λTPR的关系函数为:
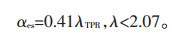
|
随着储能配置比的增加,耐受渗透比先增加后趋于稳定,耐受渗透比提高幅度存在最大值λTPRm= 207%。当耐受渗透比提高幅度小于207%(储能配置比例小于0.9),储能配置比αes相对于耐受渗透比提高幅度λTPR的灵敏度Spv为:
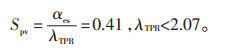
|
由上述的分析可得到,对于接入DG的配电系统,αes与λTPR之间存在明显的线性函数关系。
4.2 仿真验证为验证本文所提方法的有效性,基于上述储能的优化配置模型,制定了不配置储能、配置50%的储能容量、配置最优储能容量3种方案(以下简写为方案1、方案2、方案3),储能配置如表 1所示,分别进行潮流仿真,进而统计出各方案的电压越限概率,如表 2所示。
| 表 1 储能配置的3种方案 |
| 表 2 3种方案的电压越限概率 |
由统计数据可知,方案1由于没有配置储能,不能通过储能充放电削减DG峰值出力,导致电压越限概率最高;方案2配置了50%的储能容量,通过储能充放电削减了DG峰值出力,将系统的耐受渗透比由原来的0.64提高到0.72,但在个别时段仍会出现电压越限现象;而方案3的储能配置能够合理的消纳DG峰值出力,等效提高系统的耐受渗透至预期的渗透比,从而有效抑制电压越限。
实际算例表明,本文所提的储能优化配置方法可以有效地提高配电网DG消纳水平,保证系统稳定运行。
5 结束语分布式储能并网是配电网发展的必然趋势,通过合理配置储能提高配电网DG消纳水平已成为当前配电网的1个重要研究课题。高渗透率DG接入配电网可能存在功率倒送和电压越限问题,而通过在DG侧配置储能装置,可以改善出力特性,提高配电网对DG消纳能力。本文提出的基于DG出力峰值削减的储能充放电优化模型,以及DG接入配电网的储能优化配置方法,可供开展配电网储能配置研究工作参考。
| [1] |
张静炜, 朱想, 赫卫国, 等. 考虑光伏发电和储能系统调压能力的配电网储能容量优化配置[J]. 广东电力, 2018, 31(7): 30-35. |
| [2] |
杨年杰.分布式光伏并网对配电网电能质量的影响及对策研究[D].广州: 广东工业大学, 2018.
|
| [3] |
赵琦, 管霖, 吕耀棠, 等. 储能电站在含光伏电源配电网中的优化配置[J]. 广东电力, 2018, 31(7): 1-7. |
| [4] |
柴园园, 郭力, 王成山, 等. 含高渗透率光伏的配电网分布式电压控制[J]. 电网技术, 2018, 42(3): 738-746. |
| [5] |
陈深, 毛晓明, 房敏, 等. 微电网中储能技术研究进展与展望[J]. 广东电力, 2014, 27(2): 11-16. DOI:10.3969/j.issn.1007-290X.2014.02.003 |
| [6] |
Toledo O M, Oliveira Filho D. Distributed photovoltaic generation and energy storage systems:A review[J]. Renewable & Sustainable Energy Reviews, 2010, 14(1): 506-511. |
| [7] |
宁阳天, 李相俊, 董德华, 等. 储能系统平抑风光发电出力波动的研究方法综述[J]. 供用电, 2017, 34(4): 2-11. |
| [8] |
靳雯皓, 刘继春, 刘俊勇. 平抑风电功率波动的新型储能系统控制策略[J]. 电测与仪表, 2018(24): 78-87. DOI:10.3969/j.issn.1001-1390.2018.24.014 |
| [9] |
李姚旺, 苗世洪, 刘君瑶, 等. 考虑需求响应不确定性的光伏微电网储能系统优化配置[J]. 电力系统保护与控制, 2018(20): 69-77. DOI:10.7667/PSPC171431 |
| [10] |
马兴, 李俊杰, 黎博, 等. 分布式储能参与电压暂降补偿的优化配置与控制策略[J]. 郑州大学学报(工学版), 2019, 40(3): 1-8. |
| [11] |
陈厚合, 刘丽娜, 姜涛, 等. 提升配电网电压质量的分布式储能经济优化配置方法[J]. 电网技术, 2018, 42(7): 2127-2135. |
| [12] |
许健.工业用户型光伏微电网的电池储能系统优化配置方法[D].北京: 华北电力大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-11412-1016272045.htm
|
| [13] |
茆美琴, 金鹏, 张榴晨, 等. 工业用光伏微网运行策略优化与经济性分析[J]. 电工技术学报, 2014, 29(2): 35-45. DOI:10.3969/j.issn.1000-6753.2014.02.004 |
| [14] |
江润洲, 邱晓燕, 陈光堂. 风电场混合储能系统优化配置方法[J]. 电力系统及其自动化学报, 2015, 27(1): 37-42, 48. DOI:10.3969/j.issn.1003-8930.2015.01.007 |
| [15] |
许健, 刘念, 于雷, 等. 计及重要负荷的工业光伏微电网储能优化配置[J]. 电力系统保护与控制, 2016, 44(9): 29-37. |
| [16] |
张勇军, 林晓明, 张紫珩, 等. 基于耐受渗透比的10 kV配电网分布式电源规划[J]. 电力系统保护与控制, 2018, 46(9): 49-54. |
| [17] |
张紫珩.低压配电网模型及光伏配置应用策略研究[D].广州: 华南理工大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10561-1018875168.htm
|
| [18] |
杨雨瑶.分布式光伏接入配电网极限容量评估和拓展无功优化研究[D].广州: 华南理工大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10561-1017733531.htm
|
| [19] |
李宏仲, 高宇男, 张雪莹, 等. 地区电网光伏消纳能力的提升策略[J]. 电力自动化设备, 2018, 38(7): 114-120, 127. |
| [20] |
张欣.二阶锥优化在含风电接入的配电网储能规划双层模型中的研究应用[D].西安: 西安理工大学, 2018.
|
 2019, Vol. 37
2019, Vol. 37 


