2. 国网湖南省电力有限公司经济技术研究院, 长沙 410000
2. Hunan Inst. of Electric Power Corporation Economic & Technology, Changsha 410000, China
负荷预测是电力规划的基础,对指导电网建设、安排运行方式有着重要意义。影响地区负荷特性的因素众多,如经济、气温、电力消费结构等,还包含许多不确定性因素[1-3],导致预测精度达不到理想要求。随着电力需求总量的增加,中长期负荷预测备受广大学者的关注。
目前,工程中应用较多的方法是时间序列法[4]。该方法基于历史负荷进行趋势外推,具有直观、简便的特点;但由于在预测过程中缺乏专家参与,对不确定因素考虑不足,使得结果难以令人满意。文献[5]提出一种兼顾城市化因素的预测模型,解决了不确定性因子给预测带来的困难。基于D-S证据理论的预测模型能够与专家经验较好地融合[6-7]。此外,人工神经网络、灰色模型等智能算法相继应用于中长期负荷预测[8-16]。现有方法的不足主要体现在以下两个方面:一是模型的物理意义不够明晰,使得参数配置过分依赖于复杂的算法,工程应用性不强;二是模型与负荷的影响因素之间没有构建直观的解析关系,使得事后无法找出预测偏差的根源,因此难以指导预测结果的修订。
为解决上述问题,本文提出了一种新的预测模型及参数配置方法。首先,提出了一种新的负荷组合方案,即总负荷由基础负荷、气象负荷和不确定性负荷3部分组成。其次,深入分析了3类因素对电力需求的影响。然后,采用回归分析建立了基础负荷与GDP的非线性关系,以及气象负荷之于居民消费和极端气温持续时间、不确定性负荷之于大用户用电的线性关系,并将3类负荷相组合,提出多因素模型(Multi-Factor Model,MFM);基于最小二乘法原理提出了a、b、c参数的计算公式。最后,实例验证本文方法的有效性。
1 负荷分解与组合 1.1 负荷分解电力负荷具有较强的季节性。文献[17]将负荷分解成2部分:
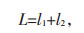
|
(1) |
式中 L—总负荷;
l1—基础负荷,主要受经济因素影响;
l2—气象负荷,夏季称为降温负荷,冬季称为取暖负荷。
影响l2的主要因素为极端气温持续时间;另外,由于居民消费水平的提高,地区空调、取暖桌等季节性电器保有量增加,对拉动l2亦起到一定的积极作用。
常用的负荷分离方法有基准负荷比较法、最大负荷比较法等。本文采用基准负荷比较法进行负荷分离,详细步骤见文献[18]。
1.2 负荷组合由于基础负荷与气象负荷的最大值不一定同时刻发生,若将二者直接累加,进行负荷预测时,将造成较大的误差。于是,引入同时系数β对公式(1)进行修订较为合理,具体如下:
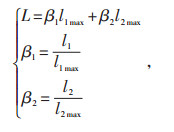
|
(2) |
式中 l1max—基础负荷最大值;
l2max—气象负荷最大值;
β1—基础负荷同时系数;
β2—气象负荷同时系数。
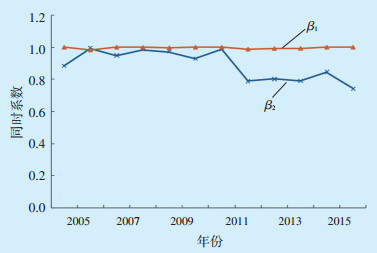
选取南方某市2005—2016年数据进行分析,β1和β2曲线如图 1。图 1表明:β1曲线非常平稳,工程应用中可近似取1;β2曲线具有较强的周期性,在一段时间内较为平稳,但随着时间推移,明显偏离1。
|
图 1 β1和β2曲线 |
由于不确定因素对负荷也有一定的影响,结合上述分析,提出一种新的负荷组合公式,具体如下:
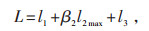
|
(3) |
其中,l3为不确定性负荷,典型的影响因素为大用户增、减产。对于l3的预测,本文仅考虑大用户这一因素。
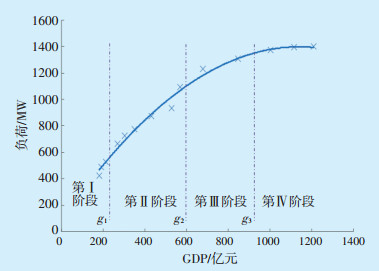
2 影响电力需求的因素分析 2.1 经济因素在经济因素的影响下,负荷发展分4个阶段:第Ⅰ阶段由于地区经济尚未成形,负荷增速较慢;受经济发展的推动,第Ⅱ阶段负荷较快生长;随着经济结构的定型,第Ⅲ阶段经济发展速度放缓,进而显现颓势;第Ⅳ阶段负荷逐步趋于稳定。选取2005—2015年南方某市的GDP、基础负荷作为变量,拟合生成负荷-经济曲线(Load-Economy Curve,LE曲线),如图 2所示。由图 2可知,从负荷生长全过程看,基础负荷与GDP呈非线性关系。
|
图 2 LE曲线 |
气象指标较多,包括温度、湿度、风速以及降雨量等。研究表明,日平均气温T与负荷的相关性最强[19]。选取T、日最大负荷作为变量,绘制负荷-温度曲线(Load-Temperature Curve, LT曲线),若同一温度对应多个负荷值,则负荷按均值处理。
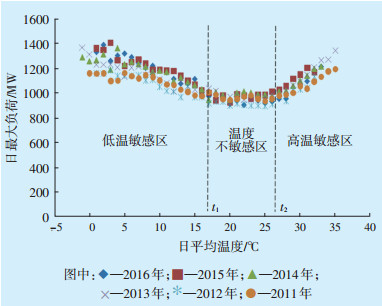
图 3为2011—2016年某市的LT曲线。温度阀值t1、t2将曲线分成3个区域,当T∈[t1、t2]时,负荷位于温度不敏感区,负荷水平处于全年低谷,且较为平稳;当T>t2或T<t1时,负荷进入高(低)温敏感区,受气象因素的影响,负荷向两侧迅速增长。气象负荷的增长主要与取暖(降温)设备的开启有关。
|
图 3 LT曲线 |
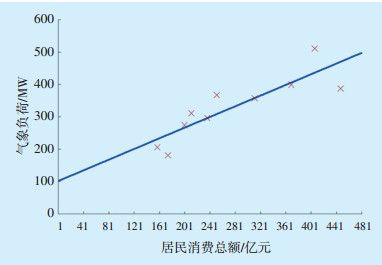
居民消费总额在一定程度上反映了地区的电器保有量水平,用该指标与气象负荷进行拟合,见图 4。由图 4可以看出,气象负荷与居民消费总额呈线性关系。
|
图 4 气象负荷与居民消费总额的关系曲线 |
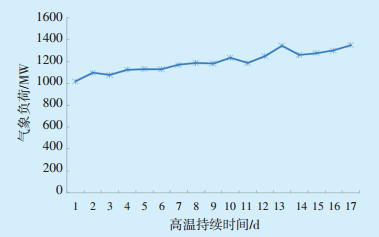
极端气温累积效应对负荷起一定的激励作用。以夏季为例,随着高温天数的增加,起初负荷缓慢上升,经过一段时间的线性“爬坡”,负荷达到最大值,见图 5所示。由图 5可以看出,气象负荷与高温持续时间也近似呈线性关系。
|
图 5 气象负荷与高温持续时间的关系曲线 |
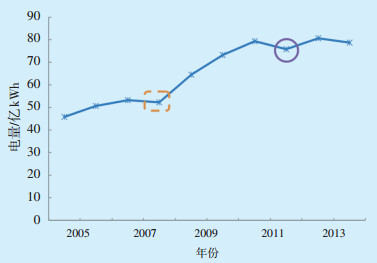
影响中长期电力需求的不确定因素有政策因素、突发性事件以及大用户增(减)产、关停等,这些因素容易造成电力曲线发生突变,从而加大负荷预测的难度。图 6为某市2005—2014年统调电量曲线,2008年、2012年曲线发生明显畸变,原因如下:受冰灾影响,2008年电网受损造成大面积持续停电,使得电力消耗明显下降;由于某大型钢企减产,2012年统调电量较上一年减少4.3亿kWh。
|
图 6 某市2005—2014年统调电量曲线 |
回归分析是基于观测数据建立研究对象(因变量)与影响因素(自变量)的解析关系,进而进行统计分析的一种方法[20]。在实际应用中,该方法用于解决预报、控制等问题,具体步骤如下:(1)确定自变量和因变量,建立回归模型;(2)显著性检验;(3)计算预测值。常用的回归模型有线性、多项式2种形式。
若因变量y和自变量x可以用如下n次多项式表示,则公式(4)为多项式回归模型。
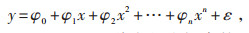
|
(4) |
式中 φ0,φ1,φ2,…,φn—待定的未知参数,称其为回归系数;
ε—随机误差。
若因变量y和自变量x1, x2, …, xn的统计依赖关系如公式(5)所示,则称为线性回归模型。
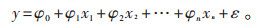
|
(5) |
回归系数常采用最小二乘法进行估计。显著性检验方法见文献[20],本文不再赘述。
3.2 多因素模型第2.1节分析指出负荷与经济因素呈非线性关系。于是选取GDP作为自变量,基础负荷为因变量,建立二次回归模型:
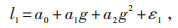
|
(6) |
式中 g—地区GDP。
气象负荷建立以居民消费总额r、极端气温持续时间t为自变量的线性回归模型:
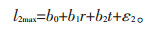
|
(7) |
在一段时间内,t对应的负荷呈线性增长;另外居民消费水平提高使得季节性电器保有量增加,从而刺激负荷增长,因此,模型(7)具有一定的合理性。
基于最大负荷利用小时数(Tmax)法,不确定性负荷的变化幅度Δl3:
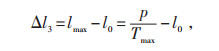
|
(8) |
式中 p—用电量;
lmax—最大负荷;
l0—正常生产时的负荷。
假设影响不确定性负荷的大用户有n家,考虑同时系数,则l3计算公式如下:
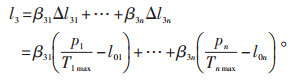
|
(9) |
令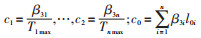
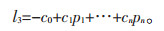
|
(10) |
记模型的随机误差为ε,结合公式(3)、(6)、(7)和(10),得到多因素的负荷预测模型:
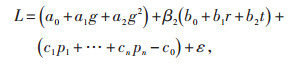
|
(11) |
其中,[a0, a1, a2]T称为a参数,[b0, b1, b2]T称为b参数,[c0, c1, …, cn]T称为c参数。
特别地,当b=c=0,a≠0时,公式(11)称为经济单因素模型(Economy Model,EM);当仅c=0时,称为经济、气象因素模型(Economy Temperature Model,ETM)。a、b、c参数分别影响了3类负荷的预测精度,因此,如何配置参数成为本文的关键问题。
3.3 参数配置l1(1),l1(2),…,l1(k)表示基础负荷的第1,2,…,k个观测值;令l1=[l1(1),l1(2),…,l1(k)]T,对公式(6)进行变换,得到线性模型如公式(12)所示:
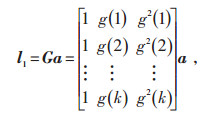
|
(12) |
其中,G为k×3矩阵。基于最小二乘法原理,多元线性回归系数的估计应满足:
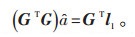
|
(13) |
为提高模型的预测准确性,观测值的组数应不少于参数个数,即k≥3,使得(GTG)存在逆矩阵。对公式(10)进行求解,得到a参数的计算公式如下:
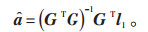
|
(14) |
同理,l2max(1),l2max(2),…,l2max(k)表示气象负荷的第1,2,…,k个观测值;令l2=[l2max(1),…,l2max(k)]T,b参数的计算公式如下:
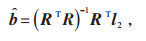
|
(15) |
式中,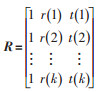
由于不确定性负荷无法直接观测,本文采用间接方法获得l3的观测值,见公式(16):
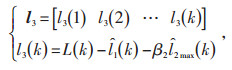
|
(16) |
其中,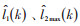
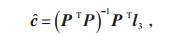
|
(17) |
式中,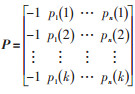
由于β2具有周期性,根据历史数据,结合工程经验选取。
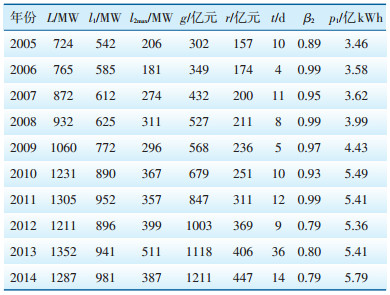
4 算例分析以某市2005—2014年相关数据作为观测值(见表 1),对该市2015年、2016年夏季最大负荷进行预测。通过与时间序列法(Time Series Model,TSM)、灰色预测(Grey Prediction Model,GM)、EM和ETM模型对比,分析MFM模型的有效性和优越性。
| 表 1 某市2005—2014年负荷等历史数据 |
地区生产总值g、居民消费总额r源于统计年鉴。t为35 ℃及以上高温持续天数。从SCADA系统中收集统调负荷数据,获得夏季最大负荷L;采用基准负荷比较法分离基础负荷l1和降温负荷l2max,通过计算得到同时系数β2。
根据相关部门发布的指标,2015年、2016年该市GDP分别为1291.4亿元和1400.1亿元,r为491亿元、540亿元,t为4 d、12 d。
对某家化工用户进行调研,年用电量p1,由于产品市场低迷,企业拟减产或适度停产,计划2015年、2016年用电量分别降至4亿kWh、2亿kWh。利用公式(14)、(15)、(17)对MFM模型参数进行配置如下:a参数为[149.6905, 1.4061, -0.0006]T;b参数为[112.5375, 0.6044, 4.1524]T;c参数为[109.8523, 22.518]T;基于经验法,2015年、2016年β2均取0.8。
采用相对误差θ和平均精度δ指标,衡量模型的有效性,定义如下:
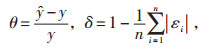
|
(18) |
式中 ŷ —模型计算值;
y—实际值。
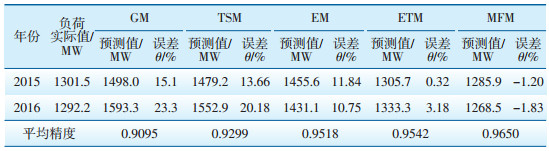
5种模型的预测值及误差比较见表 2所示。MFM模型的平均精度δMFM为0.9650,在5种模型中精度最高;从预测结果来看,2015年、2016年相对误差θMFM为-1.20%、-1.83%,较其他方法更精确。横向对比,表明本文模型的有效性。
| 表 2 5种模型预测值及误差比较 |
随着时间的推移,模型的预测误差进一步增大。GM模型2016年相对误差较上一年涨幅达到8.2%;而ETM、MFM模型仅为2.86、0.64个百分点。表明当涉及多个年份的负荷预测时,本文模型具有一定的优势。在工程实际中,TSM模型应用较为广泛。与之对比,δMFM较δTSM高出0.0351;θMFM较θTSM小,表明MFM模型具有良好的应用价值。
初期,经济因素对负荷影响较小,5种模型均能较好地跟踪实际负荷曲线。随着经济进入快车道,负荷亦快速增长,由于TSM、GM模型没有考虑经济因素的影响,负荷增速依旧保持原有水平,使得拟合值偏小;而EM、ETM、MFM模型与GDP建立了解析关系,负荷随之增长。从整体趋势来看,TSM、GM模型呈直线上升,后期预测误差较大;而本文模型均近似呈“S”形生长,更符合负荷的内在发展规律。
综上所述,MFM模型能够更准确刻画负荷生长趋势,预测精度满足工程要求。因此,多因素模型具有一定的推广价值。
5 结语针对中长期负荷预测,考虑多因素的影响,本文提出了一种数学模型以及参数配置方法。该模型能够准确刻画负荷的生长趋势,具有较好的预测精度和拟合性能。
本文深入分析了影响中长期电力需求的主要因素:气象、经济、不确定因素。采用基准负荷比较法对负荷进行分离,并指出总负荷由基础负荷、气象负荷和不确定性负荷组成;然后,将上述3类负荷分别与GDP、居民消费和极端天气持续天数以及大用户电量进行回归分析,建立直观的解析关系,进而构建多因素负荷预测模型。基于最小二乘法提出a、b、c参数的配置公式。实例表明:与传统模型对比,本文模型具有拟合性能好、预测精度高等优点,特别是MFM模型能很好地体现大用户用电信息,具有良好的工程应用价值。
| [1] |
赵希正. 中国电力负荷特性分析与预测[M]. 北京: 中国电力出版社, 2002: 151-164.
|
| [2] |
廖峰, 徐聪颖, 姚建刚, 等. 常德地区负荷特性及其影响因素分析[J]. 电网技术, 2012, 36(7): 117-125. |
| [3] |
葛斐, 荣秀婷, 石雪梅, 等. 基于经济、气象因素的安徽省年最大负荷预测方法研究[J]. 中国电力, 2015, 48(3): 84-87. DOI:10.3969/j.issn.1007-3361.2015.03.026 |
| [4] |
韦凌云, 吴捷, 刘永强. 基于系统动力学的电力系统中长期负荷预测[J]. 电力系统自动化, 2000, 24(16): 44-47. DOI:10.3321/j.issn:1000-1026.2000.16.012 |
| [5] |
李亦言, 严正, 冯冬涵. 考虑城市化因素的中长期负荷预测模型[J]. 电力自动化设备, 2016, 36(4): 54-61. |
| [6] |
吴耀武, 娄素华, 卢斯煜, 等. 基于改进的D-S证据理论的中长期负荷预测方法[J]. 电工技术学报, 2012, 27(8): 157-162. |
| [7] |
倪明, 高晓萍, 单渊达. 证据理论在中期负荷预测中的应用[J]. 中国电机工程学报, 1997, 17(3): 199-203. |
| [8] |
钱卫华, 姚建刚, 龙立波, 等. 基于短期相关性和负荷增长的中长期负荷预测[J]. 电力系统自动化, 2007, 31(11): 59-64. DOI:10.3321/j.issn:1000-1026.2007.11.013 |
| [9] |
姚李孝, 刘学琴, 伍利, 等. 基于广义回归神经网络的电力系统中长期负荷预测[J]. 电力自动化设备, 2007, 27(8): 26-29. DOI:10.3969/j.issn.1006-6047.2007.08.006 |
| [10] |
雷绍兰, 李山, 蒋东荣, 等. 重庆地区中长期负荷特性和预测方法研究[J]. 中国电力, 2016, 49(1): 96-101. |
| [11] |
王大鹏, 汪秉文. 基于变权缓冲灰色模型的中长期负荷预测[J]. 电网技术, 2013, 37(1): 167-171. |
| [12] |
张健美, 周步祥, 林楠, 等. 灰色Elman神经网络的电网中长期负荷预测[J]. 电力系统及其自动化学报, 2013, 25(4): 145-149. DOI:10.3969/j.issn.1003-8930.2013.04.027 |
| [13] |
王允平, 黄殿勋, 熊浩清, 等. 智能电网环境下采用关联分析和多变量灰色模型的用电量预测[J]. 电力系统保护与控制, 2012, 40(1): 96-100. DOI:10.3969/j.issn.1674-3415.2012.01.017 |
| [14] |
李如琦, 苏浩益, 王宗耀, 等. 应用启发式最小二乘支持向量机的中长期电力负荷预测[J]. 电网技术, 2011, 36(11): 195-199. |
| [15] |
Kandil M S, El-Debeiky S M, Hasanien N E. Long-term load forecasting for fast developing utility using a knowledge-based expert system[J]. IEEE Transaction on Power Systems, 2002, 17(2): 491-496. DOI:10.1109/TPWRS.2002.1007923 |
 2019, Vol. 37
2019, Vol. 37