2. 滨州学院, 山东 滨州 256600;
3. 乌兰察布电业局, 内蒙古 乌兰察布 012000
2. Binzhou University, Binzhou 256600, China;
3. Ulanqab Electric Power Bureau, Ulanqab 012000, China
电动汽车的迅速推广,使得对电动汽车入网技术(V2G)的研究得到重视。除了可以将电动汽车作为分布式电源来对微电网进行调峰,还可以考虑将其作为一种无功电源。国内对于电动汽车用于微电网无功补偿的研究较少,其中文献[1]研究了电动汽车在参与充电的同时进行无功补偿研究,但是未考虑电池剩余电量与电池老化问题。文献[2]则主要验证了电动汽车用于无功补偿的可行性。
对于电动汽车并入微电网用于无功补偿的问题,关键在于CSOC(电池荷电状态,电池满电量时为1,放电完毕为0)的估计,对此提出采用基于卡尔曼滤波算法的电池CSOC估计来获得电池剩余电量,设置电池剩余电量在30%时退出微电网。当电动汽车剩余电量在30%以上时,通过与安全剩余电量的差值进行比较,结合实时放电量要求,使得电动汽车参与电网无功补偿,并采用无差拍控制控制注入微电网无功功率,实现微电网无功补偿。
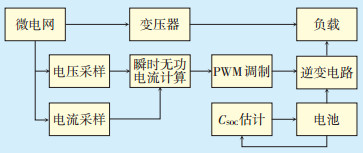
1 无功补偿方案及卡尔曼滤波CSOC估计 1.1 无功补偿方案电动汽车并网用于无功补偿主要包括微电网模块、电压电流采样模块、三相瞬时无功电流计算模块、PWM控制模块、电池模块、CSOC估计模块以及逆变器模块,电动汽车无功补偿方案见图 1。设置电池电源电压100 V,逆变器开关频率10 kHz,额定功率5 kW,微电网电压取220 V工频交流电压。
|
图 1 电动汽车无功补偿方案 |
为了得到每辆电动汽车实际可参与的放电量,首先涉及的是对电池的CSOC精确估计,电池CSOC的计算公式为:
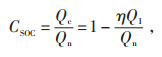
|
(1) |
式中Qn—电池总容量;
Qc—电池剩余容量;
QI—电池实际可用电量;
η—电池效率[2]。
其次是电池的模型需要准确描述,常用的动力电池数学模型为:
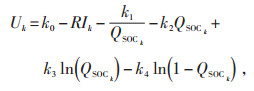
|
(2) |
式中Uk—电池在k时刻的端电压;
R—电池电阻值;
Ik—k时刻电池电流;
QSOCk —电池在k时刻测得的剩余电量,其中系数k0、k1、k2、k3、k4根据试验数据通过系统参数辨识得到[3],其取值如表 1所示。
| 表 1 电池模型系数 |
建立电池模型后,采用卡尔曼滤波算法进行CSOC估计,其采用电池前一时刻的CSOC估计值和当前时刻的观测值来更新当前的CSOC估计状态方程,得到当前时刻CSOC估计值,其状态与观测方程为:
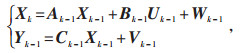
|
(3) |
式中Xk-1—k-1时刻状态向量;
Xk—状态向量;
Yk-1—前一时刻观测向量;
Uk-1—控制向量;
Ak-1—系统矩阵;
Bk-1—控制输入矩阵;
Ck-1—量测矩阵;
Wk-1—过程噪声;
Vk-1—观测噪声。
电池的CSOCk具有如公式(4)所示关系:
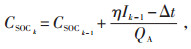
|
(4) |
式中CSOCk—电池k时刻荷电状态;
CSOCk-1—电池k-1时刻荷电状态;
Ik-1—电池k-1时刻放电电流值,在这里取负;
t—采样时间;
QA—电池额定容量。
根据公式(4)可得到卡尔曼滤波估计CSOC的状态和观测方程:
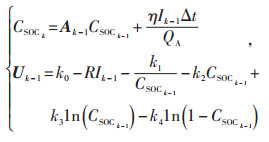
|
(5) |
其中,Uk-1为k-1时刻电池电压。
对CSOCk - 1求偏导,见公式(6):
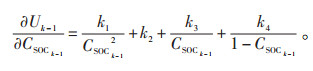
|
(6) |
时间和量测更新方程为:
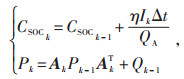
|
(7) |
式中Pk—k时刻的估计误差;
Pk-1—k-1时刻的误差值;
Ak—k时刻系统矩阵;
AkT—对k时刻系统转置矩阵;
Qk-1—k-1时刻电池容量。
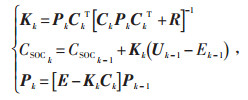
|
(8) |
式中Kk—k时刻卡尔曼增益;
CSOCk—k-1时刻对k时刻最优估计值;
CSOCk-1—k-1时刻最优估计值;
Pk—最优估计值的误差矩阵;
E—单位矩阵;
CkT —对k时刻量测转置矩阵;
Ck—k时刻量测矩阵;
Uk-1—k-1时刻控制向量;
R—电阻矩阵。
通过上述方程可以得到电池的实时CSOC值,使得电动汽车在电池余量接近30%时退出电网。
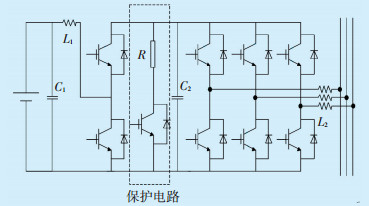
2 V2G电路结构及无差拍控制 2.1 V2G能量变换拓扑结构在本文中,电动汽车的输出电压首先通过直流斩波电路升压,接着通过三项逆变电路逆变为工频交流输入电网,因此采用图 2的三相电力变换拓扑结构,包括电网侧三相逆变电路、保护电路和电池侧Boost斩波电路。中间的保护电路主要是为了防止斩波电路输出电压急剧变化,用于保护电路[1]。
|
图中:L1—直流侧滤波电感;C1—直流侧滤波电容;L2—交流侧滤波电感;C2—交流侧滤波电容 图 2 V2G能量变换拓扑结构 |
三相瞬时无功功率理论是一种实时检测瞬时有功功率与无功功率电流的方法[4],先将三相电压进行α-β变换,如公式(9):
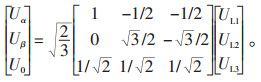
|
(9) |
则三相电流如公式(10):
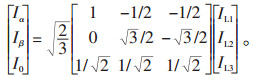
|
(10) |
变换得到额定电压U和电流I之后,如果将额定电压U标幺化,取值为1,此时Uα和Uβ有:
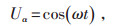
|
(11) |
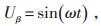
|
(12) |
由此可以得到公式(13):
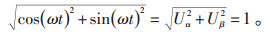
|
(13) |
计算得到解耦后的有功电流Ip和无功电流Iq:
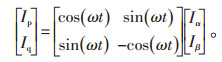
|
(14) |
以上就是通过三相瞬时无功功率理论来测量实时无功电流的过程,该理论通过Ip-Iq分解法实现有功无功电流的解耦,得到的无功电流主要用于无差拍控制的输入。
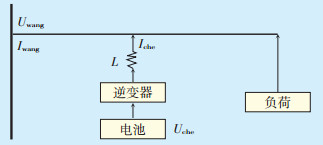
2.3 无差拍控制通过三相瞬时无功电流计算得到解耦后的无功电流,该电流用作前一时刻电动汽车并入微电网电流Iche(电池侧),带入公式(17)。图 3中将单个电动汽车并网系统简单划分为电网、电池和逆变器。
|
图中:Iche—电池侧电流;Uche—电池侧电压;Uwang—网测电压;Iwang—网测电流;L—电感 图 3 电动汽车并网示意图 |
需要对微电网实时无功电流做出抵消补偿,使得电动汽车Iche与微电网无功电流Iq相等,相位相反,以完成无功电流补偿。在这里,无功和有功电流来自三相瞬时检测模块,Iche作为控制电流,采用无差拍控制具有公式(15)的关系:
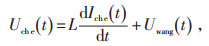
|
(15) |
其中,L为并联微电网侧需要经过的1个电感,用于滤除高次谐波,Uwang(t)则是t时刻微电网侧电压。将上述方程进行差分,则有公式(16):
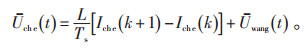
|
(16) |
其中,Uche(t)和Uwang(t)分别是1个采样周期的电动汽车电池侧与电网侧电压均值,Ts为采样时间。
之后将Iche(k+1)用参考电流Ican(k+1)代替,可计算得到IGBT(绝缘栅双板型晶体管)开关管在每一段采样期间的占空比D(K),具有公式(17)的关系:
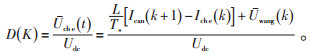
|
(17) |
在式(17)中,将Uwang(k)展开的表达式为:
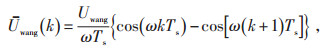
|
(18) |
其中,Uwang为电网输入侧电压的最大值,Udc为直流电压。
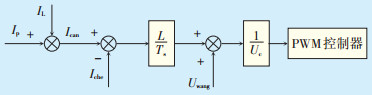
通过公式(17)可以看到,对于参考电流Ican(k+ 1)的控制可通过改变D(K)来完成。这个过程可以用图 4来表示。
|
图中:Uc—电池电压 图 4 无差拍控制过程图 |
如果图 4中的Iche=Ican,就可保证微网测电流Iwang=Ip,使微电网电流中只含有功分量,从而使得微电网的无功功率得到全补偿。
3 仿真及试验搭建电动汽车并入微电网用于无功补偿仿真模型。仿真参数为:Udc=100 V,Uwang取其幅值220 V,频率为50 Hz,电抗与电阻比值X/R取7,三相负载R=6 Ω,L=10 mH,逆变器中L1=3 mH,C1=50 μF,C2= 2200 μF,R=20 Ω,L2=1.5 mH,仿真时间为10 s,逆变器开关频率为10 kHz[5]。
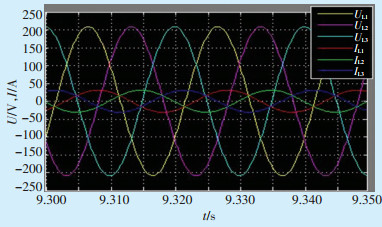
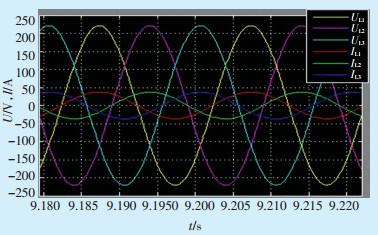
图 5为采用前馈解耦控制得到的电压电流相位关系图,图 6为采用无差拍控制电压电流相位图,对比2图,发现采用无差拍控制算法后电压电流同步效果更好,功率因数约为1。
|
图 5 前馈解耦控制电压电流相位图 |
|
图 6 无差拍控制电压电流相位图 |
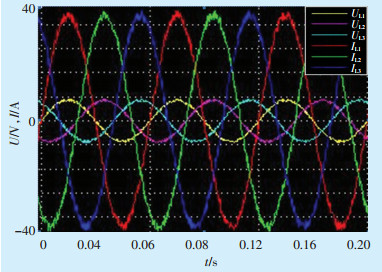
为了进一步验证方案的可行性,搭建基于TMS320F28335的试验台,设置电池电压为30 V,负载采用容性负载,设置R=6 Ω,C=800 μF,电网侧电压设置为40 V。试验结果如图 7所示。
|
图 7 试验结果图 |
该试验结果与仿真试验结果相同,经过无功补偿后,电压电流基本达到同相位。
4 结语在不影响日常出行情况下,通过卡尔曼滤波算法精确估计CSOC,采用瞬时无功电流Ip-Iq分解得到无功电流,通过无差拍控制实现了电动汽车并入微电网补偿无功功率问题[6-8]。通过仿真与搭建试验平台对方案进行验证,结果表明采用无差拍控制比前馈解耦控制能够更好地解决微电网无功功率不足问题,增加了电动汽车并入微电网时的适用范围。但是本文只研究了1台电动汽车参与微电网并网时的无功补偿,对于大规模电动汽车集群并入高压电网进行无功补偿需要进一步研究。
| [1] |
满洲, 郭春林, 裴鑫, 等. 基于V2G的电动汽车无功功率补偿技术[J]. 现代电力, 2018, 35(4): 15-20. DOI:10.3969/j.issn.1007-2322.2018.04.003 |
| [2] |
Kisacikoglu M C, Ozpineci B, Tolbert L M. Uxamination of a PHUV bidirectional charger system for V2G reactive power compensation[C]//Applied Power Ulectronics Conference and Uxposition. IUUU, 2010: 458-465. https://ieeexplore.ieee.org/document/5433629
|
| [3] |
杜晨.智能电网下电动汽车电池管理系统的研究与设计[D].合肥: 合肥工业大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10359-1013377448.htm
|
| [4] |
李建林, 张仲超. 关于谐波及无功电流检测方法的综述[J]. 电力系统及其自动化, 2003, 159(4): 89-93. DOI:10.3969/j.issn.1003-8930.2003.04.024 |
| [5] |
周渊深, 朱希荣, 宋永英, 等. 电力电子技术与MATLAB仿真[M]. 北京: 中国电力出版社, 2014: 199-209.
|
| [6] |
朱鹰屏, 张绪红, 韩新莹. 用于配电网网损优化的电动汽车智能充电调度[J]. 广东电力, 2016, 29(9): 94-97, 103. DOI:10.3969/j.issn.1007-290X.2016.09.019 |
| [7] |
严勤, 曾洁. 电动汽车的充电模式及充电设施建设运营模式研究[J]. 电力大数据, 2018, 20(1): 39-42. |
| [8] |
严玉廷, 陆海. 电动汽车V2G在含光伏的配电网中的经济性研究[J]. 云南电力技术, 2018, 46(4): 110-115. DOI:10.3969/j.issn.1006-7345.2018.04.032 |
 2019, Vol. 37
2019, Vol. 37 

