2. 国网湖北省电力有限公司宜昌供电公司, 湖北 宜昌 443000
2. Yichang Power Supply Company of State Grid Hubei Electric Power Company, Yichang 443000, China
随着我国高压直流输电(HVDC)的快速发展和交直流联网的出现,需要对不同交直流系统的相互影响进行更深入的研究,电磁暂态仿真是必不可少的手段之一[1-3]。目前针对直流输电的电磁暂态仿真研究大多采用PSCAD或MATLAB/SIMULINK软件,并基于国际大电网控制模型CIRGE第Ⅰ类Benchmark模型对HVDC控制系统进行研究[4]。但PSCAD、MATLAB/SIMULINK作为离线仿真软件,受其仿真周期限制,难以反映系统运行与控制动态全过程;尤其是CIRGE-Benchmark控制模型为最简静态模型,无法得出与实际工程相符的仿真结果[5]。
本文参考实际系统现行控制策略,使用实时数字仿真器RTDS建立HVDC输电系统动态模型。首先,依据HVDC实际控制中整流侧采用反馈式变增益的定电流控制、逆变器采用最大点火角和定电流控制策略,对换流器触发角控制进行建模;其次,在角度与档位协调机制下建立变压器分接头自动调节模型;最后,基于RTDS构建典型的HVDC输电系统一次主回路模型,并在额定工况校正基础上对触发角控制、变压器分接头调节等功能进行多工况动态响应测试。
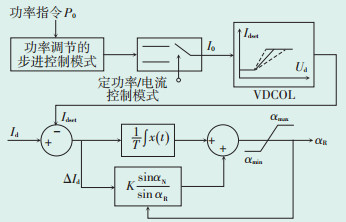
1 换流器触发角控制 1.1 整流侧点火角的确定直流控制中必不可少的直流电压-电流(Ud-Id)特性曲线,确定了直流系统在稳态、小扰动和动态过程中整流、逆变两端控制器的基本配合原则[6]。整流侧最常用的控制方法是以Id为控制对象,将之与整流侧触发角αR形成反馈控制,即电流控制放大器。与CIRGE标准测试模型中使用常规PI调节器进行触发角控制相比,实际中采用反馈式变增益的PI调节器产生点火角,形成直流电流的闭环控制,据此建立的αR调节器模型如图 1所示。
|
图中:P0—功率指令值;Idset—电流指令值;Idmeas—Id的测量值;Idest—Id的整定值;αmax—αR的上限;αmin—αR的下限;αN—整流侧额定触发角;Io—Id的指令输出值 图 1 整流侧αR调节器模型 |
图 1中,极功率控制中的P0经功率调节的步进环节输出,并选择定功率或电流运行模式,在低压限流环节(VDCOL)作用下给出Idset。当直流电压降低时,VDCOL通过降低电流指令使直流系统在交流系统受到扰动时保持功率稳定。电流控制放大器采用Idmeas与Idset的偏差ΔId经PI环节确定αR。当Idmeas < Idset时,αR在PI作用下减小,同时使得PI中比例系数增大,从而使αR快速减小和Id迅速增大;当Idmeas>Idset时PI变增益的作用相反,保证αR快速增大以及Id迅速变小。αN在工程中设计为15°;αmax可取闭锁阀组时的90°;αmin一般为50°。
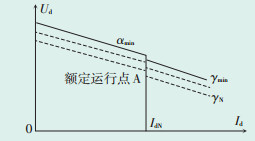
1.2 逆变侧点火角的确定逆变侧的控制必须与整流侧配合,以满足Ud-Id工作点是稳定的运行点[7]。正常工况时逆变侧采用最大点火角控制,以使熄弧角γ不小于其下限值γmin,从而避免换相失败;整流侧调节器能够在αR的限制范围内使Id达到额定电流IdN,运行工况如图 2所示。
|
图中:γmin——熄弧角下限值;IdN—额定电流;γN——熄弧角额定值 图 2 正常工况时逆变侧控制 |
图 2中,γmin为130°,γN为170°。在CIRGE标准测试模型中,为了实现逆变侧的定熄弧角控制,用测量所得γ与γN的偏差经PI环节确定逆变侧触发角αI。本文通过最大点火角控制以确定αI,该方法计及实际空载直流电压Udio的影响,并依据点火角非线性控制的特征进行设计,即:
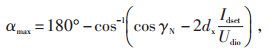
|
(1) |
其中,dx为换流变压器的换相电抗。
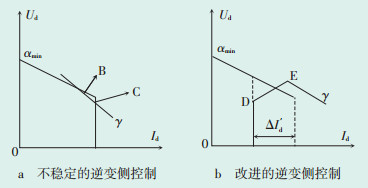
当交流系统电压出现波动使整流侧母线电压过低或逆变侧母线电压过高时,整流侧调节器即使运行至αmin也无法使Id达到额定值IdN,这时整流侧已转为定αmin控制,而逆变侧应转为定电流控制(一般电流裕度ΔId ′ = 0.1IdN)[8]。逆变侧若仍采用正常运行时的定αmin控制,如图 3a所示,直流系统呈现不稳定的2条平行特性曲线,造成Id左右波动。因此在逆变器控制特性中将原负斜率的定γ特性修改为正极性斜率特性(D-E),对公式(1)作出修正:
|
图 3 两种逆变侧控制方式 |
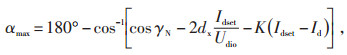
|
(2) |
图 3b中的修正也起到了稳固控制系统的作用,没有这个正极性斜率,整流器将视逆变器为1个低频负极性阻抗。当交流电压出现异常时,电流控制可以转移到逆变器,对于电流下降的系统提供了1个自动的补偿。在实际中逆变侧的定电流控制与定熄弧角控制是不允许同时工作的,故在RTDS模型中采用如图 4所示方法。
|
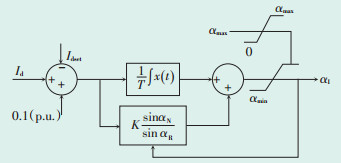
图 4 逆流侧αI调节器模型 |
图 4中,αmax为式(1)在γmin条件下的触发角,αmin取110°。逆变侧电流调节器采用与整流侧相同的变PI增益控制方式,所不同的在于电流偏差输入。逆变侧通过引入0.1p.u.的电流增量以实现图 3b中的电流裕度ΔId ′,同时也可保证在正常工作下电流调节器的输出必然大于αmax,即正常运行时最大点火角控制αI=αmax。当交流系统电压波动使得Id < 0.9Idset时,αmax增大,而电流调节器的输出减小,这时αI不再受αmax的限制,逆变侧从而转到定电流控制[9]。
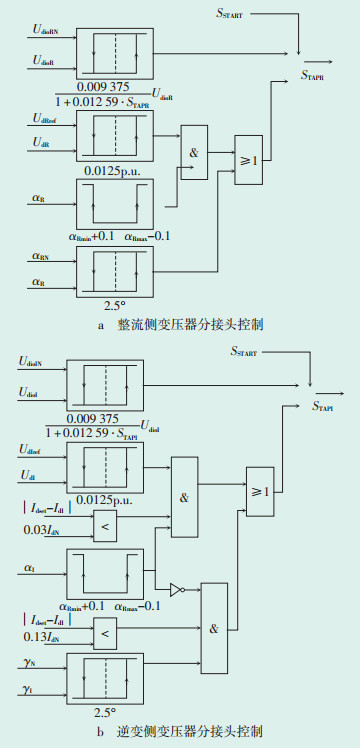
2 变压器分接头控制变压器分接头控制模型是直流控制系统中用于自动调整换流变压器分接头位置的1个环节,其功能是配合换流器触发角控制中的电流调节器保持整流器的触发角(或逆变侧的关断角)以及直流极母线电压运行于合适的范围内,该模型具有3个调节功能,即调节理想空载直流电压Udio、Ud和点火角α。其结构如图 5所示。
|
图中:UdioRN—整流侧理想空载直流电压;UdioR—空载直流电压实测值;UdRref—额定直流电压;UdR—直流电压实测值;STAPR—换流变分接头调压信号;UdioIN—逆变侧理想空载直流电压;UdioI—空载直流电压实测值;UdIref—额定直流电压;UdI—直流电压实测值;αRN—整流侧触发角额定值;αRmax—整流侧最大触发角;αRmin—整流侧最小触发角;αI—逆变侧触发角;γI—逆变侧息弧角;STAPI—换流变分接头调压信号;SSTART—阀组点火控制信号 图 5 变压器分接头控制结构 |
图 5中,在阀组启动(点火)前,变压器分接头控制模型根据交流母线电压自动将Udio调整至额定值(1±0.009 375)p.u.,同时为了确保变压器分接头在启动过程中不动作,点火后10 s内需闭锁调压和调角度功能。
与电流调节器平滑连续调节方式不同,变压器分接头控制为分级间断式调节(上升指令时间间隔≥2 s、下降指令时间间隔≥1 s);整流侧电压调节值为(1.03±0.0125)p.u.、角度调节值为(15°±2.5°);逆变侧电压调节值为(1.00±0.0125)p.u.、角度调节值为(17°±2.5°)。
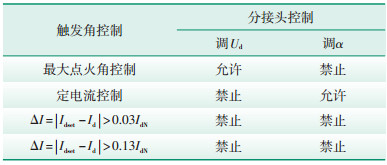
整流器和逆变器的换流变压器分接头控制与换流器触发角控制的配合分别如表 1和表 2所示。
| 表 1 整流侧换流变分接头控制与阀组触发角控制的配合 |
| 表 2 逆变侧换流变分接头控制与阀组触发角控制的配合 |
从表 1和2可知,逆变站的变压器分接头控制结构与整流站相同,但多了一些闭锁条件限制,一是正常控制(最大点火角)情况下,变压器分接头控制的角度调节功能被触发角信号(αI>αImax-0.1)闭锁;二是受电流偏差ΔI = |Idset -IdI |闭锁,当标幺值ΔI大于3%时闭锁调压作用、当ΔI大于13%时闭锁调角度作用,这说明当整流站处于电流调节暂态过程期间,逆变站变压器是不允许调档位的。
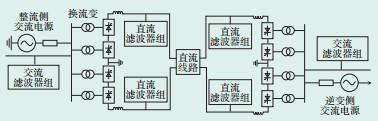
3 模型仿真分析采用典型双桥12脉动HVDC输电系统,其参数为:额定功率3000 MW,额定电压500 kV,额定电流3 kA,平波电抗器为0.27 H,直流线路长度960 km(采用贝杰龙模型)。整流侧交流系统额定电压525 kV、短路容量18 523 MVA、额定频率50 Hz;逆变侧交流系统额定电压500 kV、短路容量31 486 MVA、额定频率50 Hz。两端换流站分别装设有140 Mvar和190 Mvar的无功补偿装置,包括3次C型、11和25次双调谐交流滤波器。一次回路中的阀组、换流变压器、直流滤波器等元件模型直接按实际设备的设计参数建立,采用RTDS内部库元件构建如图 6所示一次主回路模型。
|
图 6 HVDC一次主回路RTDS模型 |
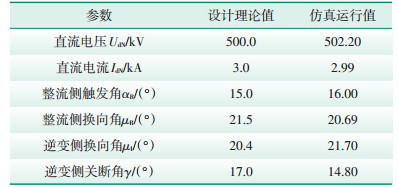
为了检验一次回路试验模型本身能否按设计要求模拟运行,采用本文所述触发角控制模型作为RTDS内部软件控制器。内部触发角控制模型可用于调整两侧戴维南电源电压,使一次回路模型运行于额定工况。经反复调整后一次回路模型在额定工况下的检验结果如表 3所示。
| 表 3 模型校验结果 |
从表 3可以看出,在计及仿真步长所引起的误差条件下,该一次模型在额定工况下仿真运行值与理论值相符。而逆变侧关断角的仿真运行值与设计理论值有些差距,这是由于本文所建立的逆变侧最大触发角控制在实现定γ控制的同时,尽可能保证γ较小以降低换流器所消耗的无功功率。测试所得两侧等效戴维南电源初始电压分别设置为560.77 kV、496.27 kV。
3.2 控制模型动态响应为了测试高压直流输电系统中换流器触发角与变压器分接头控制的动态响应特性,采用已建立的RTDS模型,在定功率运行条件下,当逆变侧换相母线额定电压保持不变时,整流侧换相母线电压下降(换相母线电压从1.0p.u.降至0.9p.u.),直流系统的动态响应特性如图 7所示。
|
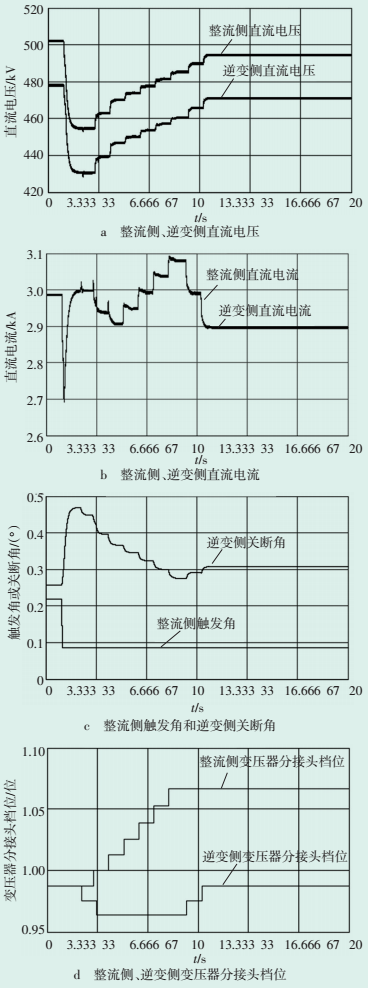
图 7 整流侧换相电压下降时直流系统动态响应 |
从图 7可知,当整流侧换相母线电压下降时,整流侧触发角进入αmim状态,而逆变侧转为定电流控制,即直流电流变为2.7 kA,但之后逆变侧转为最大点火角控制。随着整流侧变压器分接头档位上升和逆变侧变压器分接头档位下降,直流电压逐渐恢复,逆变侧关断角从较大值逐渐回到正常运行区间。其整体动态过程的Ud-Id特性曲线如图 8所示。
|
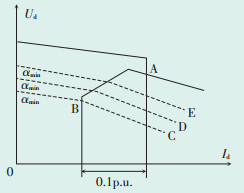
图中:A—初始运行点;B—整流侧处于αmim控制、逆变侧处于定电流控制时的运行点;C、D、E—变压器分接头动作下逆变侧关断角逐渐变小时的运行点 图 8 整流侧换相电压下降时直流系统Ud-Id特性曲线 |
可见,在电流控制放大器、最大点火角控制以及变压器分接头作用下,该模型具有较好的动态响应特性,基本满足直流输电运行要求。
4 结论本文基于RTDS针对典型直流输电系统一次主回路结构建立了详细的仿真控制模型,并在额定工况校核的基础上对模型进行了多工况动态响应测试。结果表明:换流器触发角控制模块可实时模拟整流/逆变侧的电压、电流快速变化过程;变压器分接头控制模块亦具有理想空载直流电压Udio、直流电压Ud、触发角α的自动调节仿真功能,且能反映出与触发角控制的动态协调过程。
| [1] |
雷霄, 许自强, 王华伟, 等. ±800 kV特高压直流输电工程实际控制保护系统仿真建模方法与应用[J]. 电网技术, 2013, 37(5): 1359-1364. |
| [2] |
罗磊, 盛琰, 王清坚, 等. 特高压直流输电系统顺序控制的研究[J]. 电力系统保护与控制, 2011, 39(23): 30-33. |
| [3] |
李兴源, 赵睿, 刘天琪, 等. 传统高压直流输电系统稳定性分析和控制综述[J]. 电工技术学报, 2013, 28(10): 288-300. DOI:10.3969/j.issn.1000-6753.2013.10.035 |
| [4] |
Manitoba HVDC Research Center Inc. PSCAD user's guide[M]. Winnipeg: Manitoba HVDC Research Center Inc, 2003: 234-237.
|
| [5] |
常浩, 张民, 马为民. 实时数字仿真器的应用[J]. 中国电力, 2006, 39(7): 56-60. |
| [6] |
陶瑜, 韩伟. 高压直流输电控制保护技术及其应用[J]. 电力设备, 2004, 5(11): 4-8. |
| [7] |
张凤鸽, 张凤武. 高压直流输电极控系统的RTDS模型[J]. 华中电力, 2006, 19(1): 6-8. DOI:10.3969/j.issn.1006-6519.2006.01.002 |
| [8] |
张建设, 张尧, 张志朝, 等. 直流系统控制方式对大扰动后交直流混合系统电压和恢复的影响[J]. 电网技术, 2005, 29(5): 20-24. DOI:10.3321/j.issn:1000-3673.2005.05.005 |
| [9] |
胡艳梅, 吴俊勇, 李芳, 等. ±800 kV哈郑特高压直流控制方式对河南电网电压稳定性影响研究[J]. 电力系统保护与控制, 2013, 41(21): 147-153. DOI:10.7667/j.issn.1674-3415.2013.21.024 |
 2019, Vol. 37
2019, Vol. 37