近年来,我国多地出现因空气污染造成的雾霾天气,给广大市民带来不便,而燃油汽车排放是主要污染源之一。缓解上述问题的关键方法之一是推广使用具有环保特点的电动汽车,而电动汽车充电站作为电动汽车补充电能的基础设施,是电动汽车规模化推广的重要保障。因此对电动汽车充电站的合理规划是很有必要的。
电动汽车充电站规划是组合优化问题,具有动态性、多目标性、非线性等特点,目前充电站规划常用方法大致分为2类:数学规划优化方法和启发式规划优化方法。数学规划方法是解决决策系统的多变量优化问题,该方法研究时间最早并且使用最成熟,在电动汽车充电站的早期和中期规划中几乎所有研究环节都用到了数学规划优化方法[1-5]。Toregas等提出了集覆盖问题,在满足所有需求的约束下使服务设施的建设成本最小化[2]。2015年张争辉提出基于Voronoi图与改进PSO算法的充电站规划方法[6]。启发式规划方法是依靠事物表现特征来启发算法的行为特征,该方法首先需要对待解决问题进行直观分析,确定系统中可行路径上的线路参数对该系统某个性能的灵敏程度,然后以得到的分析结果为依据,根据一定的原则(规则)逐步迭代。主要包括模拟退火算法、遗传算法、粒子群算法、蚁群算法等[7-8]。
本文使用Pareto蚁群算法对充电站分布进行初步规划,之后利用充电站的历史负荷信息预测下一阶段负荷[9-13],为充电站后期调整与扩充提供依据。
1 充电站站点规划数学模型 1.1 规划步骤本文从充电站的经济效应、用户便利性两方面分析汽车充电站的规划问题。其中充电站的经济效应主要影响因素有初始建成成本、运行成本等。用户便利性主要指用户的充电时间成本以及车辆的行驶成本。最终通过求解车辆行驶的较优路径以及企业的经济效益来确定充电站的规划方案。具体步骤如下。
(1) 构建待规划的公路网站点结构信息。
(2) 从路径网中选择电动汽车可以到达终点的站点规划,站点规划要求使站点建立的经济代价最小和车辆的行驶成本最小。建立模型时对该问题做出假设,考虑公路的交叉路口设站点,如果该交叉路口到下一交叉路口建设站点成功,则路径中按能耗要求设立站点。
(3)依据经过该站点的车流量和车辆类型,车辆的行驶成本和充电成本,车辆在某站点处的充电成本由该站点的电能成本来确定。
(4)依据交通拓扑图中站点之间的距离、站点的车流量、通过车辆的车辆类型、地理位置信息、电能来源、与上一站之间的关系来确定该站点的建设成本和运营成本。
(5)在实际公路网中存在这样的问题,不同终点或不同起点会经过相同的站点,当建设第2条联通站点路线时,通往起点和终点的某些站点已经存在,因此在建模中需要区分候选站点和已建站点。
1.2 数学模型根据实际需求建立数学模型和规划算法,充电站的初始模型是在路网的起点和终点之间的多条可达路径中建立1条电动汽车行驶路径,线路结构决定了充电站规划模型的解空间,拓扑结构中的节点表示预设的充电站点。最优化充电站规划模型的数学描述如下。
(1)经济成本目标函数:
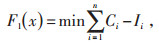
|
(1) |
式中 Ci—建设成本及运行成本;
n—站点数量;
Ii—经济效益。
Ci定义为:
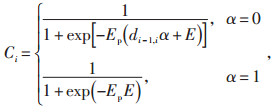
|
(2) |
式中 α—站点之间的距离与成本的相关系数;
di-1, i—站点与上一站点之间的距离;
Ep—站点电能来源;
E—站点本地投放成本,与站点位置相关。
(2)经济效益Ii的计算公式:
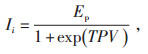
|
(3) |
式中 V—站点的车流量;
T—站点通过车辆中小型车辆的比例;
P—充电站规模。
(3)车辆的行驶成本计算公式:
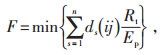
|
(4) |
式中 F—车辆的行驶成本;
ds(ij)—站点i到下一站点i+1的距离;
Rt—不同类型的电动汽车对应的每千米耗电量;
s—第i步可以选择的前进路径数量。
2 基于Pareto蚁群算法的充电站规划 2.1 规划原理Pareto蚁群算法是1种多目标单种群蚁群算法[14],路径上对应的多个目标由多个信息素表示。开始阶段随机确定多个目标的权重pk,0≤pk≤1,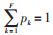
蚂蚁完成1次周游后,在行进的路上释放信息素,同时路线上原信息素适当挥发。蚂蚁路径根据信息素强度大小选择,同时考虑站点的经济效益和车辆到该站的行驶成本,每只蚂蚁只能走合法路线,为此设置禁忌表控制。
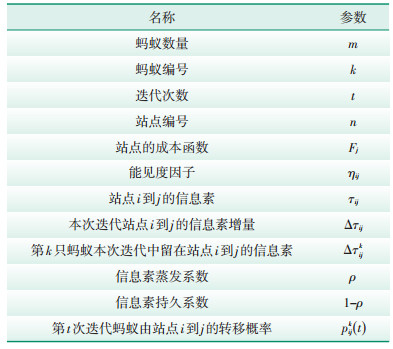
2.1.1 参数初始化最大迭代次数设为Nmax,每段路线上的权重为在该路线终点建立充电站的经济成本以及车辆从该路线起到到终点的行驶成本。二维禁忌表初始化为空。各参数定义如表 1所示。
| 表 1 参数定义 |
位于站点i的蚂蚁k在第t次迭代时,选择下1个站点j的概率为pijk(t)。
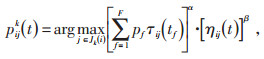
|
(5) |
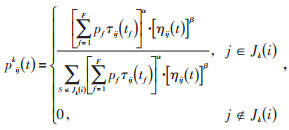
|
(6) |
式中 F—目标函数个数;
pf—目标函数权重;
α—累积信息的系数;
β—启发信息的系数;
Jk(i)—蚂蚁可到达的站点。
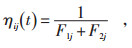
|
(7) |
式中 F1j—站点j的经济效应;
F2j—车辆从站点i到j的行驶代价。
2.1.3 更新策略当前最优方案上的路径,按公式(3)和(4)更新信息素:
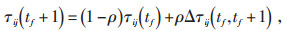
|
(8) |
其中,Δτij(tf, tf+1)定义如下:
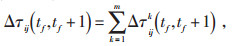
|
(9) |

|
(10) |
式中 Qf—蚂蚁循环1周路径上释放的信息总量;
Ff—蚂蚁循环1周路径上累积的信息总量。
当蚂蚁均完成1次搜索时不在路径上的信息按公式(11)更新:
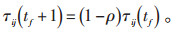
|
(11) |
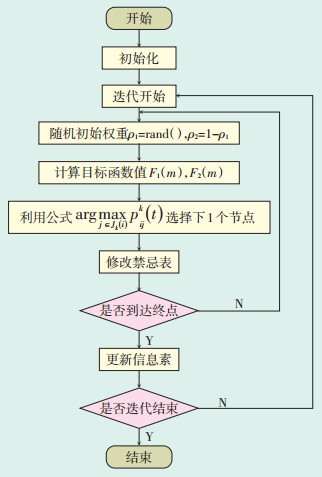
Pareto算法和单目标蚁群算法相比增加了权重确定过程及信息素更新过程,具体流程见图 1所示。
|
图 1 Pareto蚁群算法流程图 |
在规划初期中使用电动汽车充电站设施规划的模型和算法,对不同起点和终点之间进行合理的充电设施规划。由于高速公路的车流量实时变动,因此电动汽车充电的负荷预测对调整充电站规划具有重要意义。首先,充电站负荷预测是站点优化的基本依据,通过对站点负荷的预测可以确定是否进行站点扩建,并确定新建站点的相关规模。其次,站点负荷预测可以为电网的配电提供可靠依据。
3.1 BP神经网络模型BP神经网络是一种误差逆向传播神经网络模型,其具有较强的非线性映射能力。BP神经网络在训练时,能够自动对输入数据和目标之间的联系建立规则[15-17]。在正向传播过程中,输入层得到输入特征后,与第一个隐藏层进行点对点加权求和计算,后续隐藏层将前一隐藏层的输出作为输入重复上述计算过程,输出层计算得到输出结果。网络在反向传播阶段,利用正向传播最后输出的结果逐层求出目标函数对各神经元权值的偏导数,完成网络的学习。
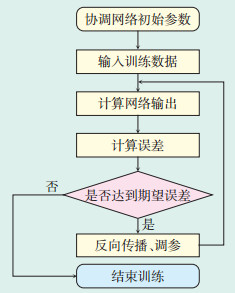
3.2 基于BP神经网络的充电站负荷预测本文对站点预测的主要目的是对电动汽车充电站点的扩展及为电网配电提供参考,预测时分别按月预测,利用前几年每月站点负荷数据预测下1年度该月负荷。基于BP神经网络电动汽车充电站负荷预测的实现步骤如图 2所示。
|
图 2 BP神经网络电动汽车充电站负荷预测流程图 |
利用预测得到的站点充电负荷扩展站点并为配电提供依据。当站点负荷超过规定阈值或预测未来会达到该阈值,则利用Pareto蚁群算法扩展与该站点连通的其他站点。扩展时需要考虑该起点到终点所有站点的负荷均值,如路径上的负荷均值相对阈值较低,则不扩展整条路径,仅扩展该站点的规模,否则扩展整条路径。
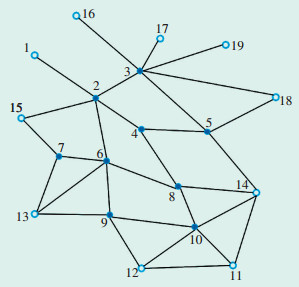
4 实例分析 4.1 充电站规划本文仿真设计1个高速路网案例进行仿真计算,其拓扑图如图 3所示。
|
图 3 高速公路待选站点拓扑图 |
此高速路网共有待扩充交叉路口站点9个,城市共10个,城市可以视作终点或起点,不对起点、终点做充电站规划,市区默认有充电站站点。试验初始站点规划选择从起点1到终点11之间的站点建立充电站。
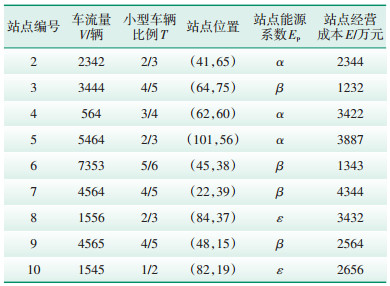
本文考虑交叉路口是否设立站点,并同时确定到下1个交叉口之间的所有站点,不考虑该路口到下1路口电能是否能满足到达需求。使用到的站点参数设置为:d表示路径上前1个充电站到下1个充电站之间的距离,在寻优过程中动态变化;Rt表示不同类型的电动汽车对应的耗电量,是常量;P为充电站规模,试验中设定该值为常数。待布充电站站点初始数据如表 2所示(本站点数据为仿真数据),α= 0.8,β=1.5,ε=1.2。
| 表 2 站点参数配置 |
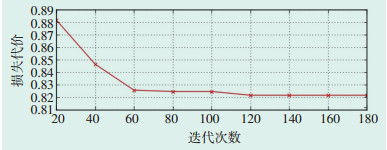
通过Pareto蚁群算法对19个候选站点进行规划,站点1和站点11分别作为规划路线的起点和终点,迭代收敛效果如图 4所示。寻优结果如图 5,从1号起点到11号站点的寻优路径为1→2→6→9→10→11。
|
图 4 Pareto蚁群算法迭代收敛效果 |
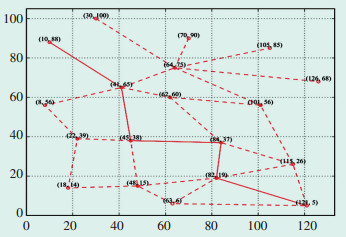
|
图 5 站点选择路径 |
随着充电站的建设完成,为了更便捷地为电动汽车充电,需要对已建成的充电站进行优化和扩充,本文使用站点负荷作为站点扩充优化的依据。负荷预测不仅可以辅助充电站网络的优化和扩充,还可以为电力配电提供参考。
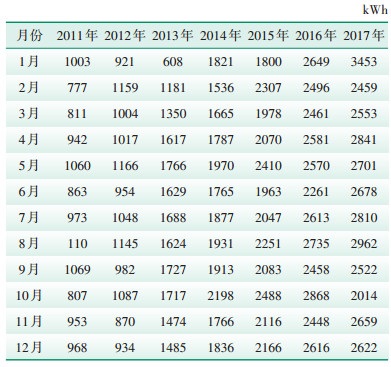
充电站的负荷与相应路段的车流量有密切关系,本文参考某高速路段车流量来仿真高速公路充电站站点7 a内不同年份不同月份的负荷数据,某一站点数据如表 3所示。网络训练需要较多的训练数据,实际训练时仿真多个站点多条数据,训练集包括19个站点288条数据。
| 表 3 某站点7a内不同月份负荷数据 |
对数据进行预处理,使数据规范到[0, 1]。网络参数配置如下:隐藏层单元个数分别为10、6。输入层单元个数设置为5,输出层单元个数为1,网络训练过程中权重和偏置随机初始化。训练结束条件设置为误差小于0.001或迭代次数达到10 000停止训练。
4.3 预测结果及分析输入前5a内某月的负荷得到下1a该月的预测负荷,经过验证发现,相比于混合高斯、函数拟合,BP网络的预测准确率更高。但是此次试验的准确率还不够理想,主要原因是站点仿真负荷数据量较少,仿真得到的数据量在进行网络训练中出现了欠拟合现象,造成网络学习到的特征信息不足。因此,若有充足的数据训练BP网络时,可以获得较为准确的站点负荷预测,充电站规划将得到进一步优化。
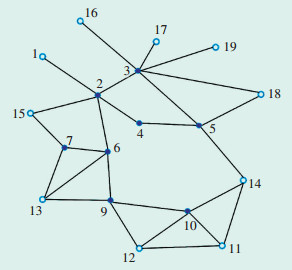
在图 5的规划基础上,假设经过预测发现站点8的负荷近几年内会超过规定阈值,则图 3高速公路待选站点拓扑图更新为图 6,可重新利用Pearto蚁群算法规划起点到终点的站点分布路线。
|
图 6 高速公路待选站点拓扑图 |
本文以多目标电动汽车充电站规划为研究对象,对电动汽车规划的经济性和便利性进行了研究。依据负荷预测数据,利用Pareto蚁群算法对电动汽车充电站进行扩展,最后通过19个站点验证了建立的规划模型的正确性。然而,由于负荷预测训练数据不足,导致预测结果不够准确,在未来的研究中将对该部分不足进行改进。
| [1] |
Shojaabadi S, Abapour S, Abapour M, et al. Optimal planning of plug-in hybrid electric vehicle charging station in distribution network considering demand response programs and uncertainties[J]. Iet Generation Transmission & Distribution, 2016, 10(13): 3330-3340. |
| [2] |
Toregas C, Swain R, ReVelle C, et al. The location of emergency service facilities[J]. Operations Research, 1971, 19(6): 1363-1373. DOI:10.1287/opre.19.6.1363 |
| [3] |
高亚静, 郭艳东, 李天天. 城市电动汽车充电站两步优化选址方法[J]. 中国电力, 2013, 46(8): 143-147. DOI:10.3969/j.issn.1004-9649.2013.08.029 |
| [4] |
Current J.R, ReVelle C.S, Cohon J.L. The maximum covering shortest path problem:amultiobjective network design and routing formulation[J]. European Journal of Operational Research, 2005, 21(2): 189-199. |
| [5] |
刘志鹏, 文福拴, 薛禹胜, 等. 电动汽车充电站的最优选址和定容[J]. 电力系统自动化, 2012, 36(3): 54-59. |
| [6] |
张争辉.电动汽车充电站规划方法研究[D].长沙: 湖南大学, 2015.
|
| [7] |
赵书强, 李志伟. 基于差分进化粒子群算法的城市电动汽车充电站最优规划[J]. 华北电力大学学报(自然科学版), 2015, 42(2): 1-7. DOI:10.3969/j.ISSN.1007-2691.2015.02.01 |
| [8] |
闫天泽, 邱晓燕, 刘延博, 等. 基于引入模拟退火思想的改进粒子群算法的电动汽车充电站最优规划[J]. 电测与仪表, 2017, 54(6): 11-16. DOI:10.3969/j.issn.1001-1390.2017.06.003 |
| [9] |
杨波, 陈卫, 文明浩, 等. 电动汽车充电站的概率负荷建模[J]. 电力系统自动化, 2014, 38(16): 67-73. DOI:10.7500/AEPS20131027001 |
| [10] |
崔和瑞, 彭旭. 基于ARIMAX模型的夏季短期电力负荷预测[J]. 电力系统保护与控制, 2015, 43(4): 108-114. |
| [11] |
M. Hübner, Zhao L, Mirbach T, et al. Impact of large-scale electric vehicle application on power supply[C]. Electrical Power &Energy Conference.Montreal: IEEE, 2009: 1-6.
|
| [12] |
张洪财, 胡泽春, 宋永华, 等. 考虑时空分布的电动汽车充电站负荷预测方法[J]. 电力系统自动化, 2014, 38(1): 13-20. |
| [13] |
杨少兵, 吴命利, 姜久春, 等. 电动汽车负荷建模方法[J]. 电网技术, 2013, 37(5): 1190-1195. |
| [14] |
段海滨, 王道波, 朱家强, 等. 蚁群算法理论及应用研究的进展[J]. 控制与决策, 2004, 19(12): 1321-1326. DOI:10.3321/j.issn:1001-0920.2004.12.001 |
| [15] |
Buscema M. Back propagation neural networks[J]. Substance use & misuse, 1998, 33(2): 233-270. |
| [16] |
Goh A T C. Back-propagation neural networks for modeling complex systems[J]. Artificial Intelligence in Engineering, 1995, 9(3): 143-151. DOI:10.1016/0954-1810(94)00011-S |
| [17] |
Heermann P D, Khazenie N. Classification of multispectral remote sensing data using a back-propagation neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(1): 81-88. DOI:10.1109/36.124218 |
 2019, Vol. 37
2019, Vol. 37