汽轮机旁路温度控制系统通过调节旁路减温水流量来控制旁路蒸汽温度。高旁减温水具有防止高旁超温、控制启动过程中冷再入口蒸汽温度的作用; 低旁的出口接至凝汽器, 故低旁的喷水应将低旁的排汽湿度控制到与汽轮机的排汽湿度相当[1]。因此旁路的减温水控制需要良好的快速响应性、稳定性及控制精度。
目前, 实际应用中的旁路温度控制系统主要采用以适当系数等比例缩小的旁路阀开度信号为前馈的温度单闭环控制方式。该方案虽然较易实施, 但控制器参数的调整需要耗费大量时间, 且抗干扰能力较差, 调门动作频繁。西门子公司根据旁路阀前的主、再热蒸汽压力, 温度和旁路阀开度计算需要的减温水量, 由此确定旁路减温水调节阀的开度指令, 旁路减温器后蒸汽温度不参与闭环控制, 该方案采用开环控制, 难以保证系统的抗扰动能力和控制精度。瑞士CCI公司根据焓值计算得到所需减温水流量, 由流量调节器实现减温水流量的闭环控制, 该方案的控制效果较好, 但在旁路系统中, 需要设计减温水流量测点, 增加额外投入, 且控制器的参数调整需要耗费大量时间[2]。本文提出了带精确前馈控制的Smith预值控制方案, 现场应用效果良好。
1 汽轮机旁路温度控制系统结构汽轮机旁路温度控制系统的控制对象具有影响因素多、参数变化幅度大、大延时、大惯性等特点, 因此提高系统抗扰动能力, 在保证系统稳定的基础上, 提高系统响应快速性以及控制精度, 是为保障旁路温度控制系统良好运行需要解决的主要问题。汽轮机旁路温度控制系统框图如图 1所示。
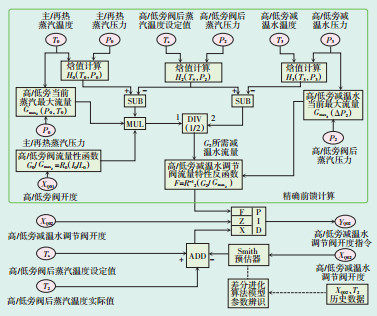
|
图 1 汽轮机旁路温度控制系统框图 |
根据旁路阀前蒸汽压力、温度计算蒸汽焓值, 由旁路阀开度、主蒸汽和再热蒸汽压力、温度及旁路阀的阀体设备参数等得到旁路的蒸汽流量; 结合设置的旁路阀后温度、实际压力, 减温水的温度、压力及减温水调节阀的阀体设备参数等计算所需的减温水流量; 再根据减温水调节阀的流量特性, 将所需减温水量折算为调阀开度, 作为旁路温度控制系统的精确前馈信号, 对主要扰动量进行动态补偿。
以旁路阀后蒸汽温度为被控量进行闭环控制, 采用改进差分进化算法, 利用大量实际运行数据对旁路减温水开度与旁路阀后蒸汽温度的一阶惯性带时滞模型进行参数辨识, 建立较为精确的控制对象数学模型, 依据该模型采用Smith预估器调整控制器参数。
2 汽轮机旁路温度控制精确前馈除启动初期以外, 高/低压旁路阀后蒸汽压力与阀前蒸汽压力之比均小于过热蒸汽临界压比0.546, 蒸汽在高/低旁阀后处于临界流动状态, 所以在阀前压力为P0, 蒸汽温度为T0时高/低旁阀全开时的流量Gmax为:
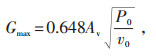
|
(1) |
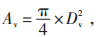
|
(2) |
式中Av-高/低旁阀全开时的流通面积, m2;
Dv-高/低旁阀的阀体通径, 通过阀门清册或就地考察获得, m;
P0-高/低旁阀前蒸汽压力, MPa;
v0-高/低旁阀前蒸汽比容初参数, 可以通过阀前蒸汽压力P0与蒸汽温度T0查看蒸汽参数表获得, m3/kg。
将被控介质流过阀门的相对流量与阀门的相对开度(相对位移)间的关系定义为调节阀的流量特性(其对控制系统的调节品质有很大影响), 可以通过公式(3)表示:
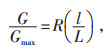
|
(3) |
式中G-在相对开度即开度反馈为l/L且全开流量为Gmax时的流量, kg/h;
l-开度行程, m;
L-全开行程, m。
调节阀的流量特性不仅与阀门的结构和开度有关, 还与阀前后的压差有关, 必须分开讨论。调节阀前后压差固定时得到的流量特性称为固有流量特性, 其取决于阀芯的形状。所以当阀门确定, 不考虑阀芯磨损以及设备故障等情况时, 调节阀的固有流量特性是确定的。实际使用时, 调节阀装在具有阻力的管道系统中, 管道对流体的阻力随流量而变化, 阀前后压差也是变化的, 这时流量特性会发生畸变, 畸变后的流量特性称为调节阀的工作流量特性[3-4]。由于高/低旁阀减温水控制系统采用闭环控制, 且本文利用参数辨识技术和预估控制对闭环控制进行了优化, 即使流量特性函数与实际应用存在一定的偏差, 也能在实际控制时修正, 所以本文采用的调节阀流量特性均为固有流量特性。
综上所述, 根据式(1)-(3)可以得到阀前蒸汽压力为P0、蒸汽温度为T0时高/低旁阀的蒸汽流量:
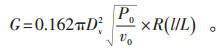
|
(4) |
在不考虑热量损失等因素的影响时, 高/低旁减温器前后的能量是守恒的。当高/低旁阀前压力、温度为P0和T0, 高/低旁减温水压力、温度分别为P3、T3, 高/低旁阀后压力为P2时, 设定温度为Ts所需要的减温水流量G2为:
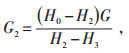
|
(5) |
式中H0-高/低旁阀前压力为P0、温度为T0时的蒸汽焓值, kJ/kg;
H2-高/低旁阀后压力为P2、设定温度为Ts时的蒸汽焓值, kJ/kg;
H3-高/低旁减温水压力为P3、温度为T3时的减温水焓值, kJ/kg。
高/低旁减温水调节阀的阀体, 对于高/低旁减温水具有节流作用, 所以当减温水调节阀全开时, 减温水流量Gmax2可以近似计算为:
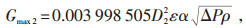
|
(6) |
式中D2-高/低旁减温水调节阀的阀体通径, 通过阀门清册或就地考察获得, m;
ε-流量系数, 可近似为1;
α-可膨胀系数, 可近似为1;
ΔP-减温水调节阀前后差压, MPa;
ρ-减温水密度, kg/m3。
根据公式(3)、(5), 所需要减温水流量为G2时, 可得减温水调门开度为:
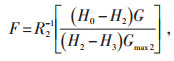
|
(7) |
其中, R2-1为高/低旁减温水调节阀固有流量特性的反函数, 开度F即精确前馈控制的前馈量。
3 基于参数辨识的Smith预估控制 3.1 Smith预估控制采用精确前馈控制虽然能够快速有效地对扰动量(旁路调节阀开度等)进行补偿, 但被控过程控制通道(旁路减温水调门开度-旁路阀后蒸汽温度)本身就是1个典型的大迟延、大惯性环节, 尤其纯迟延特性会影响系统的稳定性, 降低精确前馈的调节效果。当控制对象模型准确时, Smith预估补偿控制可以有效地改善具有大延迟特性系统的控制品质, 因其具有调节时间短、超调量小、鲁棒性好等优点被广泛应用[5]。Smith预估器补偿原理如图 2所示。
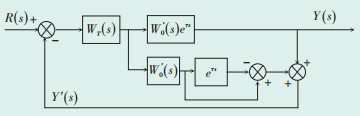
|
图 2 Smith预估器补偿原理图 |
从图 2可以推出系统的闭环传递函数为:
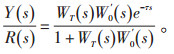
|
(8) |
由公式(8)可见, 对于随动控制经预估补偿, 其特征方程中已消去了e-τs项, 即消除了纯迟延对系统控制品质的不利影响。至于分子之中的e-τs仅仅将系统控制过程曲线在时间轴上推迟了1个τ, 所以预补偿完全补偿了纯迟延对过程的不利影响。控制品质和被控过程与具有无纯迟延环节相同被控对象的系统完全相同。
3.2 基于差分进化算法的参数辨识Smith预估器补偿效果与模型建立的准确性密切相关, 对象模型准确时, 控制效果理想, 否则控制效果不佳甚至导致系统失稳。本文采用参数辨识的方法对旁路减温水调节阀开度XQ02(s)与旁路阀后蒸汽温度T2(s)关系进行建模。根据工程经验及以往研究, 将其传递函数定义为:
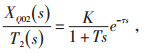
|
(9) |
式中K-比例系数;
T-时间常数, s。
采集旁路减温水调节阀开度及旁路阀后蒸汽温度实际数据, 利用差分进化算法对其数学模型进行参数辨识, 建立准确的模型, 提高Smith预估器的补偿效果。差分进化算法搜索速度快、鲁棒性好, 被广泛应用于约束优化问题上, 对参数辨识也比同类算法具有优越性, 其主要优点可以总结为:待定参数少, 不易陷入局部最优及收敛速度快等[6]。
以实际旁路减温水调节阀开度下辨识模型输出值和对应的旁路阀后蒸汽温度实际值的均方差构造目标函数(即适应度)。设待定参数x=[x1, x2, x3] (对应模型中的3个待定参数K, T, τ)种群中第i个个体用xi=[xi1, xi2, xi3]表示。差分进化算法参数辨识步骤如下。
(1) 生成初始群体, 随机产生满足约束条件的个体, 根据式(10)生成初始种群:
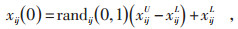
|
(10) |
其中, xijU和xijL是第i个染色体的上下界, randij(0, 1)是[0, 1]的随机数。
(2) 变异操作, 从种群中随机选取2个不同的个体xp1和xp2, 根据公式(11)对第k代种群个体实现变异, 生成变异个体vij(k+1):
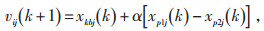
|
(11) |
其中, xp1j(k)-xp2j (k)为差异化向量, 此差分操作是差分进化算法的关键; α为缩放因子; p1和p2为随机整数, xkbj (k)是第k代种群中适应度最好的个体。如此改进, 可以借助最好个体的信息加快收敛速度, 减小运算量。
(3) 交叉操作, 根据式(12)进行交叉操作, 以此增加种群的多样性:
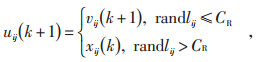
|
(12) |
其中, randlij是[0, 1]的随机数, CR∈[0, 1], 为交叉概率。
(4) 选择操作, 根据式(13)进行选择操作, 确定个体能否成为下一代种群成员:
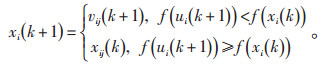
|
(13) |
根据式(14)选出最优个体:
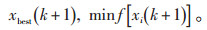
|
(14) |
转步骤(2)重复上述操作, 直到达到进化代数, 最优个体即为参数辨识最终结果。
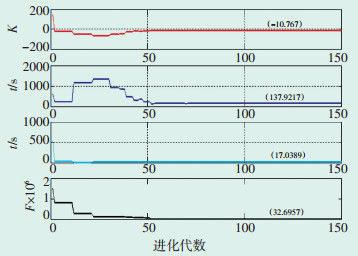
3.3 控制对象建模为了建立符合实际的旁路减温水调节阀开度-旁路阀后蒸汽温度关系数学模型, 本文针对某电厂350 MW机组, 按1 s间隔在未投入自动期间(开环)且低旁阀维持一定开度不变的情况下获取实际运行数据样本[7-9]。为了提高数据质量, 利用小波滤波方法对数据进行平滑处理。采用上述改进差分进化算法对旁路减温水调节阀开度-旁路阀后蒸汽温度模型进行参数辨识, 建立准确的数学模型[10]。高旁温度控制对象数学模型参数辨识结果见图 3。在进化代数达到9后, 所有参数均收敛, 且适应度F由1.513×104降低至32.6957, 说明通过改进差分进化算法辨识未知参数的数学模型与实际模型非常接近。高旁减温水调节阀开度-高旁阀后蒸汽温度模型为:
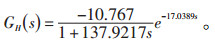
|
(15) |
|
图 3 高旁温度控制对象数学模型参数辨识结果 |
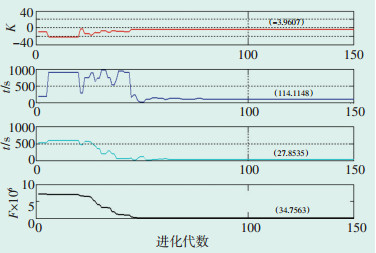
低旁温度控制对象数学模型参数辨识结果见图 4。在进化代数达到115之后, 所有参数均收敛, 且适应度F由7.136×106降低至34.7563, 说明通过差分进化算法辨识未知参数的数学模型与实际模型非常接近。低旁减温水调节阀开度-低旁阀后蒸汽温度模型为:
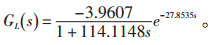
|
(16) |
|
图 4 低旁温度控制对象数学模型参数辨识结果 |
在Simulink环境下建立控制模型, 对本文提出的旁路减温水控制方法进行验证。
通过定值扰动和外部扰动的方式, 验证控制方法[11-12]。采用3种高旁减温水温度控制方案。
(1) 方案1:传统单回路PID控制;
(2) 方案2:在方案一的基础上加入前馈补偿控制;
(3) 方案3:在方案2的基础上加入Smith预估控制。
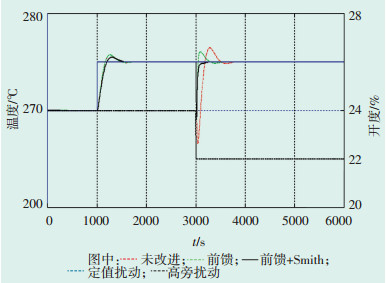
3种方案中PID参数均设为Kp=0.098, Ki= 0.0027, 在1000 s时将高旁阀后蒸汽温度设定值由270℃提高为275℃, 3000 s时引入高旁阀开度扰动, 高旁阀开度由24%减小为22%;高旁减温水温度控制系统仿真结果如图 5所示。在1000 s加入5℃的定值扰动后, 方案1、方案2的超调量比方案3的超调量要大, 在3000 s加入2%高旁开度扰动后, 方案1的超调量和稳定时间均高于方案2, 而方案3的超调量和稳定时间均小于方案2。由此可见, 利用前馈校正作用及时补偿高旁开度带来的扰动, 而且利用Smith预估器的补偿作用消除了控制通道的滞后影响, 使高旁减温水系统无论在定值扰动还是高旁开度扰动下更加稳定; 在实际应用中由于引入了改进差分进化算法辨识控制对象模型, 极大地提高了模型精度, 提高了Smith预估器的补偿准确度[13-16]。
|
图 5 高旁减温水温度控制系统仿真结果 |
低旁减温水控制系统亦采用上述3种方案控制进行对比, 3种方案中PID参数均设为Kp=0.025, Ki= 0.0088, 在1000 s时将低旁阀后蒸汽温度设定值由70℃提高至80℃, 3000 s时引入低旁阀开度扰动, 低旁阀开度由10%增加为12%;低旁减温水控制系统仿真结果见如图 6。上述高旁温度控制系统仿真分析结果在高旁温度控制系统仿真结果中亦适用。
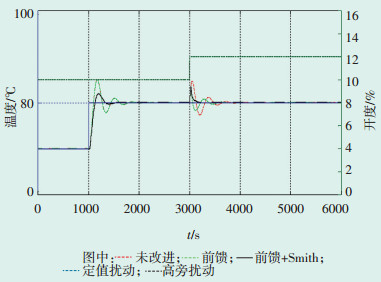
|
图 6 低旁温度控制系统仿真结果 |
某电厂350 MW机组采用高低压二级串联旁路, 旁路容量为40% B-MCR电动旁路, 高压旁路的减温水取自给水系统的给水泵出口母管, 低压旁路的减温水取自凝结水泵出口的凝结水管道。主要调节阀通径参数如表 1所示。
| 表 1 主要调节阀门通径 |
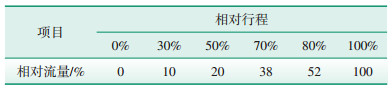
高旁调节阀、高旁减温水调节阀固有流量特性均为等百分比特性且相同, 如表 2、表 3所示。
| 表 2 高旁调节阀固有流量特性 |
| 表 3 高旁减温水调节阀固有流量特性 |
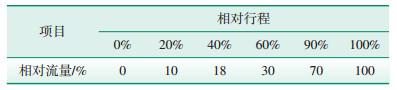
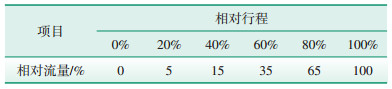
低旁调节阀及低旁减温水调节阀固有流量特性均为等百分比特性, 如表 4、表 5所示。
| 表 4 低旁调节阀固有流量特性 |
| 表 5 低旁减温水调节阀固有流量特性 |
根据以上主要参数, 依据本文提出的旁路温度控制优化方法, 在组态中搭建了相关控制逻辑。机组2次启动过程中, 高、低旁调节阀均在手动的情况下, 高、低旁温度控制系统实际运行曲线如图 7、8所示。从图 7可以看出, 高旁减温水温度设定值为276℃, 在高旁调节阀开度大幅度变化的情况下, 始终维持着高旁阀后温度的稳定, 动态最大偏差为3.7℃, 静态最大偏差为0.5℃。图 8中, 低旁减温水温度设定值为85℃, 在低旁调节阀开度大幅度变化的情况下, 始终维持着低旁阀后温度的稳定, 动态最大偏差为6.8℃, 静态最大偏差为1.2℃。
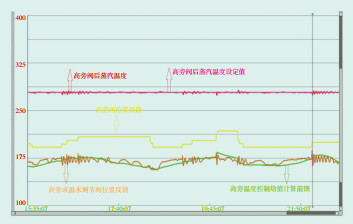
|
图 7 高旁温度控制系统优化后实际运行曲线 |
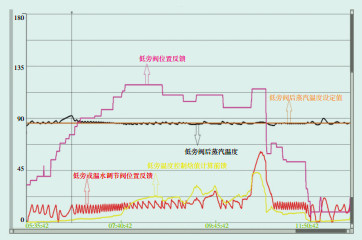
|
图 8 低旁温度控制系统优化后实际运行曲线 |
现场实际应用效果表明, 本文提出的优化控制方法能够满足机组实际控制需求, 工程上切实可行。
6 结论本文提出的带精确前馈控制结合基于差分进化算法的参数辨识建模Smith预估控制方案, 在旁路温度控制系统中具有鲁棒性好、调节速度快、抗扰动能力强等特点, 尤其是针对旁路调节阀开度的扰动具有很好的调节效果, 并由此得出以下结论:
(1) 研究结果对高、低旁路温度控制系统具有很好的调节效果, 该方法完全可以由现有组态逻辑搭建实现, 工程上切实可行。
(2) 研究结果的适用对象不局限于旁路温度控制系统, 完全可以应用于其他大延迟、大惯性、大扰动系统。
| [1] |
冯伟忠. 外高桥电厂二期900 MW汽轮机的技术特点[J]. 热力发电, 2003(6): 2-5. DOI:10.3969/j.issn.1002-3364.2003.06.001 |
| [2] |
冯伟忠. 1000 MW级火电机组旁路系统作用及配置[J]. 中国电力, 2005, 38(8): 53-56. DOI:10.3969/j.issn.1004-9649.2005.08.014 |
| [3] |
彭领新. 汽轮机旁路系统设计[J]. 电力建设, 2000, 21(7): 21-25. DOI:10.3969/j.issn.1000-7229.2000.07.007 |
| [4] |
聂雨, 张燕平, 黄树红. 汽轮机旁路系统仿真建模[J]. 热能动力工程, 2013, 28(4): 336-340. |
| [5] |
韩剑辉, 张维波. 汽轮机旁路系统控制方式设计[J]. 哈尔滨理工大学学报, 2007(12): 23-26. |
| [6] |
杨培成, 周丽. 低压旁路温度典型控制策略对比分析及优化[J]. 热力发电, 2010, 39(7): 57-61. DOI:10.3969/j.issn.1002-3364.2010.07.057 |
| [7] |
吴国熙. 调节阀的使用与维护[M]. 北京: 化学工业出版社, 1999: 97-121.
|
| [8] |
明赐东. 调节阀计算、选型、使用[M]. 成都: 成都科技大学出版社, 1999: 11-32.
|
| [9] |
OSHIMA Shigeru, LEINO Timo. Experimental study on cavitation in water hydraulic[J]. Transaction of The Japan Fluid Power System Society, 2002, 33(2): 29-35. DOI:10.5739/jfps.33.29 |
| [10] |
何衍庆. 控制阀工程设计及应用[M]. 北京: 化学工业出版社, 2005: 39-188.
|
| [11] |
宋年年, 熊叔燕, 安舞. 带负荷前馈的Smith预估串级汽温控制系统仿真研究[J]. 计算机仿真, 1996, 13(2): 25-29. |
| [12] |
张君, 邓菲, 翟永杰. 改进的Smith串级主汽温控制仿真研究[J]. 计算机仿真, 2016, 33(5): 148-151. DOI:10.3969/j.issn.1006-9348.2016.05.031 |
| [13] |
黄宇, 韩璞, 李永玲. 主汽温系统模糊自适应内模控制[J]. 中国电机工程学报, 2008, 28(23): 93-98. |
| [14] |
余洁, 杨平. 基于差分进化算法的SCR喷氨量模型参数辨识[J]. 现代制造, 2017(24): 106-109. |
| [15] |
熊伟丽, 许文强, 徐保国. 基于差分进化算法的Wiener模型辨识[J]. 自动化技术与应用, 2012, 19(12): 1-5. |
| [16] |
张平, 苑明哲, 王宏. 大时滞系统自适应模糊Smith控制[J]. 计算机仿真, 2006, 23(9): 87-90. DOI:10.3969/j.issn.1006-9348.2006.09.024 |
 2019, Vol. 37
2019, Vol. 37