近年来,在政府政策的大力支持下,电动汽车行业发展迅速,我国已经成为电动汽车的产销大国。电动汽车的推广受制于充电设施的发展,根据中国电动汽车充电基础设施促进联盟提供的数据,截至2016年12月,全球范围内的车桩保有量比例为7:1[1],远不能满足充电需求。2015年10月国务院办公厅发布的《关于加快电动汽车充电设施建设的指导意见》及四部委发布的《电动汽车充电基础设施发展指南》(2015—2020),我国将新增集中式充换电站超过1.2万座,分散式充电桩超过480万个,以此来弥补充电设施数量上的差距。但是目前我国主要以建设集中式充电站为主,对于分散式充电设施的建设速度相对较慢,对于未来新增的大量分散式充电设施的优化规划问题,本文提出了二次规划模型。
1 电动汽车充电设施研究现状目前对于电动汽车充电设施的研究大部分是针对充电站的规划。电动汽车充电负荷的准确预测是充电设施规划的基础。文献[2]根据私家车的行驶统计数据,分析了充电功率需求。文献[3]在负荷预测中综合考虑了私家车、公交车、出租车等不同类型汽车的行驶特性,计算出了充电负荷的时间分布。文献[4]从时间和空间2个方面分析了充电需求。文献[5]采用车流量信息模拟各个充电站充电需求。文献[6]基于不同类型用地的停车需求对充电负荷进行时空分布预测。文献[7]提出将土地性质转化为用电负荷,得出充电负荷的空间分布。在选址和定容方面,文献[8]兼顾充电站运营者和电动汽车用户双方利益,提出一种基于全社会成本最小化的充电站规划布局优选模型。文献[9]以经济效益最大化为目标对充电站的地址及容量进行规划。文献[10]基于计算几何方法以年运行收益最大对充电站进行规划。文献[11]提出了以投资运营商获得的净现值收益最大为目标,设计了LCC的优化规划模型。
以上研究主要以集中式充电站为主,在理论上对于分散式充电设施的研究较少。文献[12]分析了充电模式的选择原则,提出未来充电设施的建设应以分散充电设施为主。文献[13]提出了分散式充电桩与电动汽车配比度的分析计算方法,模型以用户可接受的最低剩余电池容量Cx为变量,计算充电需求概率。
除了对分散式充电设施研究较少,目前充电设施的规划研究也较少考虑已建的充电设施,造成原有充电站与新建充电设施规划不协调。本文在充分考虑已有充电设施基础上,提出电动汽车分散式充电设施二次规划模型。
2 电动汽车充电设施类型选择目前中国城市电动汽车充电基础设施主要包括各类集中式充换电站和分散式充电桩。我国在充电站的定位上与国外不同,美国主要以慢充为主,快充作为补充以应急,而我国在电动汽车发展的初期主要以快充为主,以充电站作为能量补给。然而对于城市核心地区来说,应以分散式充电设施为主,原因主要有以下几个方面:
(1)在建设用地方面,分散式充电设施不需单独征地,在小区停车场、办公楼停车场等停车区域都可以建设,可充分利用空间资源;
(2)在电网影响方面,分散充电设施主要是由慢速充电桩组成,充电电流约15 A,对电网的冲击比较小;
(3)投资方面,分散式充电设施依靠停车场建设,不存在征地费用问题,并且对于技术要求较低,容易实现,投资小。
3 分散式充电设施需求量预测分散式充电设施包括私人充电桩和公共充电桩,服务对象有私家车、出租车和公务车。私人充电桩的建设位置固定,车桩按照1:1配置,不需要规划。公共充电桩建设场所有居民区、办公区、商业区和休闲娱乐区等功能区的停车位。在居民区的公共停车位建设充电桩存在安全和便利问题,因此只对服务于私家车的其他公共充电桩进行数量预测。
3.1 充电概率模型用户决定在目的地是否充电取决于Cx,因此本文在已知用户居住地到目的地距离基础上,通过计算Cx得到充电概率。在分析时做如下假设:
(1)电动汽车每天起始地点为家庭;
(2)用户从家庭出发只有一个目的地,且往返里程相同;
(3)行驶里程与电池容量消耗呈线性关系;
(4)城市核心地区用户行驶里程短,每天最多只充1次电;
(5)当电池容量大于90%时用户不会充电,小于30%时肯定充电。
从家庭出发时的电池容量CSOC受用户的充电习惯以及日行驶距离等因素影响,假设满足[0.5,1]均匀分布。用户从住宅区到目的地往返消耗的电池容量为Cc=2d/D,其中d为用户到达目的地的平均行驶里程,D为续驶里程水平,一般取100 km。用户往返住宅区时的剩余电池容量Cx=CSOC-Cc,则用户在目的地的充电概率函数p(x)为[14-15]:
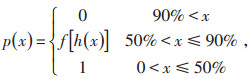
|
(1) |
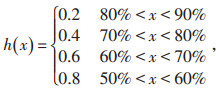
|
(2) |
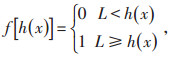
|
(3) |
其中,f[h(x)]是剩余电池容量Cx的函数,其数值决定充电与否,取值为0和1,数字L随机产生,满足[0, 1]均匀分布。
3.2 停车需求量模型城市用地一般分为居住用地、行政办公用地、商业金融用地、文化娱乐用地,功能区的停车需求量受规划区的土地利用性质、人口、经济水平、发展战略等因素影响。结合多方面因素,提出每个功能区的停车需求量计算模型如公式(4):
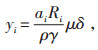
|
(4) |
式中 yi—i功能区高峰时刻的停车需求量;
ai—i功能区的停车需求生成率;
Ri—i功能区用地面积;
ρ—高峰时间周转率;
γ—高峰时间利用率;
μ—价格因素的影响率;
δ—服务水平的影响率。
参数的具体取值原则参考文献[16]。
3.3 充电设施需求量充电设施需求量计算公式如公式(5):
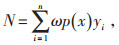
|
(5) |
式中 N—规划区电动汽车充电设施需求量;
ω—规划区电动汽车的渗透率,%;
n—功能区个数。
电动汽车的渗透率需要根据规划区未来几年电动汽车的发展设定,一般按照适度超前的原则。最终规划区域实际安装的充电桩数量取为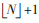
在市场的竞争下未来会有更多的社会资本融入充电设施建设投资中,成本问题至关重要。目前一些城市如北京、深圳等已建有大量的充电站,在新增充电桩规划时应避免服务范围内重复建设,造成资源和成本的浪费。充电站有自己的覆盖范围,除此之外的范围由新建的充电设施覆盖。但资源有限,可能并不能覆盖所有需求点,此时引用最大覆盖选址模型可以尽可能多地满足需求。在选址的基础上以综合收益最大为目标确定功能区内新建的充电桩数量。
4.1 二次规划选址模型当充电设施数量确定后,在特定距离、给定建设数量条件下,可能无法满足所有需求点的充电需求,因此建立最大覆盖模型,见公式(6)和(7)[17-18],可以最大化满足需求。
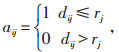
|
(6) |
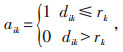
|
(7) |
其中,dij、dik为需求点到候选地址和充电站距离;rj、rk分别为新建充电桩和充电站的覆盖半径;aij、aik为1时表示需求点i分别可以到新建设施和充电站充电,若需求点同时在2种设施范围内,选择充电站充电,此时aij=0、aik=1。
建立最大覆盖模型的目标是获得最大需求覆盖量R:
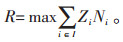
|
(8) |
其约束条件见公式(9)—(12):
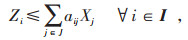
|
(9) |
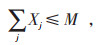
|
(10) |
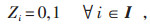
|
(11) |
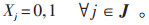
|
(12) |
其中,i为需求点,I为需求点集,i∈I;j为候选点,J为候选点集,j∈J。当需求点i被充电设施覆盖时,Zi为1,否则为0;Ni为需求点i的需求量;Xj取值为1表示在候选点j设立充电桩,否则为0;M为规划区候选点个数。
4.2 二次规划定容模型 4.2.1 目标函数经济化最优目标函数见公式(13):
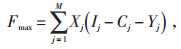
|
(13) |
式中 Fmax—j功能区最优收入;
Ij—j功能区内充电桩充电费用年收入;
Cj—j功能区充电桩建设投资费用;
Yj—j功能区内充电桩的运行费用。
(1)j功能区内充电桩充电费用年收入计算公式为:
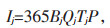
|
(14) |
式中 Bj—j功能区建设充电桩数量;
Qj—j功能区充电收费价格;
Tj—j功能区内充电桩平均日利用小时数;
P—充电桩充电功率。
(2)j功能区充电桩建设投资费用计算公式为:
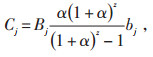
|
(15) |
式中 α—贴现率;
z—运行年限;
bj—单个充电桩建设投资费用。
(3)充电桩的运行维护费用包括充电桩的日常维护费用、材料成本和管理费用等(与停车场内充电桩数量以及场地类型有关)。投运至目标年的运行费用折算为初期的投资费用,设折算系数为η,则j功能区内充电桩的运行费用为:
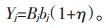
|
(16) |
经济化最优目标函数约束条件见公式(17)—(20)。
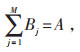
|
(17) |
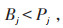
|
(18) |
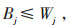
|
(19) |
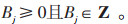
|
(20) |
式中 A—新建充电桩总数;
Wj—j功能区充电设施需求量;
Pj—j功能区内停车位数。
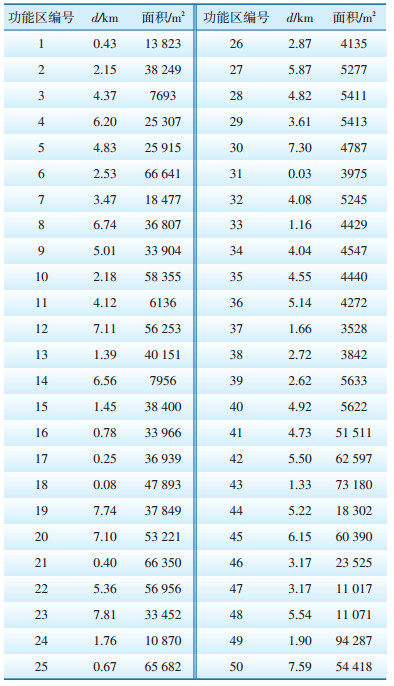
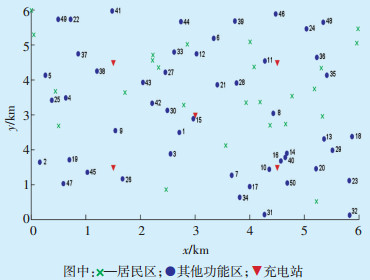
5 算例分析根据上述模型对城市核心地区2020年分散式充电设施进行规划。该城市核心规划区有75个功能区,其中居民区25个,商业区25个,办公区15个,休闲区10个,其位置在平面坐标中随机产生。已经建设的充电站有5个,图 1为平面位置图,其中,编号1—25为商业区,26—40为办公区,41—50为休闲区。进行优化配置计算时图 1中编号1—50功能区所对应的充电设施需求预测具体数据如表 1所示。
|
图 1 各功能区平面位置图 |
| 表 1 需求预测具体数据 |
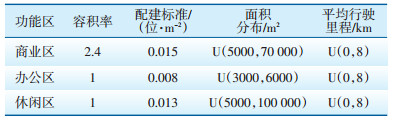
模型仅针对除居民区以外的功能区电动汽车充电设施进行规划,2020年规划区电动私家车参数ρ=1.3,γ=100%,μ=70%,δ=1,到目标规划年其渗透率ω预计为5%。不同类型功能区停车位建设标准、容积率参考文献[4],需求预测相关参数如表 2所示。根据表 1中充电需求预测具体数据以及公式(1)—(5)可得出规划区各功能区充电桩的需求量,计算得出总需求量为820个。
| 表 2 需求预测相关参数 |
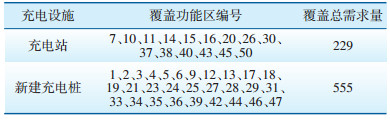
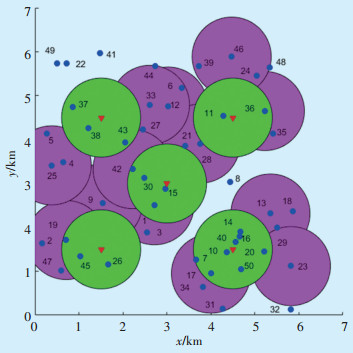
初期安装充电桩的功能区候选站址个数为20个,站址数量限制为15个。经过实际调查,初步选取功能区1、6、9、12、13、17、19、22、23、24、25、27、28、29、33、36、41、42、46、47作为新建设施的候选站址。充电设施的覆盖半径为0.9 km,以最大覆盖需求量为目标,确定候选站址为1、9、12、13、17、19、23、25、28、33、36、42、46。根据3.1节,同时在2种设施服务范围时,认为顾客选择充电站。然而由于这些功能区为新建充电设施地址,因此认为顾客会选择在功能区的充电桩充电。图 2展示了充电站以及各新建充电设施具体的服务对象,表 3为充电站以及新建充电设施总覆盖量需求统计情况。可以看出,由于资源和候选站址数量有限,功能区8、22、32、41、48、49并没有在充电设施的服务范围,但模型实现了最大的需求覆盖量。
|
图 2 充电设施服务对象 |
| 表 3 充电设施覆盖需求统计 |
功能区新建充电桩的平均日利用小时数既与该功能区所覆盖的充电需求量成正比关系,又和安装的充电桩数量成反比。需要注意的是,如果需求点在多个新建充电设施服务范围,需求点与某个新建充电设施位置重合,则属于该充电设施的覆盖需求;若不重合,则可分配给任何1个充电设施。
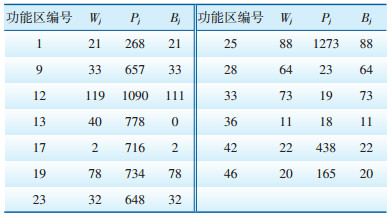
以常规充电桩为例,功率3.5 kW,商业区、办公区、休闲区安装单价分别为1800元、1700元、1600元,收费标准分别为1.8元/kWh、1.2元/kWh、1.5元/ kWh。参数α=0.1,z=20,η=0.2。功能区充电设施建设数量的优化分配结果有多种,经计算,最大收益皆为8 771 009元,表 4为其中一种分配结果。
| 表 4 优化分配结果 |
城市核心地区电动汽车充电设施的建设需要考虑很多因素,本文对充电设施类型综合分析后得出城市核心地区应以分散式为主。通过二次规划模型将新增的充电设施在已建有充电站的地区合理地进行布局,模型在资源有限条件下,实现了服务需求量最大化,也达到了经济型最优的目标,充分利用了资源,可供城市核心地区电动汽车充电设施的规划借鉴。
| [1] |
王寅飞, 郑泰山, 李鹏, 等. 新能源汽车能量补充模式分析与探讨[J]. 机电工程技术, 2017, 46(3): 19-23. DOI:10.3969/j.issn.1009-9492.2017.03.005 |
| [2] |
田立亭, 史双龙, 贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术, 2010, 34(11): 126-130. |
| [3] |
罗卓伟, 胡泽春, 宋永华, 等. 电动汽车充电负荷计算方法[J]. 电力系统自动化, 2011, 35(14): 36-42. |
| [4] |
张洪财, 胡泽春, 宋永华, 等. 考虑时空分布的电动汽车充电负荷预测方法[J]. 电力系统自动化, 2014, 38(1): 13-20. |
| [5] |
葛少云, 冯亮, 刘洪, 等. 考虑车流信息与配电网络容量约束的充电站规划[J]. 电网技术, 2013, 37(3): 582-589. |
| [6] |
寇凌峰, 刘自发, 周欢. 区域电动汽车充电站规划的模型与算法[J]. 现代电力, 2010, 27(4): 44-48. DOI:10.3969/j.issn.1007-2322.2010.04.010 |
| [7] |
张艳娟, 苏小林, 闫晓霞, 等. 基于电动汽车时空特性的充电负荷预测[J]. 电力建设, 2015, 36(7): 75-82. DOI:10.3969/j.issn.1000-7229.2015.07.010 |
| [8] |
葛少云, 冯亮, 刘洪, 等. 电动汽车充电站规划布局与选址方案的优化方法[J]. 中国电力, 2012, 45(11): 96-101. DOI:10.3969/j.issn.1004-9649.2012.11.021 |
| [9] |
吴春阳, 黎灿兵, 杜力, 等. 电动汽车充电设施规划方法[J]. 电力系统自动化, 2010, 34(24): 36-39, 45. |
| [10] |
唐现刚, 刘俊勇, 刘友波, 等. 基于计算几何方法的电动汽车充电站规划[J]. 电力系统自动化, 2012, 36(8): 24-30. |
| [11] |
黄小庆, 杨夯, 陈颉, 等. 基于LCC和量子遗传算法的电动汽车充电站优化规划[J]. 电力系统自动化, 2015, 39(17): 176-182. DOI:10.7500/AEPS20150323009 |
| [12] |
肖湘宁, 温剑锋, 陶顺, 等. 电动汽车充电基础设施规划中若干关键问题的研究与建议[J]. 电工技术学报, 2014, 29(8): 1-10. DOI:10.3969/j.issn.1000-6753.2014.08.001 |
| [13] |
陶顺, 肖湘宁, 温剑锋, 等. 电动汽车分散充电设施配比度分析与计算方法[J]. 电工技术学报, 2014, 29(8): 11-19. DOI:10.3969/j.issn.1000-6753.2014.08.002 |
| [14] |
高赐威, 张亮. 电动汽车充电对电网影响的综述[J]. 电网技术, 2011, 35(2): 127-131. |
| [15] |
葛少云, 李荣, 韩俊, 等. 考虑电动汽出租车随机概率行为特性的充电站规划[J]. 电力系统自动化, 2016, 40(4): 50-58. |
| [16] |
关宏志, 王鑫, 王雪. 停车需求预测方法研究[J]. 北京工业大学学报, 2006(7): 600-604. DOI:10.3969/j.issn.0254-0037.2006.07.006 |
| [17] |
王丹, 马云峰. 竞争与合作设施并存的最大覆盖选址问题[J]. 武汉理工大学学报(信息与管理工程版), 2010, 32(4): 628-631, 635. DOI:10.3963/j.issn.1007-144X.2010.04.030 |
| [18] |
朱鹰屏, 张绪红, 韩新莹. 用于配电网网损优化的电动汽车智能充电调度[J]. 广东电力, 2016, 29(9): 94-97, 103. DOI:10.3969/j.issn.1007-290X.2016.09.019 |
 2018, Vol. 36
2018, Vol. 36