2. 内蒙古超高压供电局, 呼和浩特 010080
2. Inner Mongolia UHV Power Supply Bureau, Hohhot 010080, China
随着工业的快速发展,机动车数量的增多,造成化石能源的过度使用,导致空气质量日益恶化。电动汽车因其节能、环保、零排放的特性,被视为改善城市空气质量的有效手段。但是电动汽车的推广,尤其在寒冷地区仍面临诸多问题。技术层面上,受限于电池容量及性能,在满充状态下,正常航里程仍不足300 km,特别是在高寒地区,受低温环境影响,电池的容量衰减加速,续航里程通常低于200 km,严重降低了电动汽车的竞争力。除京津冀等发达地区外,高寒地区公共充电设施不完善,购置的电动汽车可能面临无处充电的情况,另外消费者对电动汽车的认知及接受度较低等因素都制约了电动汽车在高寒地区的推广。对此认为建设较为完善的城市充电网络可促进北方高寒地区电动汽车的发展。本文利用蒙特卡洛仿真方法模拟区域内电动汽车的运行及充电情况,并对快充与慢充装置的配比进行研究。
1 地区充电负荷预测模拟流程 1.1 充电负荷预测及已有研究存在的不足地区充电负荷预测是通过建立数学模型估算该地区短期(1个典型日)、中长期(通常为6~12个月)充电负荷的变化过程。电动汽车充电负荷类似于居民生活用电负荷,具有较大的随机性。充电负荷预测通常是通过对群体内单台车辆的充电行为进行仿真,然后收集全部充电行为数据,进而获得地区充电负荷特性。地区充电网络的容量主要取决于该地区的充电负荷。精确掌握区域内典型日的充电负荷特征,可确定充电网络规模及不同充电设施的配比。相关文献已经对利用典型的概率分布分析电动汽车的运行特性进行较为全面的研究。文献[1-2]认为汽车最后行程返回时刻及日行驶里程近似满足正态分布和对数正态分布;文献[3]认为车主充电习惯的不同使得充电过程面临更多的不确定性;文献[4]通过对充电站的流量及工作特性的观察,建立充电站服务模型,以确定快充网络的充电负荷。上述文献试图将电动汽车的日内运行特性通过一种典型分布加以描述。但通过对私家车运行数据的分析可以发现,研究样本规模越大,通过一种典型分布对其进行描述越难。另外上述研究没有将快充及慢充负荷统筹考虑,因此无法形成完整的充电网络配置方案。
1.2 定义变量假设各台电动汽车的充电方式为慢充为主、快充补电,即日内最后一次行驶结束后,采用慢充,而日间如果出现缺电的情况,则快充补电,并引入充电行为不确定性加以修正。不确定性主要体现在车主当日最后一次行驶结束后忘记充电,或者最后一次行驶结束后选择快充等方面。drvlReci为某电动汽车单次行驶记录,其中包含的主要数据项如表 1所示。
| 表 1 1条行驶记录样例 |
对如下变量进行定义。
(1)CSOC:荷电状态,用于描述电池的容量,通常定义为电池的剩余容量Cr与总容量Ct的比值,通过公式(1)计算:
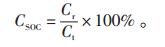
|
(1) |
(2)CSOClimit:电池正常运行所允许的最小CSOC,当CSOC < CSOClimit时,必须及时充电,否则将影响电池的寿命。
(3)ΔCSOCi:第i次行驶导致CSOC的变化量,其中CSOCi为第i次行驶时电池的初始容量。如果第i次行驶里程为Li,电动汽车的理论续航里程为Lmax,同时假设行驶里程与电池容量的变化满足线性关系,则第i次行驶导致的电池容量变化按照公式(2)、公式(3)计算:
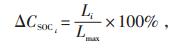
|
(2) |
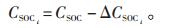
|
(3) |
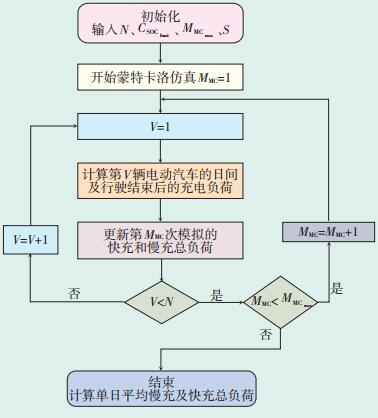
使用蒙特卡洛方法模拟计算区域内充电总负荷的流程如图 1所示。
|
图中:V—具体电动汽车辆数;MMC—具体仿真次数 图 1 蒙特卡洛模拟计算电动汽车充电总负荷流程图 |
输入地区内单日运行的电动汽车总数N;电动汽车需要进行充电的警戒电量CSOClimit,如果一次行驶导致CSOC低于CSOClimit,则必须在行驶前充电;MMCmax(需要进行蒙特卡洛仿真计算的总次数)以及n条单日汽车行驶记录集合S,开始进行蒙特卡洛模拟。
1.3.2 仿真计算阶段结合每台电动汽车的具体行驶情况和电池的SOC确定充电负荷。根据行驶记录计算单辆电动汽车的快充及慢充负荷,主要包含如下步骤:
(1)步骤1:对于第i条行驶记录drvlReci,预估里程可能消耗的电池电量ΔCSOCi;
(2)步骤2:如果ΔCSOCi高于运行允许的最低容量CSOClimit,利用公式(2)(3)将CSOC更新至ΔCSOCi。如果drvlReci不是日内最后一次行驶,则返回步骤1继续处理下1条日内行驶记录;否则进入步骤3快充补电;如果drvlReci是日内最后一次行驶,则进入步骤4。
(3)步骤3:判断第i-1条行驶记录结束时间与第i条行驶记录开始的时间间隔是否大于快充需要的充电时间,如果大于,则在i-1次行驶结束后更新快充总负荷,否则继续回溯到第i-2条数据,直到找到满足快充条件的时间间隔为止,更新CSOC后回到步骤2,重新处理drvlReci;
(4)步骤4:根据CSOC及日内最后一次行驶的结束时间计算慢充负荷。
1.3.3 流程结束本次蒙特卡洛仿真结束后,分别存储本次仿真的快充总负荷及慢充总负荷。当MMC = MMCmax时,计算全部蒙特卡洛仿真的平均快充负荷及慢充负荷。然后依据式(4)确定充电装置的数量。

|
(4) |
其中,NF、NS为快充桩及慢充桩的数量,Pmax f、Pmax s为快充负荷及慢充负荷曲线的峰值,CF、CS为快充桩及慢充桩的额定功率。
2 地区充电设施容量配置结合北方某省会城市“十三五电动汽车规划”给出的应用负荷预测进行容量配置。根据该规划截至2020年,市区电动汽车保有量将达到10 000辆。目前国内尚无完备的电动汽车运行数据,只能使用传统汽车的驾驶信息样本。国内外大部分的相关研究(文献[2-5])均使用美国交通运输部所做的全国家庭出行调查(National Household Travel Survey,NHTS)作为原始数据集样本。最新一期的数据集合NHTS-2009包含约100万条行驶记录,足以覆盖一个中等规模城市单日电动汽车的全部出行特征。同时,结合电动汽车续航里程的限制,过滤掉原始数据集合中单日总里程超过260 km,单程超过180 km的行驶记录。
2.1 不考虑车型差异的负荷估算首先做出如下假设:90%的车辆初始CSOC满足(0.8,1.0)的均匀分布,剩余10%车辆初始CSOC满足(0.3,0.8)的均匀分布。当一次行程可能导致CSOC低于20%警戒值,车主会选择快速充电。充电过程统一采用恒功率充电,快充功率为60 kW,慢充为5 kW;每座充电站均配备6台快充桩。
依据文献[1]的研究,在1个典型日内,有14%的车辆不出行,故从原始数据集中抽取8600个单日行驶记录,得出快充和慢充负荷曲线分别如图 2、图 3所示。
|
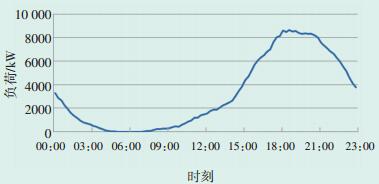
图 2 不考虑车型差异的典型日慢充负荷曲线 |
|
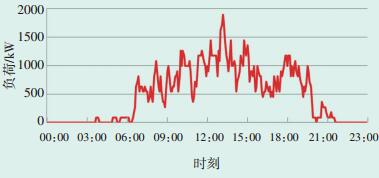
图 3 不考虑车型差异的典型日快充负荷曲线 |
从图 2慢充负荷曲线中可以看出,充电高峰主要集中于16:00—22:00,峰值出现在18:00附近,最大负荷约为8200 kW,则大约需要慢充桩1700台。从图 3快充负荷曲线可以看出,快充没有明显的峰谷特征,最大值出现在13:00附近,负荷约1900 kW,则需要快充桩约33台,据此得到充电设施配置方案如表 2所示。
| 表 2 不考虑车型差异的充电设置配置方案 |
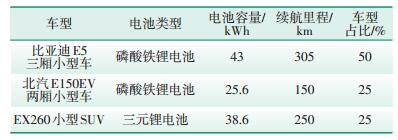
以上仿真计算忽略了车型差异及充电行为不确定性2个因素。本节选取表 3中3款目前市场上主流电动车型,类比同类型传统汽车在该市的保有量,预计其未来占比分别为50%、25%及25%。另外考虑到充电行为具有较大的不确定性,假设单日行驶结束后,有20%的车主选择快充充电,得出快充及慢充的负荷曲线如图 4、图 5所示。
| 表 3 主流电动汽车的动力电池及续航里程参数 |
|
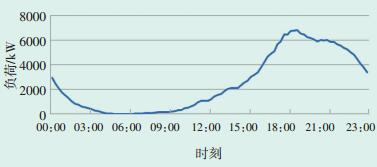
图 4 考虑车型差异及充电行为不确定性的典型日慢充负荷曲线 |
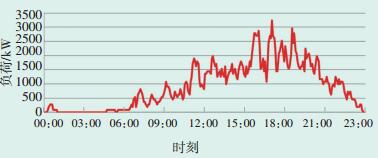
|
图 5 考虑车型差异及充电行为不确定性的典型日快充负荷曲线 |
从图 4慢充负荷曲线中可以看出,充电高峰主要集中于16:00—22:00,峰值出现在18:00—19:00,最大负荷约为6500 kW,因此需要慢充桩约1300台。
从图 5快充负荷曲线可以看出,当日间行程结束后,有20%的车主选择快充方式,快充高峰集中于15:00—19:00,峰值约3250 kW,因此需要快充桩约55台,据此得到充电设施配置方案见表 4。
| 表 4 计及车型差异的充电设置配置方案 |
本文以北方某省会城市2020年10 000辆电动汽车为例,在基于蒙特卡洛仿真的充电负荷建模基础上得出了快充桩及慢充桩的充电设置配置。下一步应将典型充电负荷日按照节假日和工作日加以区分,找出2种负荷日之间的差异。一旦建成较为完善的充电网络,将在一定程度上减少用户的充电困难,有利于促进电动汽车的在高寒地区的推广应用。
| [1] |
田立亭, 史双龙, 贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术, 2010, 34(11): 126-130. |
| [2] |
郭晓斌, 张乐平, 赖宇阳. 不同模式下电动汽车充电负荷及充电设施需求数量计算[J]. 电网与清洁能源, 2013, 29(11): 76-81. DOI:10.3969/j.issn.1674-3814.2013.11.017 |
| [3] |
杨冰, 王丽芳, 廖承林, 等. 不确定充电习惯对电动汽车充电负荷需求及充电负荷调节的影响[J]. 电工技术学报, 2015, 30(4): 226-232. DOI:10.3969/j.issn.1000-6753.2015.04.028 |
| [4] |
Leou R C, Teng J H, Su C L. Modelling and verifying the load behaviour of electric vehicle charging stations based on field measurements[J]. Generation Transmission & Distribution Iet, 2015, 9(11): 1112-1119. |
| [5] |
Yagcitekin B, Uzunoglu M, Karakas A, et al. Assess ment of electrically-driven vehicles in terms of emission impacts and energy requirements:a case study for Istanbul, Turkey[J]. Journal of Cleaner Production, 2015(96): 486-492. |
 2018, Vol. 36
2018, Vol. 36