2. 中广核风电有限公司内蒙古分公司, 呼和浩特 010070
2. China Guangdong Nuclear Wind Power Co., Ltd., Inner Mongolia Branch, Hohhot 010070, China
永磁直驱型风力发电机组一般采用的控制策略是按照最优增益系数为定值进行设计的,然而风电场一年四季气温、气压的变化都比较大,在实际运行过程中,最优增益系数是随空气密度变化而变化的,如果最优增益系数仍按照定值进行设置,机组就无法按照最佳叶尖速比进行控制,从而导致机组不能实现最大风能利用效率[1-3]。
本文通过搭建仿真平台,对定值最优增益系数和自适应增益系数两种控制策略进行仿真,为风力发电机组的优化运行提供理论依据。
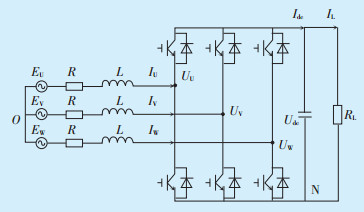
1 直驱型风力发电机数学模型三相直驱型风力发电机主电路拓扑结构如图 1所示。
|
图中:EU、EV、EW—三相并网电压,L—三相滤波电感;R—网侧电阻;RL—直流侧电阻;UU、UV、UW—交流侧电压;IU、IV、IW—交流侧电流;Udc—直流侧电压;Idc—直流侧电流 图 1 三相直驱型风力发电机主电路拓扑结构 |
根据图 1在dq同步旋转坐标系下建立永磁同步发电机组数学模型[4-8],如公式(1)所示。

|
(1) |
式中 Id—有功电流;
Iq—无功电流;
Ud—有功电压;
Uq—无功电压;
Ed、Eq—电压扰动项。
永磁直驱型风力发电机组中发电机由永磁体励磁,在变流控制器和发电机间不存在无功交换,通过SVPWM控制电压矢量Ud、Uq的方式来控制发电机的转速。为实现变流器功率因数为1,需要控制q轴电流参考值Iq*=0,d轴和q轴之间除了受Ud、Uq影响,还存在交叉耦合项ωLIq、-ωLId,对此采用前馈补偿的控制方法进行解耦,引入新变量:
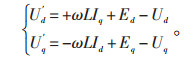
|
(2) |
据此得到转速控制器模型如图 2所示,直驱型风力发电机控制框图如图 3所示。
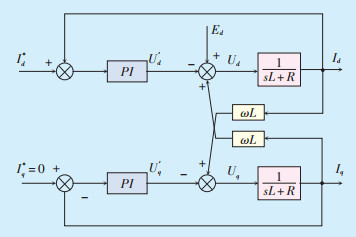
|
图 2 发电机转速控制器模型 |
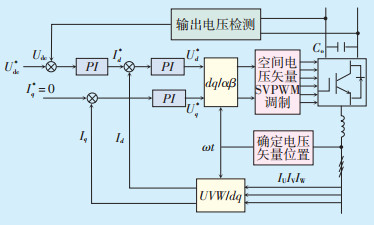
|
图 3 直驱型风力发电机控制框图 |
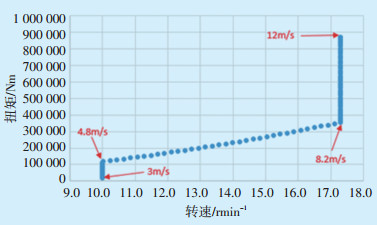
永磁直驱型1.5 MW风力发电机组功率P计算公式见式(3),其转速和扭矩的关系曲线见图 4。图 4中转速在10~17.3 r/min区间的曲线为最大风能利用系数Cp运行区间。扭矩与转速间的关系见公式(4),其中最优增益系数Kopt计算方法见公式(5)。由公式(5)可知最优增益系数Kopt与当地空气密度ρ相关,而空气密度总是随海拔高度和环境温度变化而偏离设计值(1.225 kg/m3),因此最优增益系数也会随环境变化而变化。对此可以在风力发电机上加装用以跟踪空气密度的设备,以得到机组的最优增益系数。空气密度计算公式见公式(6)。
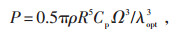
|
(3) |
|
图 4 转速和扭矩的曲线关系 |
式中 Ω—发电机转速,r/min;
R—叶轮扫风面半径,m;
Cp—最大风能利用系数;
λopt—最优叶尖速比。
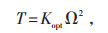
|
(4) |
式中 T—发电机扭矩,Nm。
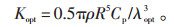
|
(5) |
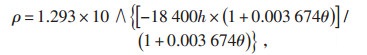
|
(6) |
式中 h—海拔,m;
θ—环境温度,℃。
2.2 建立仿真模型常规控制策略中,最优增益系数Kopt为定值,并不随空气密度的变化而变化,风力发电机的最佳风能利用系数Cp达不到最佳。根据公式(5),最优增益系数Kopt中包含空气密度ρ,而ρ会随着周围环境如温度、海拔等因素变化而变化,此时风力发电机的机械扭矩也会随之变化,若电磁扭矩仍按照公式T=KoptΩ2(Kopt为定值)进行控制,叶尖速比λopt将不能保持最优,风力发电机也无法最大程度地吸收风能。通过改变控制策略,将最优增益系数Kopt设置为随空气密度ρ变化的变化量时,叶尖速比λopt则能维持在最优,此时风力发电机能最大程度地吸收风能。
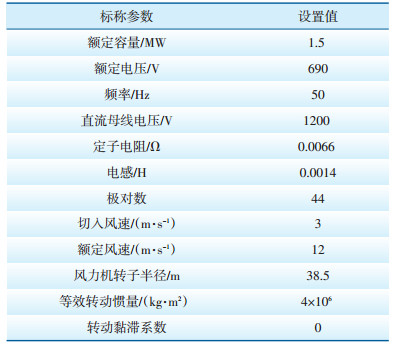
根据图 3,运用Matlab/Simulink仿真软件搭建仿真模型,模拟在空气密度变化的情况下,最优增益系数Kopt分别以定值(基于ρ=1.225 kg/m3)和变化值(随空气密度变化而变化)两种情况加以控制,并对仿真结果进行分析,以验证控制方案的有效性,Matlab/Simulink仿真参数设置如表 1所示。
| 表 1 具体参数设置 |
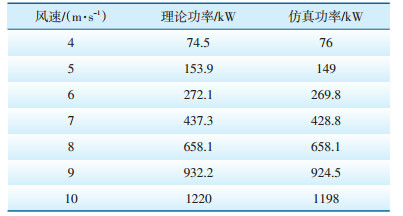
在风速4~10 m/s条件下对风力发电机模型进行仿真,将仿真功率与风机厂家提供的理论功率相比较,结果如表 2所示。由表 2可知仿真功率与理论功率差值在5%以内,验证了仿真模型的准确性。
| 表 2 理论数据与仿真数据对比 |
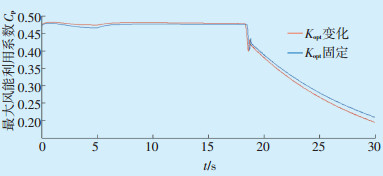
在两种控制方案下,风力发电机从并网到满发过程的仿真结果如图 5所示。在最大功率跟踪阶段(0~18 s),输出功率随风速的增大而不断上升,此时风力发电机保持最佳叶尖速比,追求最大风能利用系数。图 5显示,Kopt变化时其功率输出及风能利用系数均有所增大,最大风能利用系数平均提升约1%。当风机满发时段(18~30 s),风机开始收桨,此时控制系统以追求额定功率为目的,不再追求最大风能利用系数[9-12]。
|
图 5 两种控制方案下最大风能利用系数比较 |
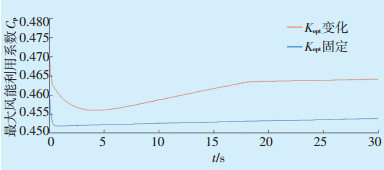
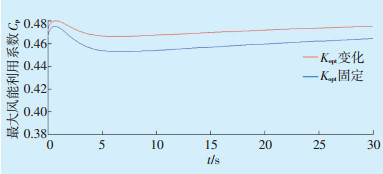
分别以Kopt为定值和Kopt随空气密度变化的变量值进行仿真,选取海拔h=1400 m,环境温度范围-20~20 ℃,仿真结果见图 6—图 8。仿真结果表明,在风速6 m/s、7 m/s、8 m/s 3种工况的稳定阶段,Kopt变化时的风能利用系数Cp明显优于Kopt为定值时的情况,约提升1%,可见控制策略的改变直接影响到最大风能利用系数Cp的输出。
|
图 6 6 m/s风速下两种控制策略最大风能利用系数 |
|
图 7 7 m/s风速下两种控制策略最大风能利用系数 |

|
图 8 8 m/s风速下两种控制策略最大风能利用系数 |
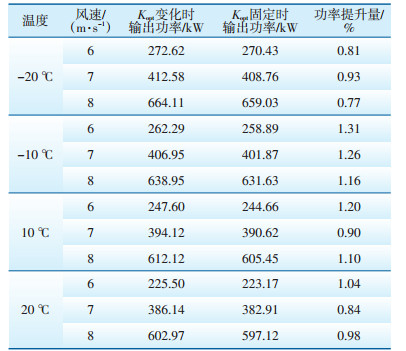
为了进一步定量分析Kopt变化与Kopt固定两种控制策略对应的风力发电机功率输出值,选取-20 ℃、-10 ℃、10 ℃、20 ℃作为全年典型温度进行仿真,以风速6m/s、7 m/s、8 m/s为全年典型风速,两种控制策略下的仿真数据对比见表 3。由表 3可知,在不同的温度和风速条件下,Kopt变化时的功率输出明显优于Kopt为定值时的功率输出,约提升1%。
| 表 3 两种控制方案下的仿真数据对比 |
通过对定值最优增益系数和随空气密度自适应最优增益系数两种策略的仿真,明确了最大风能利用系数和风机输出功率受环境空气密度的影响关系。仿真结果表明,空气密度自适应最优增益系数的控制策略下最大风能利用系数和风机的输出功率均有所提升。
| [1] | 徐锋, 王辉, 杨韬仪. 兆瓦级永磁直驱风力发电机组变流技术[J]. 电力自动化设备, 2007, 27(7): 57–61. |
| [2] | 文贤馗, 肖永, 林呈辉, 等. 贵州高原山区空气密度对风电功率影响研究[J]. 中国电力, 2014, 47(7): 101–103. |
| [3] | 刘丽丽. 风电场空气密度对风电机组发电量影响的研究[J]. 风能, 2015(12): 86–88. DOI:10.3969/j.issn.1674-9219.2015.12.034 |
| [4] | 孙攀, 陶保震, 袁博. 永磁直驱风电机组并网系统的建模与仿真研究[J]. 风能, 2014(12): 98–101. DOI:10.3969/j.issn.1674-9219.2014.12.029 |
| [5] | 张文秀, 武新芳, 孙娟. 基于反馈线性化的直驱风力发电机组控制系统[J]. 电机与控制应用, 2014(8): 46–50. |
| [6] | 童克诚, 孙赟. 基于直接反馈线性化的永磁直驱风力发电系统[J]. 广东电力, 2016, 29(2): 21–24. |
| [7] | 王武. 永磁同步风电系统建模及直接反馈线性化控制[J]. 机电工程技术, 2015(5): 39–43. |
| [8] | 张梅, 何国庆, 赵海翔. 直驱式永磁同步风力发电机组的建模与仿真[J]. 中国电力, 2008, 41(6): 79–84. |
| [9] | 肖园园, 李欣然, 张元胜, 等. 直驱永磁同步风力发电机的等效建模[J]. 电力系统及其自动化学报, 2013, 25(1): 12–17. |
| [10] | 刘向向, 李新宇, 王奔. 变结构控制策略在直驱永磁同步风力发电机中的应用[J]. 电网技术, 2013, 37(2): 520–525. |
| [11] | 杨超, 王志, 叶小广. 基于SCADA数据的风电机组技术改造后评估方法研究[J]. 华电技术, 2017, 39(1): 21–23. |
| [12] | 郭丹, 朴在林, 胡博, 等. 风电场运行数据分析[J]. 电网与清洁能源, 2016, 32(4): 93–98. |
 2018, Vol. 36
2018, Vol. 36