汽轮发电机组振动问题是影响机组安全稳定及经济运行的重要因素,现场振动故障统计分析表明,引起机组振动大的激振力绝大多数为转子不平衡力[1]。一般情况下,动平衡是治理该类振动故障既经济又有效的措施,因而在机组振动问题现场处理中得到广泛应用。
制订动平衡方案时,经常需要综合考虑相邻多测点、多工况[2](如临界转速、工作转速、带负荷等)下的机组振动情况。当不同工况、不同测点振动配重矢量出现矛盾时,可以采用矢量优化法进行寻优解决。
1 矢量优化法介绍 1.1 矢量优化法原理及编程应用方法矢量优化法的基本思路是根据机组振动参数对试加质量的响应,通过“试凑”方法求出最优平衡方案。该方法的关键点在于“试凑”的算法[2],本文采用Delphi软件进行编程,算法如下:
(1)进行试加重,应用影响系数法求出不同测点、不同工况对应的配重矢量P1~Pk。
(2)求出配重矢量中的质量最大值mmax和质量最小值mmin,按一定步长展开形成质量数列M;将角度按一定步长(如5°)展开,形成角度数列N,通过组合得到m×n个配重矢量。
(3)分别将这m×n个配重矢量代入之前试加重得到的影响系数,求取相应测点的残余振动值;当各残余振动值都较小时(此环节可采用最小二乘法求解),该平衡矢量即为最优解。
1.2 矢量优化法的特点基于其理论假设,矢量优化法具有如下优点:
(1)兼顾了临界转速和工作转速下的振动问题;
(2)同时顾及空负荷和满负荷下的振动情况;
(3)综合考虑了多测点的振动值。
可以看到,矢量优化法也是1种基于影响系数法的数学寻优方法,同样因不涉及力学本质,使用时存在以下潜在风险:与影响系数法一样,同样存在累积误差;多矢量寻优算法的精确性对计算结果的满意度有较大影响。
1.3 矢量优化法常用场合经验表明,在转子支承正常的情况下,转子跨内配重通常会对转子两端振动值产生同趋势的影响。但对于三支承结构,因现场条件限制需在跨外联轴器配重时,配重矢量对联轴器两端轴承及转子另一端轴承的影响容易出现矛盾情况,此时即可用矢量优化法来寻优;当转子另一端轴承较为敏感时,通常也需要应用矢量优化法来处理。
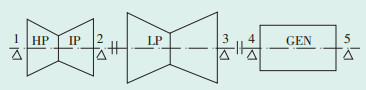
2 矢量优化法应用实例 2.1 设备概况某电厂2号汽轮发电机组为武汉汽轮电机股份有限公司生产的C125/N150-13.24/0.245/535/535型超高压、一次中间再热、单轴双缸双排汽、单抽汽凝汽式汽轮机。机组轴系由汽轮机高中压转子、低压转子和发电机转子组成,轴系结构和支撑状况如图 1所示,表 1为机组轴系的设计临界转速。
|
图 1 机组轴系结构与支撑状况示意图 |
| 表 1 机组轴系设计临界转速 |
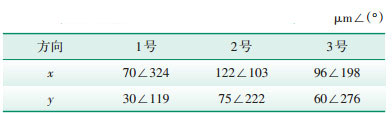
该机组长期运行后,2号轴承出现了轴振较大的问题,配重前76 MW负荷工况下1号—3号轴承基频轴振数据如表 2所示。
| 表 2 配重前1号—3号轴承轴振数据 |
(1)从临界转速区域1号—3号轴承轴振情况看,高中压转子一阶不平衡质量很小,低压转子一阶不平衡质量也较小。
(2)工作转速下1号—3号轴承轴振表现为较为稳定的基频强迫振动,基频幅值及相位均较稳定,分析认为2号轴承附近存在一定的不平衡质量。考虑到1号、2号轴承轴振中反相分量较大,认为高中压转子可能存在二阶不平衡质量,低压转子也可能存在一定的不平衡量。
(3)另外,因3号轴承轴振值在低速(500 r/min)下仍维持在100 μm以上,反映出附近轴颈存在晃度大问题[3]。
因受现场条件限制,高中压转子和低压转子上不易进行配重操作,因此决定在2号轴承附近的联轴器上进行动平衡配重。
2.3 首次配重后振动情况结合机组轴系结构、支承特点及高中压转子、低压转子的临界转速数据,二阶配重选取较小的滞后角[4],经权衡后实际在中低压转子联轴器处合计配重0.7 kg∠258°。
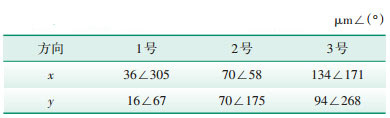
首次配重后机组再次启动,机组转速3000 r/min时1号—3号轴承的轴振数据(基频)如表 3所示。
| 表 3 首次配重后1号—3号轴承轴振数据 |
对比表 2、表 3数据,可以看出首次配重后1号、2号轴承轴振显著下降,而3号轴承的轴振值反而有所增加。
通过2次配重计算,认为1号轴承的最佳消振配重位置在239°,2号轴承的最佳消振配重位置在223°,而3号轴承的最佳消振配重位置则在147°。因后者与前两者的偏差较大,故采用矢量优化法寻优解决。
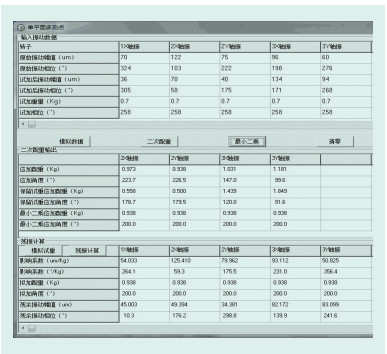
2.4 矢量优化法寻优按照矢量优化法(计算页面截图如图 2所示)求得应加矢量为0.938 kg∠200°,配重后预计各轴承残余振动值见图 2。
|
图 2 矢量优化法算例截图 |
受联轴器承载能力、安装位置限制,取消原配重矢量0.7 kg∠258°后,第2次实际施加的配重矢量为0.79 kg∠190°。
第2次配重完成后,机组再次启动,转速在3000 r/min时1号—3号轴承的轴振数据见表 4。从表 4可以看出,机组各轴承的轴振通频值均小于90 μm,处于国家标准规定的A区域(振动值优良区域)[5],实际残余振动与预计残余振动的偏差在可接受范围内,机组可以长期安全稳定运行,应用矢量优化法进行了2次配重后取得了较好的消振效果。
| 表 4 第2次配重后1号—3号轴承的轴振数据 |
机组振动处理时的现场动平衡工作需追求在最少启动次数下取得最佳的消振效果[6-8],以实现机组运行安全性与经济性的统一。为达到这一目标,当不同工况、不同测点的平衡方案发生矛盾时,矢量优化法可以提供较好的解决策略。从实用角度出发,现场应用该方法时,应尽可能选取原始振动大、应加矢量矛盾大而数量较少的测点参与计算,有助于提高寻优结果的满意度。应用矢量优化法处理机组振动的案例取得了良好的消振效果,可供其他电厂在处理机组类似振动问题时参考。
| [1] | 张学延. 汽轮发电机组振动诊断[M]. 北京: 中国电力出版社, 2008. |
| [2] | 杨建刚. 旋转机械振动分析与工程应用[M]. 北京: 中国电力出版社, 2007. |
| [3] | 李晓波, 张沈彬, 江建勋. 350 MW新机启动振动故障诊断与处理[J]. 内蒙古电力技术, 2012, 30(5): 108–110. |
| [4] | 施维新. 轴系平衡一次加准法的研究及应用[J]. 中国电力, 2005, 38(3): 47–53. |
| [5] | 全国机械振动与冲击标准化技术委员会. 旋转机械转轴径向振动的测量和评定: GB/T 11348. 2-1999[S]. 北京: 中国标准出版社, 1999. |
| [6] | 寇胜利. 汽轮发电机组的振动及现场平衡[M]. 北京: 中国电力出版社, 2007. |
| [7] | 陈武. 基于多类数据及模型融合的设备评价分析研究[J]. 电力大数据, 2017, 20(9): 14–16. |
| [8] | 王可. 600 MW机组冷态启动振动大原因分析和处理[J]. 电力大数据, 2017, 20(9): 71–73. |
 2017, Vol. 35
2017, Vol. 35