2. 神华内蒙古国华准格尔发电有限责任公司, 内蒙古 鄂尔多斯 010300
2. Inner Mongolia Guohua Zhungeer Power Generation Co., Ltd., Ordos 010300, China
由于国家环保要求日益严格,火电厂普遍采用低氮燃烧、高效率SCR(选择性催化还原法)脱硝装置等技术对锅炉进行改造,使其排放的NOx质量浓度显著下降。大量试验表明,煤质差异不大时,不同的运行方式会造成锅炉省煤器出口NOx质量浓度(以下简称NOx质量浓度)差异明显,同时也会影响锅炉热效率,因此对锅炉进行低氮燃烧优化意义重大。然而,炉内煤粉燃烧是1个多因素耦合、复杂且非线性的物理和化学反应过程,燃烧数据分析非常困难。目前主要采用的研究方法有锅炉燃烧调整研究、锅炉燃烧数值模拟研究、锅炉燃烧智能算法建模研究。前2种方法受试验条件、人员素质、模型精度等因素影响,因此,基于现场试验数据和人工智能算法进行数学建模,开展NOx质量浓度及锅炉燃烧效率模拟计算研究具有重要意义[1]。
本文以某发电公司330 MW机组锅炉为研究对象,利用人工神经网络的联想、记忆、自适应和容错功能对锅炉效率和NOx质量浓度进行仿真建模,利用遗传优化算法对锅炉燃烧过程进行优化仿真,以获取兼顾锅炉效率和NOx质量浓度的运行策略。
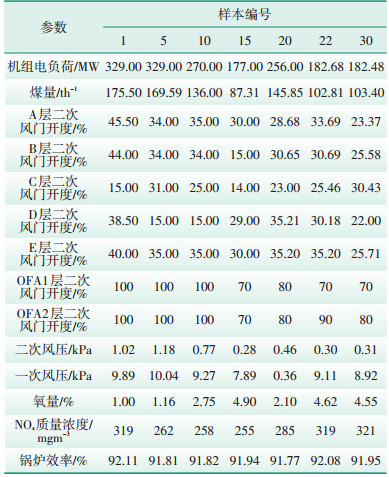
1 低氮燃烧改造后的优化试验某发电公司330 MW机组锅炉系北京巴布科克·威尔科克斯有限公司设计生产的亚临界参数、一次中间再热、前后墙对冲燃烧、分隔式大风箱、固态排渣燃煤汽包炉,2013年采用低氮燃烧器技术、空气分级燃烧技术进行了低氮燃烧改造。A、B、C层燃烧器更换为Airjet型低氮燃烧器,D、E层燃烧器更换为DRB-4Z型低氮燃烧器。针对更换后的燃烧器现场着火特性与锅炉本体参数变化,采用了变燃烧器旋流强度、变内外配风比和变OFA旋流强度等燃烧调整措施。结合单因素试验与正交试验原则,在多个负荷工况下,进行了变氧量、变风煤比、变OFA风门开度、变二次风配风方式的燃烧优化试验,以获得兼顾NOx质量浓度和锅炉效率的最优结果。经筛选获取30组典型代表工况参数,作为BP神经网络建模数据(部分数据见表 1)。
| 表 1 低氮燃烧改造后优化试验数据 |
BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,由输入层、隐层、输出层构成,该模型被称为“黑箱”模型,即不需要知道输入量对输出量的影响关系即可构建两者之间的非线性映射,具有预测精度高和泛化能力强、应用广泛的特点[2-3]。
2.1 输入、输出参数设定依据燃烧原理与现场燃烧优化试验,分析影响锅炉效率与NOx质量浓度的可控必要因素:煤质差异直接影响锅炉效率,煤质基础数据包括元素分析及发热量,考虑到现场无法开展入炉煤元素分析,因此将入炉煤量、机组负荷作为输入要因;氧量、二次风门及OFA风门控制是低氮燃烧技术与分级燃烧技术的关键,因此将一次风压、二次风压、省煤器出口氧量、二次风风门及OFA风风门开度作为输入要因,输入要因共计12个。网络输出参数选取NOx质量浓度与锅炉效率。为了确保网络不会因为数据分散且数量级差异悬殊而导致不收敛,且正确反映输入变量对输出变量的影响,需要对输入、输出数据进行标准化归一处理,将输入、输出变量均归一化到[-1, 1]区间。
2.2 网络设计与优化 2.2.1 网络设计依据优化试验数据分析锅炉可控运行参数与燃烧特性之间的关系,选用3层BP神经网络构建燃烧过程仿真模型。输入层作为样本输入参数接受缓冲,其神经元激活函数选取S型logsig对数传输函数,神经元数目为输入参数个数,共12个;隐层是BP网络的核心,实现输入参数到输出参数的非线性映射,其神经元激活函数也选取S型logsig对数传输函数,神经元数目结合经验公式与模型测试情况定为25个;输出层神经元激活函数选取purelin线性传输函数,神经元数目为输出参数个数,共2个;BP神经网络训练函数选用反向传播算法trainlm函数,偏差学习函数选用附加动量因子的梯度下降权值学习算法learngdm函数,性能评价函数选用均方误差性能算法mse函数;根据网络仿真需求,网络收敛误差选为1×10-8。
2.2.2 网络权值与阈值优化BP神经网络结构、初始连接权值和阈值的选择直接影响网络学习收敛速度、全局收敛性和网络仿真精度,本文采用遗传算法对BP神经网络进行优化,种群选择50、遗传代数选择100,通过对网络权值与阈值进行编码、解码、种群初始化及适应度计算,实现遗传算法寻优,进而得到更好的网络初始值和阈值。
2.3 网络训练与仿真 2.3.1 网络仿真精度将30组典型数据中的27组数据作为训练样本,其余3组作为测试样本(样本编号为1、10、22,分别代表高、中、低3个负荷工况),训练后的网络可以较准确地对实际物理工况进行仿真预测。仿真结果见图 1、图 2,仿真相对误差见图 3、图 4。相对误差定义为(仿真值—实测值)/实测值×100%。锅炉效率仿真试验中,训练样本的最大绝对偏差为0.04%、最大相对误差为0.05%;测试样本的最大绝对偏差为0.21%、最大相对误差为0.23%。NOx质量浓度仿真试验中,训练样本的最大绝对偏差为3.01 mg/m3、最大相对误差为1.21%;测试样本的最大绝对偏差为11.01 mg/m3、最大相对误差为3.73%。锅炉效率与NOx质量浓度最大误差在工程应用范围内可接受。

|
图 1 锅炉效率仿真曲线 |

|
图 2 NOx质量浓度仿真曲线 |

|
图 3 锅炉效率相对误差仿真曲线 |

|
图 4 NOx质量浓度相对误差仿真曲线 |
神经网络是否优良不仅体现在其对已有数据的拟合能力上,而且体现在对新数据的预测能力(即泛化能力)上。网络的泛化能力与训练能力往往存在一定矛盾:训练能力差时,预测能力也差,随着训练能力的提高,预测能力也提高,但接近极限时,随着训练能力的提高,预测能力反而下降,即出现“过拟合”现象[4]。
依据低氮燃烧技术原理及现场调整试验规律,在众多的可控运行参数中,OFA风门开度与燃烧氧量对NOx生成的影响最为明显。测试样本1的参数是氧量优化试验过程中的1个工况,在其他参数不变的情况下,通过降低送风机入口动叶开度来控制二次风压,将二次风压由1.25 kPa降至1.02 kPa,运行氧量由1.51%降至1.01%,实测NOx质量浓度由345 mg/m3降至319 mg/m3,锅炉效率由92.37%降至92.11%。按照测试样本1的仿真结果,NOx质量浓度仿真值为330 mg/m3,锅炉效率仿真值为92.02%。同样,测试样本10与22的参数均是OFA风门开度优化试验中的工况,3个测试样本的仿真结果已经验证了经过遗传算法优化的BP神经网络泛化能力较强和精确度较高。
3 遗传算法燃烧优化遗传算法是基于生物进化过程中优胜劣汰机制和种群内部染色体信息交换规则,是处理复杂优化问题通用性很强的一类方法,基本操作包括建立适应度函数、编码、选择、交叉和突变。本文基于BP神经网络燃烧仿真模型,应用遗传算法实时调整和计算最优可控运行参数,使锅炉效率和NOx质量浓度达到最佳。
3.1 适应度函数的选取遗传算法在进化搜索中基本不利用外部信息,仅以适应度函数为依据,利用种群每个个体的适应度来进行搜索。因此,适应度函数是遗传算法进行寻优计算的关键,直接影响遗传算法的收敛速度以及能否找到最优解。
根据当前采用的低氮燃烧技术机理分析,通常锅炉效率与NOx质量浓度指标存在一定的互斥性,良好的低氮燃烧效果都会在一定程度上以牺牲锅炉效率为代价。兼顾锅炉效率和NOx质量浓度的锅炉燃烧整体优化就是在保证锅炉安全运行和基本出力的条件下,通过优化运行可控参数,使锅炉效率和NOx质量浓度整体最优。为此定义适应度目标函数如下:

|
式中ρNOx—NOx质量浓度,mg/m3;
η—锅炉效率,%;
a、b—权重,根据对ρNOx与η的关注度取值;
K—常数。
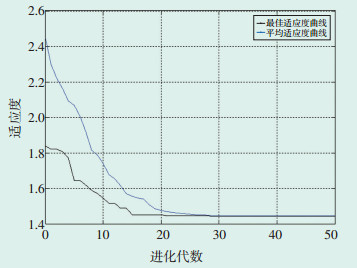
3.2 燃烧优化分析选取机组330 MW工况下,应用基于BP神经网络燃烧仿真模型的遗传算法进行燃烧优化计算,种群数选择50,交叉概率选择0.8,变异概率选择0.2,目标函数权重a、b分别选择0.4、0.6,终止进化代数选择50。由图 5适应度函数曲线可知,平均适应度曲线与最佳适应度曲线变化趋势相同,进化到第30代时,2种曲线基本重合,达到最佳优化值。
|
图 5 适应度函数曲线 |
具体优化比对结果如表 2,优化前配风方式采用均等配风,A、B、D、E投运燃料层二次风风门开度为65%左右、OFA风风门开度为80%、氧量约为3.1%,优化策略将Airjet型燃烧器层对应二次风风门开度开至25%、DRB-4Z型燃烧器层对应二次风风门开度开至36%、OFA风风门全开,氧量控制到1.13%。优化后实测NOx质量浓度由348 mg/m3降至289 mg/m3,锅炉效率由92.37%降至92.02%。优化策略基本符合燃烧优化最优训练工况,煤质偏差不大时,二次风压和配风方式也基本对应相应的运行氧量。
| 表 2 低氮燃烧优化试验数据对比 |
(1)本文基于锅炉低氮燃烧优化试验数据构建的BP神经网络燃烧模型可以准确映射锅炉可控运行参数与锅炉效率和NOx质量浓度之间的非线性关系[5]。
(2)BP神经网络结构、初始连接权值和阈值的选择对网络训练影响很大,直接影响网络学习收敛速度、全局收敛性和网络仿真精度,采用遗传算法对BP神经网络进行优化,可以得到更好的网络初始值和阈值,进而得到泛化能力强、预测精准的网络模型[6-7]。
(3)基于BP神经网络燃烧仿真模型,选择合适的适应度函数,将锅炉效率与NOx质量浓度两个优化指标折算为1个综合指标,利用遗传算法进行燃烧优化计算,最终获取兼顾锅炉效率与NOx质量浓度的运行优化策略,可为现场运行优化提供指导[8]。
| [1] | 吕玉坤, 彭鑫, 赵锴. 电站锅炉热效率与NOx排放混合建模与优化[J]. 中国电机工程学报, 2011, 31(26): 16–22. |
| [2] | 周昊, 茅建波, 池作和, 等. 燃煤锅炉低氮氧化物燃烧特性的神经网络预报[J]. 环境科学, 2002, 23(2): 18–22. |
| [3] | 许昌, 吕剑虹. 基于生成机理的燃煤电站锅炉NOx排放量神经网络模型[J]. 中国电机工程学报, 2004, 24(10): 233–237. DOI:10.3321/j.issn:0258-8013.2004.10.046 |
| [4] | 陆军, 张广才, 徐党旗, 等. 改进BP神经网络在低氮燃烧优化中的应用[J]. 热力发电, 2015, 44(4): 106–110. |
| [5] | 曹庆才, 高德欣, 刘芳, 等. 基于神经网络与遗传算法的锅炉燃烧优化系统设计[J]. 工业控制与应用, 2016, 35(6): 10–14. |
| [6] | 周昊, 朱洪波, 岑可法. 基于人工神经网络和遗传算法的火电厂锅炉实时燃烧优化系统[J]. 动力工程, 2003, 23(5): 2665–2669. |
| [7] | 张耀. 低氮燃烧改造在电厂应用研究[J]. 贵州电力技术, 2014, 17(1): 24–27. |
| [8] | 韩义, 李鑫, 刘永江, 等. 330 MW机组锅炉低氮燃烧技术改造[J]. 内蒙古电力技术, 2016, 34(5): 63–66, 79. |
 2017, Vol. 35
2017, Vol. 35