2. 内蒙古工业大学电力学院, 呼和浩特 010080;
3. 内蒙古电力科学研究院, 呼和浩特 010020;
4. 内蒙古电力经济技术研究院, 呼和浩特 010020
2. Inner Mongolia University of Technology, Hohhot 010080, China;
3. Inner Mongolia Electric Power Research Institute, Hohhot 010020, China;
4. Inner Mongolia Electric Power Economic and Technological Research Institute, Hohhot 010020, China
随着电力市场化改革,开放的交易市场正在逐步形成,为实现输电资源利用最大化,系统内会存在多个输电交易,电网充当输电角色。电能在传输过程中会产生损耗,如何合理分摊损耗是目前要解决的主要问题。
常用网损分摊方法有邮票法、潮流跟踪法、逐线计算法等[1]。不同网损分摊方法对分摊结果的影响可达4%~10%[2]。邮票法以交易量占总供电量的比例分摊网损,计算简单,但未考虑实际负荷位置和交易距离;潮流跟踪法基于潮流计算,但仅考虑潮流对网损的影响,对交易之间相互作用没有做相关分析,计算结果对用户不公平;逐线计算法结合了线路长度和潮流等因素,但忽略了用户加入系统交易的先后次序,分摊结果未考虑网损的交叉项问题。
博弈论是现代数学的一个分支,是专门研究2个或2个以上利益有冲突的个体[3]。如何使输电资源利用合理化、经济化,且分摊方案合理是博弈问题。Shapley值分摊法是解决博弈问题的一个方法,大量实验数据表明,Shapley值分摊方法稳定性好,最终结果唯一,可以向系统内成员提供经济鼓励信号[4]。但Shapley值分摊方法仅适用于少交易系统[5],针对实际网络,由于交易数目过多,出现交易组合“爆炸”而无法计算。本文基于双边Shapley值分摊法来解决交易组合“爆炸”问题[6],该方法在调峰补偿、阻塞分摊以及互联网方面都有应用,双边Shap-ley值分摊法同样适用于电网网损分摊。
1 Shapley值分摊法简介 1.1 数学模型设电网中有n个交易,即n个联盟成员,S为交易组合联盟,则采用Shapley值分摊法进行网损分摊的数学模型为:
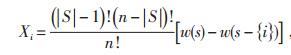
|
(1) |
式中Xi—交易参加联盟分摊的网损值,其中i为参与系统内网损分摊的某个交易;
S—含有交易i的联盟;
|S| —联盟中所有交易个数;
n—参加网损分摊交易总个数;
w(s)—求网损的表达式,当系统内没有交易时,w(0)=0;
w(s-{i})—在系统联盟中除去交易i的损耗;[w(s)-w(s-{i})]—交易i参与联盟S时,给联盟造成的网损增加值,即联盟S边际网损;
n!—全部交易可能加入联盟先后次序的阶乘。
1.2 优点与其他分摊方法相比,Shapley值分摊法和结果可保证收支平衡、解决交叉项分摊问题、确保分摊结果公平,基于Shapley值分摊法把系统总网损分摊给各个用户的方法是合理的,市场参与方容易接受分摊结果,具有很好的经济意义[7]。
1.3 存在的问题假如输电网中存在n个交易,使用Shapley值分摊法进行网损分摊,计算联盟组合个数为2n-1,当交易个数n变大,计算量便会以指数级增加,不利于实际工程计算。对此采用改进Shapley值分摊法,即双边Shapley值分摊法,以解决Shapley值分摊法在多交易网损分摊中遇到的难题。
2 双边Shapley值分摊法当系统里存在多交易参与博弈时,由于系统交易过多导致交易组合出现“爆炸”,为方便工程计算,Ketchpel提出双边Shapley(Bilateral Shapley Value)值思想,简称BSV值分摊方法[8],解决局中人完全离散的双边交易问题。基于双边Shapley值形成的交易联盟,同样适用于电力传输问题[9]。
2.1 数学模型设S∈W(N)为多个局中人,N={1,2,3,…,n}为联盟子集,其中:
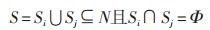
|
(2) |
由式(2)可知S为Si和Sj不相交的双边联盟,则联盟S中Si按双边Shapley值分摊法定义为:
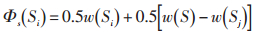
|
(3) |
Si和Sj为S的基础联盟,w(S)是联盟S特征函数。由式(3)可知,Φ(Si)由两部分构成,一是获得自身的一半,即0.5w(Si);二是获得该联盟对整个联盟S贡献的一半,即0.5[w(S)-w(Sj)]。由此可知,基础联盟对总联盟S的贡献体现了各局中人在联盟里的作用。
2.2 网损计算方法假设系统中存在3个交易,即n=3,则局中人集合为I={1,2,3},共形成7个交易组合联盟:{1}、{2}、{3}、{1,2}、{1,3}、{2,3}、{1,2,3}。采用双边Shapley值计算网损分摊值时从总联盟S{1,2,3}出发,把总联盟分为2个基础联盟S{2,3}和S{1}共同承担网损,即:
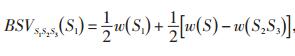
|
(4) |
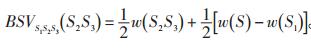
|
(5) |
其中,式(4)为交易1承担的网损,式(5)为交易2和3共同作用时的网损。
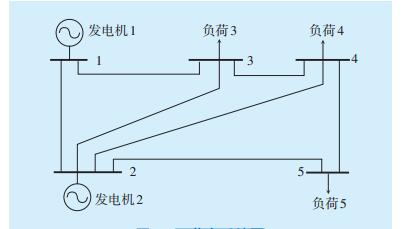
3 算例分析 3.1 五节点电力系统图 1为五节点电力系统图,由2台发电机和3个负荷组成,五节点系统线路参数见表 1,五节点系统交易网损数据见表 2,其中发电机1有功功率为67.5MW,发电机2有功功率为150MW。经计算每个交易组合下产生的网损见表 3,每个交易分别基于不同方法分摊网损值见表 4。
|
图 1 五节点系统图 |
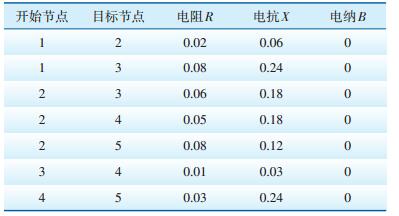
| 表 1 五节点系统线路参数(标幺值) |
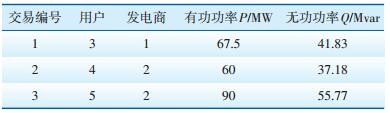
| 表 2 五节点系统交易数据 |
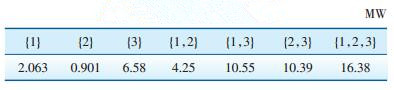
| 表 3 五节点系统交易网损 |
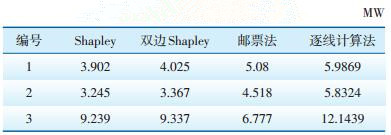
| 表 4 不同分摊方法网损分摊值 |
由表 4中数据可知,邮票法基于比例分摊,尽管考虑交叉损耗,但并未明确归属,因此网损分摊结果误差较大;逐线计算法过分夸大后加入者作用,将交叉损耗全部归属后加入者,网损分摊过大,对用户不公平;Shapley值和双边Shapley值分摊方法均考虑交叉项损耗,基于一定权值分摊给交易,这两种方法计算结果接近。因此,双边Shapley值分摊结果相比Shapley值分摊结果尽管存在一定误差,但比其他两种分摊结果要精确得多,工程上可以作为Shapley值分摊法的近似解。
3.2 自备电厂转供算例蒙西电网A企业自备电厂通过公用电网的输电线路为所属企业负荷提供电能,但该企业以自备电厂上网量和负荷用网量的差值与电力公司进行电费核算,忽略了电能在传输过程中造成的损耗,电网利益受到一定威胁。因此,当前解决的主要问题是确定自备电厂因转供该承担的损耗。
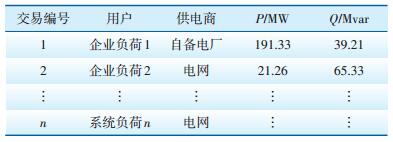
基于蒙西电网2015年8月代表日数据进行定量仿真计算。由于该地区电网复杂,为结合双边Shapley值分摊法求解,可以假设系统内存在n个交易,即每个负荷电能可能由1个或多个发电厂供电,该自备电厂转供就属于n个交易中的1个交易,根据双边Shapley值分摊法便可以计算出该自备电厂转供分摊的网损。系统1时刻交易数据如表 5,由表中数据可知该企业用电量由电网和其自备电厂共同提供。为求取自备电厂转供电量,可以把企业负荷分为2部分,其中企业负荷1即为自备电厂转供电量,企业负荷2为该企业部分电量由电网供电。
| 表 5 系统1时刻交易数据 |
基于RTLAS潮流程序计算得到以下结果:
(1)交易1单独运行时网损为:w(1)=2.0609MW;
(2)其他交易(除交易1)同时进行时网损为:w(2,3,…,n)=173.5324MW;
(3)所有交易同时进行时网损为:w(1,2,3,…,n)=174.5814MW,小于w(1)+w(2,3,…,n),由此可知交叉项损耗为负值。
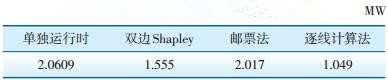
基于以上数据采用双边Shapley值分摊法、邮票法和逐线计算法分别计算自备电厂因转供(交易1)承担的网损,结果如表 6所示。
| 表 6 交易1不同分摊方法网损分摊值 |
由表 6中数据可知双边Shapley值分摊结果(1.555MW)相比交易1单独运行时(2.0609MW)要小,原因为本文所研究自备电厂和负荷都位于电网富电力区,电力输送造成的损耗较小。采用邮票法分摊结果误差较大;双边Shapley值法基于一定权值将交叉项损耗进行分摊,而本算例中由于交叉项损耗为负值,其分摊值会大于采用逐线计算法计算的分摊结果,与表 6中计算结果相一致。
4 结论采用Shapley值分摊法,需要考虑系统内22-1个交易联盟网损值,常因计算量大而无法计算;而针对双边Shapley值法计算各交易分摊网损时,只需对2n+1个交易联盟进行网损值计算即可,大大简化了计算过程。当实际电力系统随交易n逐渐增大,双边Shapley值法简化计算优点更加明显,其计算结果比其他方法要精确得多,且计算结果和采用Shapley值分摊法计算结果相近。在进行输配电价核算时,为简化计算允许存在一定的误差,因此作为Shapley值分摊法的一种改进方法,双边Shapley值分摊法在实际工程计算中可以代替Shapley值分摊法进行求解。
| [1] | 谭艳妮. 网损分摊方法研究[D]. 北京: 华北电力大学, 2015. |
| [2] | 孙华东, 汤涌, 马世英. 电力系统稳定的定义与分类述评[J]. 电网技术, 2006, 30(17): 31–35. DOI:10.3321/j.issn:1000-3673.2006.17.006 |
| [3] | 丁婕斐. 基于博弈论的智能电网PHEV电能调度算法研究[D]. 广州: 广东工业大学, 2015. |
| [4] | 高晓晶. 基于改进Shapley值的输电费用分摊方法研究[D]. 武汉: 湖北工业大学, 2013. |
| [5] | 胡朝阳, 韩祯祥. 基于Shapley值的网损分摊新方法[J]. 电力系统自动化, 2003(7): 32–35. |
| [6] | 谢俊, 张晓花, 吴复霞, 等. 基于合作博弈论和工程方法的调峰费用分摊[J]. 电力系统保护与控制, 2012(11): 16–23. DOI:10.3969/j.issn.1674-3415.2012.11.004 |
| [7] | 陈锐. 基于Shapley值的双边交易阻塞分摊方法[D]. 长沙: 湖南大学, 2005. |
| [8] | Javier Contreras. Coalition Formation in Transmission Expansion Planning[J]. IEEE Transaction on power systems, 1999, 14(3): 1144–1152. DOI:10.1109/59.780946 |
| [9] | Jerome Yen, Yonghe Yan, Javier Contreras. Multi-agent Approach to the Planning of Power Transmission Expan sion[J]. ExpanDecision Support Systems, 2000, 11(28): 279–290. |
 2017, Vol. 35
2017, Vol. 35