2. 华北电力大学能源与动力工程学院, 北京 102206
2. North China Electric Power University, Beijing 102206, China
并入电网的发电厂,由于系统负荷变化,主要热力设备经常在变工况下运行,对此需寻求1套最佳运行方案,以获得最大的经济性,即将电网需要的负荷在各台机组间合理分配,以获得最佳经济效益,达到机组间负荷最优分配[1-5]。
对于电厂的电力负荷调度,较合理的方式是以1个电厂或竞价上网的实体作为1个调度单元,机组间的负荷分配由调度单元自己内部解决,或者由调度单元根据其竞价得到某一时段的上网电量,提供单元内机组在这一时段内的负荷曲线,调度中心根据该曲线进行负荷调度,以最大限度保证电网内各机组的工作效率,降低发电成本。本文针对等微增和动态规划算法对电力调度结果进行分析,以找到更合理的机组负荷调度优化方式。
1 等微增算法和动态规划算法的数学模型 1.1 等微增算法[6-9]等微增算法是以数学极值理论为基础,将各机组煤耗微增率相等的负荷点,确定为负荷分配的最优方案。火电机组的耗量特性是指机组在稳定状态运行时的燃料量和功率之间的关系。假设有n台机组,其耗量特性曲线可用二次型表示,即:

|
(1) |
式中Bj第j台机组的煤耗量,t/h;
Pj第j台机组的负荷,MW,j=1,2,…,n;
a0、a1、a2—耗量特性方程系数。
由拉格朗日(Lagrange)乘数法构造一个辅助函数B*,设λ为拉格朗日乘子,对于每个总负荷

|
(2) |
式中Pi以i为角标表示的功率,MW,i=1,2,…,n。
对式(1)求导,并将(2)代入(1)可以得到等微增算法数学模型:

|
(3) |
动态规划(Dynamic Programming)是运筹学的一个分支,是求解多阶段决策问题的最优化方法。一个多阶段决策过程最优化问题的动态规划模型通常包含阶段、状态、决策和策略4个要素。
选取机组台号i为决策阶段,机组负荷Pi为决策变量,将累计的机组成本选为状态变量。用状态变量si表示分配给第i台机组至第n台机组的负荷,决策变量ui表示分配给第i台机组的负荷,即ui=Pi。状态转移方程:

|
(4) |
允许决策集合:

|
(5) |
令最优值函数fi(si)表示以状态变量为si的负荷分配给第i台机组至第n台机组所得的最小煤耗量,则可以写出动态规划的逆推关系式为:

|
(6) |
利用公式(6)进行逐段计算,最后求得f1(P0)即为采取动态规划算法得到的机组成本最低的最优负荷分配。
2 机组煤耗量的获取[10] 2.1 煤耗量获取方法要进行机组间的负荷分配需首先得到机组的耗量特性。发电企业获取机组耗量特性一般采用以下2种方式:一是根据机组较长时间的运行记录和试验运行数据,得出机组的耗量特性;二是将制造厂商的设计数据与长期运行的数据相结合,得出机组的耗量特性。
进行理论研究时还有一种反平衡变工况算法计算煤耗量。本文所用煤耗量源于反平衡算法所得煤耗与电厂运行记录煤耗的综合比较。
2.2 反平衡计算煤耗量以1台300 MW机组进行负荷分配为例,对反平衡算法计算煤耗量进行说明。计算时需了解机组在不同负荷下的煤耗情况,因此需进行热力系统的变工况计算。如果该机组的允许负荷变动在70%~ 110%,以5 MW为1个间隔,则需分别计算该机组从210 MW至330 MW这17个工况点下的煤耗量。之后再进行迭代计算,当前后两次所得出的热力数据小于某一极小量时,可结束迭代计算过程。迭代结束后,进行机组和全厂的热经济性指标计算。
3 等微增算法和动态规划算法的比较 3.1 两种算法结果类似用反平衡计算得出某电厂3台300 MW机组不同负荷下煤耗量见表 1。根据表 1中数据分别进行等微增和动态规划计算,并对计算结果进行比较,得出机组间负荷最优分配结果,即3台300 MW机组总负荷为700 MW,则每台机组的负荷为多少才能使得电厂总煤耗量最小。
| 表 1 某电厂300 MW机组不同负荷下煤耗量 |
(1)用动态规划算法计算,结果为当1号机组分配215 MW,2号机组分配245 MW,3号机组分配240 MW,全厂的总煤耗量最小,为220.79 t/h。
(2)用等微增法计算,结果为当1号机组分配253.2 MW,2号机组分配230.1 MW,3号机组分配216.7 MW,全厂的总煤耗量为最小。
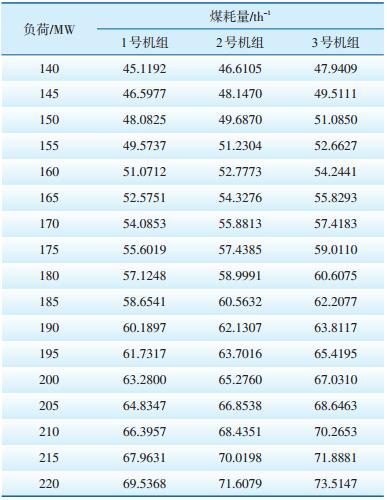
3.2 两种算法结果不同有时用动态规划法进行负荷最优分配会得出两种不同的分配方案。例如某电厂有3台200 MW机组,当该电厂需输出负荷500 MW时,电厂每台机组需要负荷多少使总煤耗最小。该电厂机组煤耗量如表 2所示。
| 表 2 某电厂200 MW机组不同负荷下煤耗量 |
(1)用动态规划发进行负荷最优分配会得出2个分配方案。方案1:1号机组负荷190 MW,2号机组负荷165 MW,3号机组负荷145 MW;方案2:1号机组负荷200 MW,2号机组负荷160 MW,3号机组负荷140 MW。这就给火力发电厂机组负荷优化分配带来了不稳定因素和困扰。
(2)用等微增算法进行负荷最优分配则不会得出2种结果。将表 2中数据拟合得可以到3台机组的耗量特性方程:

|
(7) |

|
(8) |

|
(9) |
根据特性方程计算得出1个分配方案,即1号机组负荷198.5 MW,2号机组负荷161.6 MW,3号机组负荷140 MW。
动态规划算负荷分配时会出现2种结果,而等微增仅有1种结果,是因为等微增算法需进行数据拟合,而动态规划则不进行拟合,直接利用数据计算得出结果。
3.3 数据拟合后再进行动态规划计算3.2中提到动态规划计算中出现2个结果是因为数据没有经过拟合,为了进一步证实,现将表 2的数据进行拟合得到表 3。
| 表 3 200 MW机组不同负荷下煤耗量拟合后结果 |
应用动态规划法将以上拟合后的数据进行负荷分配,原来的2套分配方案变成了1套方案,即:1号机组负荷200 MW,2号机组负荷160 MW,3号机组负荷140 MW。该方案和等微增的负荷分配结果(1号机组负荷198.5 MW,2号机组负荷161.6 MW,3号机组负荷140 MW)非常接近。同样如果将表 1的数据拟合后再进行动态规划计算可得到机组的最优分配方案为:1号机组负荷255 MW,2号机组负荷230 MW,3号机组负荷215 MW,这与等微增分配方案(1号机组负荷253.2 MW,2号机组负荷230.1 MW,3号机组负荷216.7 MW)也十分接近。
4 结论通过以上对动态规划和等微增两种算法在火力发电厂机组负荷分配中应用的对比可以看出,传统的动态规划算法所得到的分配方案的最优解并不唯一,这是一个不稳定的结果,而将数据拟合后再应用动态规划计算则结果唯一。经分析,拟合后的动态规划算法所得到的结果趋近于等微增的结果,将数据拟合之后的动态规划算法应用于电厂机组负荷分配更加科学,拟合后的动态规划算法与等微增的算法实质相同。
| [1] | 郭民臣. 电厂热力系统分析方法的研究与发展现状[J]. 热力发电, 2001(6): 7–9. |
| [2] | 郑体宽. 热力发电厂[M]. 北京: 中国电力出版社, 2008. |
| [3] | 张维存, 陈树新, 黄重国. 发电厂机组组合与负荷分配[J]. 中国制造业信息化, 2005, 34(6): 85–86. |
| [4] | 董宇翔, 吕丽霞. 发电厂机组组合负荷优化分配算法的分析[J]. 科技创新导报, 2011(34): 95–96. DOI:10.3969/j.issn.1674-098X.2011.34.076 |
| [5] | 郭民臣, 魏楠. 火电机组性能监测与小指标在线考核管理系统在电厂运行优化方面的应用[J]. 电力设备, 2007(2): 12–15. |
| [6] | 郑桂林, 专祥涛. 火电厂机组负荷最优分配软件开发[J]. 中国电力, 2003, 36(10): 31–33. DOI:10.3969/j.issn.1007-3361.2003.10.015 |
| [7] | 李鹏. 等微增率准则在机组负荷优化分配中的应用条件[J]. 南方电网技术, 2008(10): 43–50. |
| [8] | 史国青. 火电厂机组负荷优化组合分配问题的研究[D]. 北京: 华北电力大学, 2005. |
| [9] | 刘严, 谭忠富. 动态规划方法在机组负荷最优分配中的应用[J]. 现代电力, 2003(2): 76–80. |
| [10] | 杨勇平, 王加璇. 火电机组耗量特性的在线确定与机组间负荷最优分配[J]. 电站系统工程, 1995, 11(3): 18–27. |
 2017, Vol. 35
2017, Vol. 35