叶片是汽轮机中最重要的零部件之一,承担着将蒸汽热能转化为机械能的主要任务,在运行中承受着离心力、稳态气流力及非稳态气流力的共同作用[1-3]。随着叶片结构及工作环境复杂化,其振动及由此引发的振动超标、磨损、疲劳失效等故障也越来越突出[4-6]。在汽轮机叶片的振动和噪声控制中,阻尼特性可以客观反映叶片结构系统振动过程中能量耗散的速度,因而越来越受重视。但叶片阻尼机理较复杂,通常会受边界约束条件、激励幅度、背景噪声及环境温度等因素的影响,使阻尼的测量具有很大的不确定性[7]。到目前为止,学术及工程界尚未建立一种完备而有效的阻尼评价与测试方法。在阻尼测试的实践中,经常出现精度低、可重复性差及测试效率低下等缺陷,因此,关于阻尼测试的研究还应进一步深入。
目前,用于描述汽轮机叶片阻尼的参量有很多,包括相位差角、对数衰减系数、品质因子、损耗因子等[8]。人们一般通过时域、频域两类阻尼测试方法获取汽轮机叶片阻尼比。例如Srinivasan和Cutts对具有凸肩阻尼结构的汽轮机叶片进行了测试,并分析了摩擦接触面切向刚度对阻尼特性的影响[9]。Rao和Vyas考虑了非线性阻尼的影响,并通过实验研究了汽轮机叶片应力与汽轮机转速之间的定量关系,研究结果表明,其各阶阻尼比随着转速的上升呈减小的趋势[10]。Allara等人测试了汽轮机叶片在不同振幅和离心载荷下的阻尼比,发现其振幅越大,离心载荷越小,叶片的阻尼测试结果就越大[11]。陈茉莉和李舜铭针对转子叶片动态设计中阻尼比难以估计的问题,建立了分布激励下转子叶片的响应模型,并基于此模型设计了1种分布激励突卸的非接触阻尼比试验方法,同时利用半功率带宽法获得了转子叶片的前8阶阻尼比[12]。谢永慧等人对具有阻尼围带和凸台拉筋特征的汽轮机长叶片进行了测试,获得不同转速正压力下叶片的频响曲线和模态阻尼比[13]。周显丁等人搭建了带有干摩擦阻尼的叶片振动测试平台,通过测试获得叶片在不同激振力及模拟离心力转速下的模态阻尼比[14]。
从当前可掌握的文献资料来看,虽然人们针对汽轮机叶片结构的阻尼特性开展了大量研究,但许多文献在采用包络线或对数衰减法获取阻尼时,并没有考虑时域衰减信号的不同衰减时刻对阻尼参数的影响。基于时域衰减信号获得叶片阻尼具有很大的不确定性,因此,有必要对该问题进行更深入研究。
1 测试方法概述本文设计了一种汽轮机叶片阻尼特性的测试方法。首先,组建汽轮机叶片阻尼测试系统,提出阻尼不确定性测试流程,并通过标准差指标量化表征某一阶阻尼的不确定性程度;然后,以3种不同类型的汽轮机叶片为研究对象,通过测试获取其在不同衰减时刻的阻尼比,并证明其阻尼确实存在不确定性;最后,分析激励幅度、悬臂边界条件、背景噪声对叶片某一阶阻尼的不确定性的影响程度和影响规律,并采用线性平均法将自由衰减信号中多个衰减时刻对应的阻尼比的平均值作为最终的某阶模态阻尼结果。
2 测试对象及测试系统 2.1 测试对象基于时域衰减信号进行阻尼不确定性测试,测试对象分别为A、B、C 3种不同类型的叶片,其实物图如图 1所示。

|
图 1 3种不同类型的汽轮机叶片 |
为了精确有效地获取汽轮机叶片的阻尼比,采用模态力锤来对其进行脉冲激励,利用金盾电磁振动台对其进行扫频和定频激励,并通过非接触激光测振仪获取其振动响应信号。同时,使用LMS数据采集仪和移动工作站对激励信号和响应信号进行实时采集和分析处理。图 2为获取汽轮机叶片阻尼搭建的测试系统图。

|
图 2 汽轮机叶片阻尼测试系统 |
从时域角度进行汽轮机叶片阻尼不确定性测试,首先要获得汽轮机叶片的各阶固有频率。可通过锤击法获得各阶固有频率的大致范围,再利用振动台对其进行扫频激励,以准确获取各阶固有频率。然后采用定频共振激励,待汽轮机叶片达到稳态响应后停止激励,并用非接触激光测振仪测量时域衰减信号。最后,通过包络线法获得该信号在不同衰减时刻对应的阻尼比,并对其不确定性进行评价。具体步骤如下。
3.1 确定边界条件及测点位置为了模拟汽轮机叶片的装配方式,测试采用悬臂约束边界条件。首先通过夹具将叶片固定在工作台上,并通过力矩扳手确定夹具夹紧螺栓的力矩,以一定力矩拧紧A、B、C型叶片进行测试。
为了使振动响应较强且不超出激光测振仪的量程,经过反复测试对比,测点位置选取叶尖处。
3.2 通过锤击法初步获得汽轮机叶片固有频率使用模态力锤对汽轮机叶片进行脉冲激励并获得力信号脉冲,同时使用非接触激光测振仪获得响应信号。采用LMS软件分析频响函数峰值所对应的频率,初步获得汽轮机叶片的固有频率。
3.3 通过扫频法精确获得汽轮机叶片固有频率采用振动台以基础激励的方式对悬臂汽轮机叶片结构进行定幅扫频激励,扫频区间可选择锤击获得的某阶固有频率的75%~125%,在此频段内以能够有效消除瞬态振动的扫频速度(通常 < 1 Hz/s)进行扫频测试;用激光测振仪采集响应信号,并对时域原始数据进行分时段FFT变换处理,通过辨识响应峰值来精确识别汽轮机叶片的各阶固有频率。
3.4 获取时域衰减信号在精确获得汽轮机叶片各阶固有频率的基础上,通过振动台以某阶固有频率定频、定幅激励汽轮机叶片,待叶片结构达到稳态响应后停止激励,同时使用激光测振仪记录该阶固有频率激励下的时域衰减信号。
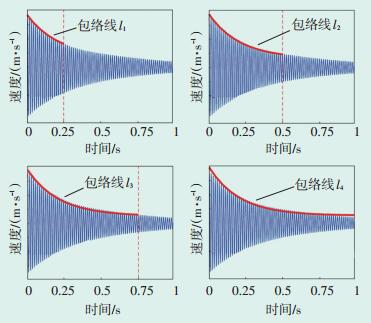
3.5 通过包络线法获得阻尼测试时,汽轮机叶片时域衰减信号的总衰减时长并不相同(受到激励幅度、模态阶次、边界条件等因素的影响),为了便于比对阻尼测试结果,分别设定了4个固定的衰减时刻t1、t2、t3、t4,并在4个衰减时刻通过包络线法获得汽轮机叶片的阻尼结果。图 3为某次测试获得的不同衰减时刻对应的包络线图,t1、t2、t3、t4分别设定为0.25 s、0.5 s、0.75 s、1 s,不同衰减时刻所对应的包络线分别为l1、l2、l3、l4。
|
图 3 汽轮机叶片衰减信号在不同衰减时刻的包络线图 |
在4个固定的衰减时刻t1、t2、t3、t4,采用包络线法获得汽轮机叶片在某一阶模态的阻尼比ξ1、ξ2、ξ3、ξ4后,通过线性平均方法将上述4个阻尼比的平均值作为最终的某阶模态阻尼比。进一步求取上述4个衰减时刻对应阻尼比的标准差,以量化表征某一阶阻尼的不确定性程度,科学地评价其阻尼的不确定性。
4 测试结果确认 4.1 A型叶片对A型叶片进行测试,获得的前6阶固有频率如表 1所示。
| 表 1 A型叶片前6阶固有频率 |
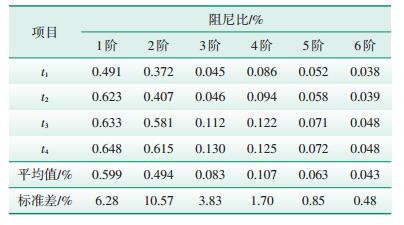
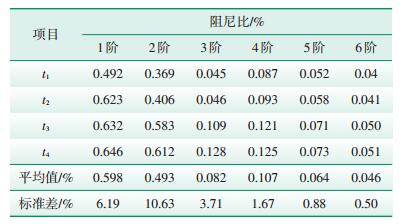
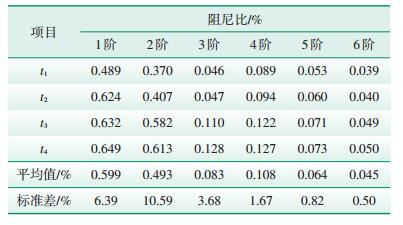
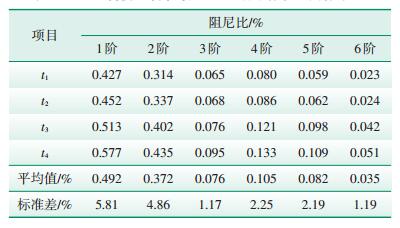
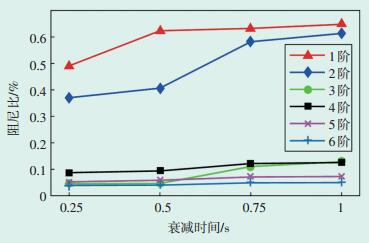
获取A型叶片在不同衰减时刻对应的阻尼参数,其中4个固定的衰减时刻t1、t2、t3、t4分别设定为0.25 s,0.5 s,0.75 s,1 s。为证明A型叶片阻尼的不确定性是客观存在的,对A型叶片进行3次重复测试。表 2—表 4为3次测试中A型叶片在不同衰减时刻辨识出的阻尼比及其标准差。图 4为A型叶片的前6阶模态在不同衰减时刻所对应的阻尼比(图中的阻尼比为3次测试结果的平均值)。
| 表 2 A型叶片第1次阻尼比测试结果及其标准差 |
| 表 3 A型叶片第2次阻尼比测试结果及其标准差 |
| 表 4 A型叶片第3次阻尼比测试结果及其标准差 |
|
图 4 A型叶片在不同激励幅度下的第3阶阻尼比变化曲线 |
根据A型叶片的3次阻尼测试结果可以看出,各阶阻尼比对应的标准差在0.48%~10.63%。由此可知,由于不同衰减时刻的差异,会产生阻尼结果的不确定性。同时,3次测试获得的阻尼比及标准差均比较接近,证明A型叶片阻尼不确定性的存在不是偶然现象。
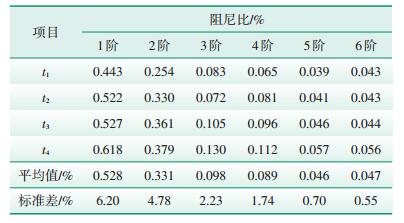
4.2 B型和C型叶片选取与A型叶片不同类型的B、C型叶片,各进行1次阻尼测试并比对。表 5、表 6为B型和C型叶片在不同衰减时刻辨识出的阻尼比及其标准差。
| 表 5 B型汽轮机叶片的阻尼比测试结果及其标准差 |
| 表 6 C型汽轮机叶片的阻尼比测试结果及其标准差 |
根据B型和C型叶片的测试结果可以看出,他们在不同衰减时刻获得的阻尼比不相同,各阶阻尼比对应的标准差在0.70%~6.20%,进一步说明,从时域角度测试汽轮机叶片阻尼,确实存在不确定现象。
5 影响因素分析本节以A型叶片为试验对象,分析激励幅度、悬臂边界条件及背景噪声等因素对其阻尼不确定性的影响规律。
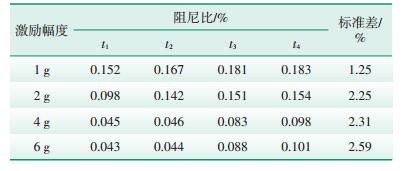
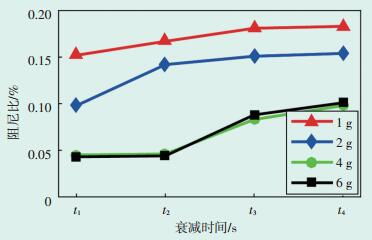
5.1 激励幅度选取1 g、2 g、4 g、6 g 4个激励幅度,以A型叶片的第3阶固有频率对其进行定频激励,待达到稳态响应后停止激励,获取其时域衰减信号。表 7为该表 5 B型汽轮机叶片的阻尼比测试结果及其标准差信号在不同衰减时刻所对应的第3阶阻尼比及其标准差,图 5为不同激励幅度下其阻尼比的变化曲线(其中4个不同的衰减时刻t1、t2、t3、t4分别设定为0.25 s、0.5 s、0.75 s、1 s)。
| 表 7 C型汽轮机叶片的阻尼比测试结果及其标准差 |
|
图 5 A型叶片在不同激励幅度下的第3阶阻尼比变化曲线 |
对上述结果进行分析可知,A型叶片第3阶阻尼比的标准差在1.25%~2.59%,且随着激励幅度的增加,其阻尼的不确定性程度在逐渐增大。同时,随着衰减时间的持续和激励幅度的减小,其阻尼比呈现出逐步增大的趋势,这种现象是汽轮机叶片经过热喷涂处理,涂层带有镍铬碳化合物,导致其阻尼具有振幅依赖性造成的。
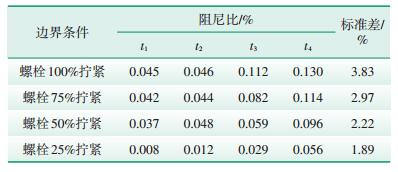
5.2 悬臂边界条件首先,使用50 Nm的力矩拧紧A型叶片夹具上的4个M8螺栓,并通过力矩扳手调整螺栓的拧紧力矩,以模拟不同悬臂边界条件。然后,分别在螺栓100%、75%、50%、25%拧紧条件下,依次进行阻尼测试。表 8为不同悬臂边界条件下A型叶片第3阶阻尼比及其标准差。
| 表 8 不同悬臂边界条件下A型叶片第3阶阻尼比及其标准差 |
根据A型叶片在不同悬臂边界条件下的测试结果可以看出,其第3阶阻尼比的标准差在1.89%~ 3.85%,且随着悬臂边界条件约束能力降低,其标准差也逐渐减小,即阻尼的不确定性程度在逐步减小。这可能是悬臂边界条件的弱化导致阻尼性能降低,因而在不同的衰减时刻,A型叶片对应的阻尼结果差别变小所致。
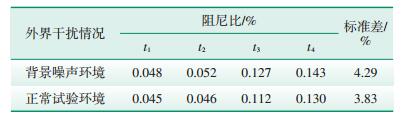
5.3 背景噪声在测试中发现汽轮机叶片的时域衰减信号很容易受到背景噪声的干扰,因此在测试系统中增加高压空气激励所带来的背景噪声的影响,并分别在正常试验环境和背景噪声环境下,对A型叶片的第3阶阻尼进行测试,表 9为2种环境下获得的第3阶阻尼比及其标准差。
| 表 9 有无背景噪声下A型叶片第3阶阻尼比及其标准差 |
根据表 9测试结果可以看出,A型叶片在有背景噪声的环境下,其第3阶阻尼比对应的标准差为4.29%,大于正常试验环境下的标准差,因此可知汽轮机叶片的阻尼会受到背景噪声的影响,且阻尼不确定性的程度会随着背景噪声的增大而增大。
6 结语通过对汽轮机叶片开展的一系列阻尼测试试验可知,其阻尼确实存在不确定性现象,且其不确定性的程度受激励幅度、悬臂边界条件、背景噪声的影响。为解决不确定性带来的阻尼参数辨识问题,本文提出了线性平均方法,该方法操作方便、原理简洁易懂,能够快速获取某一阶阻尼参数,并在一定程度上降低背景噪声信号对测试结果的影响。
随着汽轮机组单机功率的增大,尤其是近来超超临界机组的发展,末几级叶片越来越长,相应地降低了叶片的刚性,不但使叶片运行时扭转恢复角增大,同时也降低了叶片抵抗振动应力的能力,因此通过阻尼特性测试方法分析各种叶片阻尼结构可以提高叶片抵抗振动疲劳的能力。本文提出的叶片阻尼特性测试方法对叶片阻尼特性的研究及制造具有参考价值。
| [1] | Csaba G. Modelling Microslip Friction Damping and Its Influence on Turbine Blade Vibration[D].Linkoping:University of Linkoping, 1998. |
| [2] | 丁有余, 周宏利, 徐铸, 等. 汽轮机强度计算[M]. 北京: 水利电力出版社, 1985. |
| [3] | 赵子辉, 谢永慧. 汽轮机叶片结构阻尼研究发展现状及展望[J]. 汽轮机技术, 2008, 50(1): 1–5. |
| [4] | Cigeroglu E, OzguvenH N. Nonlinear Vibration Analysis of Bladed Disks with Dry Friction Dampers[J]. Journal of Sound and Vibration, 2006, 295(3): 1028–1043. |
| [5] | 王玉武. 200 MW机组中压转子末级叶片拉筋改进[J]. 汽轮机技术, 2002, 44(4): 242–245. |
| [6] | 杨凌云, 郭勇, 王振林. 汽轮机叶片振动疲劳试验振幅的DSCM实时监测技术[J]. 汽轮机技术, 2006, 48(3): 206–208. |
| [7] | 谢永慧, 张荻. 汽轮机阻尼围带长叶片振动特性研究[J]. 中国电机工程学报, 2015, 5(18): 86–90. |
| [8] | 戴德沛. 阻尼技术的工程应用[M]. 北京: 清华大学出版社, 1991: 40-48. |
| [9] | Srinivasan AV, CuttsDG. Dry Friction Damping Mechanisms in Engine Blades[J]. Journal of Engineering for Gas Turbines & Power, 1983, 105(2): 332. |
| [10] | Rao JS, Vyas NS. Determination of Blade Stresses under Constant Speed and Transient Conditions with Nonlinear Damping[J]. Journal of Engineering for Gas Turbines & Power, 1996, 118(2): 424–433. |
| [11] | Allara M, FilippiM, Gola MM. An Experimental Method for the Measurement of Blade-Root Damping[J]. Asme Turbo Expo:Power for Land, Sea & Air, 2006(61): 514–518. |
| [12] | 陈茉莉, 李舜酩. 基于分布激励突卸的转子叶片阻尼比试验[J]. 航空动力学报, 2009, 24(11): 2521–2526. |
| [13] | 谢永慧, 吴君, 张荻, 等. 具有整体围带和凸台拉筋汽轮机长叶片阻尼振动特性实验研究[J]. 汽轮机技术, 2011, 53(2): 81–84. |
| [14] | 周显丁, 谢永慧, 吴君. 新型阻尼结构叶片振动特性试验研究[J]. 东方汽轮机, 2011(4): 4–10. |
 2017, Vol. 35
2017, Vol. 35