风能作为一种环境友好型的可再生能源,在世界范围内得到了迅速的发展,已经成为成熟的新能源发电技术之一。与此同时,由于风能的波动性、间歇性等特点,风力发电在电力系统中的高渗透性为电网运营带来了一系列的挑战。对风电场输出功率进行预测,可以为电网发电计划安排、停机检修等提供依据,有利于提高系统的安全可靠性和运行经济性[1-2]。
风电功率预测技术是风力发电技术的重要领域之一。随着电网中风电的渗透比例越来越高,对风电功率预测精度提出了更高的要求,学者们就风电功率预测方法提出了很多预测方法,大致可以分为4类:物理方法、统计方法、人工智能方法和组合预测方法。物理方法是根据天气预报的信息,通过分析天气演变过程来预测风电场的风速和风向,然后根据风机或风电场的功率曲线得到输出功率的预测值[3]。物理方法不需要统计历史数据,但其物理模型的建立非常复杂,求解难度和计算量都很大,难以满足超短期预测的要求。统计方法是根据历史数据进行统计分析,建立系统输入与输出之间的线性或非线性映射,由于历史数据序列反映气象和环境等因素的影响,故基于统计观点的模型可以规避对物理机理掌握不够的困难,其主要方法有持续性模型、移动平均模型和自回归移动平均模型[4]。人工智能方法受自然界规律或生物智能方法的启发,设计求解的计算机程序,包括模仿人类思维中模糊性概念的模糊算法,模仿生物进化和群体智能的进化算法,模仿大脑结构及其对信息处理过程的人工神经网络 (ANN) 算法。ANN的非线性逼近能力,使其成为风电功率预测中应用最为广泛的人工智能方法,其中又以反向传播ANN (BP-ANN) [5]应用最广,其他方法还有径向基神经网络 (RBF-ANN) [6]、Elman神经网络 (Elman-ANN) [7]及小波神经网络[8]等。此外,支持向量机 (SVM)、遗传算法 (GA)、粒子群算法 (PSO) 等人工智能方法也被用于风电功率的预测。虽然风电功率预测技术的理论和方法已经非常成熟,但单一的预测方法均有其局限性,很难满足目前电网对风电功率的预测精度要求,因此不少学者通过结合2种或多种方法各自的特点,来提高风电功率的预测精度,即建立组合风电功率预测模型。实际上,近年来提出的大部分预测模型都是组合预测方法[9-11]。
针对风电功率时间序列随机性、波动性和非平稳性的特点,分解技术经常被用来发掘其内部特征,进而提高风电功率的预测精度。例如小波包分解 (wavelet packet decomposition,WPD) [12]和经验模态分解 (empirical mode decompose-tion,EMD) [8]分别与ANN结合,可以有效提高风电功率预测精度。但是单一的分解技术均有各自的缺陷,如WPD可以将时间序列精确划分,但不能自适应分解。对跳跃性的时间序列分解时,EMD会产生模态混叠现象。因此有必要把不同分解方法结合起来,以提高分解的有效性。WPD与EMD分解方法的结合已经成功应用到其他领域[13-14],但在风电功率预测领域还没有相关的研究。本文提出一种基于EMD和WPD的组合风电功率预测模型,结合了两者的优点,提高了风电功率的预测精度。
1 基于EMD和WPD的组合分解方法 1.1 EMD基本原理EMD是一种新的信号处理方法,其实质是基于局部特征尺度对一个非线性、非平稳信号进行平稳化处理,将不同尺度的波动或趋势从原来的复杂信号中逐级分解出来,形成一系列具有不同特征尺度的固有模态分量和余项。固有模态分量反映信号的内部特征,余项则表示信号趋势[15]。所有的固有模态分量应满足以下条件:序列的极值点数量与过零点数量相等,或最多相差1个;由信号的局部最大值和局部最小值定义的包络线在任一点的均值均为零。EMD分解步骤如下:
(1) 找出被分析数据X(t) 的全部极大值点和极小值点,用三次样条函数曲线循序连接全部的极大值点和极小值点,得到X (t) 的上下包络线。
(2) 计算上下包络线的均值m(t),将原始数据序列减去m (t),得到1个低频的新数据序列h (t),即h(t) =X(t)-m(t),判断h(t) 是否满足固有模态分量的2个条件,如果满足,那么h(t) 便是第1个固有模态分量,否则将h (t) 作为原始序列。
(3) 重复上述步骤 (1) 和 (2),直到经过i次筛选后hi(t) 满足固有模态分量条件,这样hi(t) 即为第1个固有模态分量,记作C1(t),表示数据序列中最高频的成分。
(4) 用X(t) 减去C1(t),得到1个去掉高频分量的新数据序列r1(t);
(5) 将r1(t) 重复步骤 (1)— (4),得到其余的固有模态分量,直到最后1个rn(t) 不可分解,称为剩余分量最终信号RES,其表达式如下:
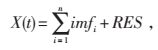
|
(1) |
式中n—固有模态分量的个数;
imfi—第i (i=1, 2, 3, …, n) 个模态函数,分别表示信号从高频到低频不同频段成分。
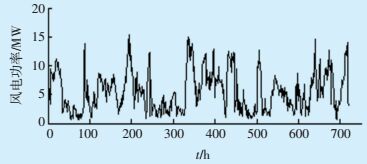
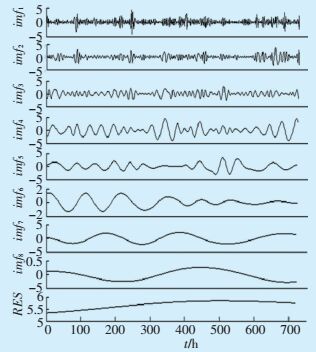
每个频段频率成分不同,并会随着信号不同而变化。图 1和图 2分别为某风电场风电功率原始时间序列和EMD分解后的结果 (n=8)。
|
图 1 某风电场风电功率原始时间序列 |
|
图 2 某风电场风电功率原始时间序列EMD分解结果 |
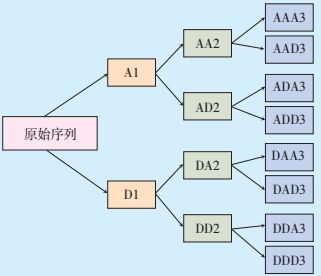
WPD对小波分解进行了改进,能够对信号进行精细分析。它将频带进行多层次划分,不仅对低频分量分解,而且将小波分析中没有细分的高频分量也进一步分解,形成1个完整二叉树结构 (见图 3)。
|
图中:A—低频;D—高频 图 3 WPD分解示意图 |
Matlab小波分析工具箱可以很方便地完成对信号的小波分解及重构。
1.3 基于EMD和WPD的组合分解方法EMD在实际应用中还存在许多不足,其中端点效应、固有模态分量筛分迭代停止的标准和模态混叠是最重要的3个问题[16]。模态混叠问题对信号的建模和预测有很大的影响,使得信号预测很难取得较好的结果[17]。文献[16]提出了基于WPD的EMD方法,将WPD的多分辨分析扩展到EMD的模态混叠序列中,以提高EMD的分解能力。本文将这一组合分解方法运用到风电功率的预测中,利用WPD对EMD分解后的高复杂度序列进行二次分解,以提高风电功率的预测精度。
2 样本熵样本熵是在近似熵的基础上改进的一种复杂度计算方法,它不仅具备近似熵的所有优点,而且避免了近似熵中统计量的不一致性[18]。其算法如下:
(1) 将原始数据按连续顺序组成一组m维矢量:
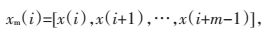
|
(2) |
其中,i∈[1,N-m],N为原始序列的维数。
(2) 定义xm(i) 和xm(j) 之间对应元素中差值的最大值d[xm (i),xm (j)],即
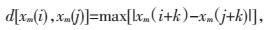
|
(3) |
其中,k∈[0,m-1];i,j∈[1,N-m],j≠i。
(3) 给定阈值r,对每个i≤N-m的值,统计d[xm(i),xm(j)]小于r的数目,并计算该数目与距离总数N-m-1的比值,记作Brm (i)= Nm(i)/(N-m-1)。求其对i的平均值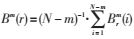
(4) 将维数增加1,即对m+1维矢量重复步骤 (1) — (3),得到Bm+1(r)。
理论上此序列的样本熵为:
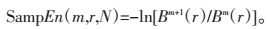
|
(4) |
不同的嵌入维数m和阈值r对应的样本熵不同。一般情况下,当m=1或2,r= (0.10~0.25) Estd(Estd为原始数据的标准差) 时,计算得到的样本熵具有较合理的统计特性。因此本文取m=2,r=0.2Estd,计算某风电场EMD分解风电功率序列得到的子序列样本熵如表 1所示。根据样本熵及风电功率子序列的波动情况,把imf1和imf2作为高复杂度子序列,imf3~imf6为适中复杂度子序列,imf7、imf8和RES为低复杂度序列。
| 表 1 EMD分解后风电功率子序列样本熵 |
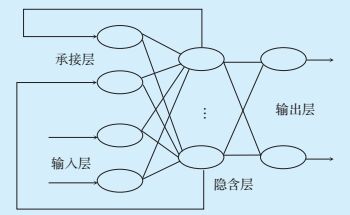
Elman神经网络是典型的动态回归神经网络,由输入层、隐含层、输出层以及承接层构成。它在BP神经网络基础上,将隐含层的输出通过承接层的储存和延迟连到输入层的输入。输入层单元的作用是传递信号,输出层单元的作用是线性加权。隐含层单元的传递函数可以使用线性函数或非线性函数,承接层可将隐含层单元前一时刻的输出值作为下一时刻的输入值。与BP神经网络相比,Elman神经网络具有更强的动态行为和计算能力,利于建立时间序列的预测模型。Elman神经网络的结构如图 4所示。
|
图 4 Elman神经网络结构 |
纵横交叉算法 (crisscross optimization algo-rithm, CSO) 是一种全新的群体智能优化算法。其搜索行为由横向交叉和纵向交叉两部分组成。横向交叉进行全局搜索,纵向交叉进行小概率突变筛选,每次迭代两种算子交替进行,通过贪婪选择机制使交叉后的子代与父代竞争,产生占优解,加快算法的收敛速度[19]。
3.3 CSO优化Elman神经网络Elman神经网络在预测过程中,采用梯度下降法调整权值和阈值,容易陷入局部最优,而且当影响因素和学习样本增多时,神经网络的计算量和权值将急剧增加,导致收敛速度慢。
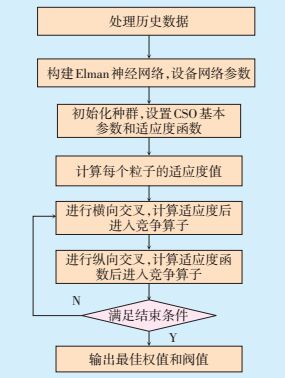
CSO结合横向交叉的全局寻优能力和纵向交叉的变异更新能力,可以克服Elman神经网络固有的缺点。CSO优化Elman神经网络的基本思想是利用CSO替代Elman神经网络的沿梯度反向传播训练,寻找最佳权值和阀值。CSO优化Elman神经网络的流程图如图 5所示。
|
图 5 CSO优化ELman神经网络流程图 |
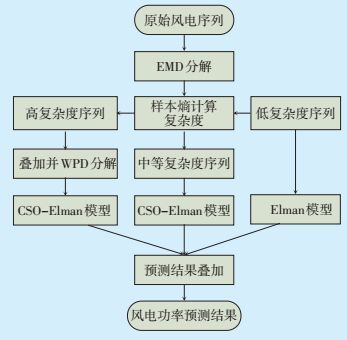
本文提出一种基于EMD和WPD的组合分解方法。首先使用组合分解方法对风电功率时间序列进行分解,然后使用Elman神经网络对各个序列进行预测,即建立EMD-WPD-Elman预测模型。为了进一步提高预测精度,采用CSO优化Elman神经网络的权值和阈值,即建立EMD-WPD-CSO-Elman预测模型。具体步骤如下:首先利用EMD将不平稳的风电功率分解为一系列具有不同特征尺度的子序列;然后利用样本熵对不同尺度的子序列进行复杂度分析,根据子序列不同的熵值,将其进行归类。复杂度低的序列趋势比较明显,平稳性高,可建立Elman预测模型;复杂度适中的序列波动性较大,利用CSO优化Elman神经网络,以提高预测精度,建立CSO-Elman预测模型;复杂度高的序列存在严重的模态混叠问题,故将其叠加在一起,利用WPD进行二次分解并重构,产生一系列较为平稳的序列,建立CSO-Elman预测模型。最后叠加各个序列的预测结果,得到最终的风电功率预测结果。具体流程图如图 6所示。
|
图 6 风电功率预测流程图 |
为了验证本文方法的有效性,分别建立EMD-Elman、WPD-Elman、Elman预测模型与本文模型进行比较,结果证实本文模型的预测精度明显优于其他模型。
5 算例分析 5.1 试验设计本文以某风电场1月份实际采集的风电功率时间序列作为试验数据样本。该风电场的额定装机容量为20 MW,输入样本为每1 h采样1个点,采用前25日数据进行模型训练,即前600个点为训练样本,第26日的数据为测试样本。采用一步滚动预测的方式预测未来24 h的风电功率,即进行24次单步预测。具体方法为:前600个点执行一次预测后,将预测得到的结果加入训练样本,同时将前一次训练样本的第1个数据去掉,即每次训练样本取预测时刻的前600个数据,再执行1次预测,得到下一时刻的预测值。如此反复24次即可得到26日1 d的风电功率预测结果。所有仿真均在Matlab应用软件中进行。
5.2 预测评价指标为全面有效地评价各模型的预测结果,分别采用绝对平均误差 (MAE)、平均相对百分比误差 (MAPE) 和均方根误差 (RMSE) 评价各模型的预测性能。
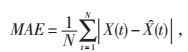
|
(5) |
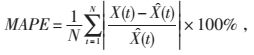
|
(6) |
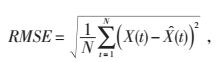
|
(7) |
式中N—测试的时间点数,N=24;
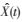
X(t)—t时刻风电功率预测值。
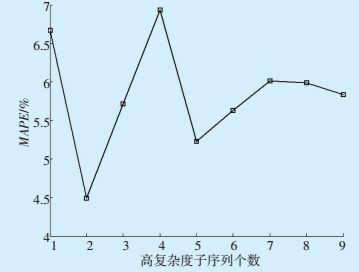
采用EMD-WPD-Elman模型对高复杂度子序列含有不同imf个数的MAPE的对比分析如图 7所示。可以看出,高复杂度子序列含有2个imf的预测效果最优。采用同样的方法可以确定中等复杂度序列的个数为3。复杂度的划分与图 2所示的风电功率子序列的波动情况相吻合,证明了利用样本熵可以衡量风电序列的复杂度。
|
图 7 高复杂度子序列MAPE对比 |
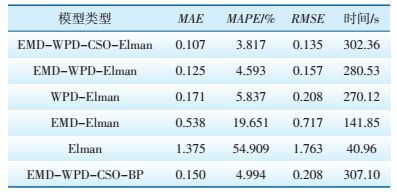
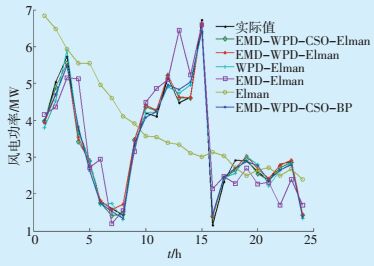
分别使用EMD-WPD-CSO-Elman、EMD-WPDCSO-BP、EMD-WPD-Elman、WPD-Elman、EMD-El-man、Elman对第26日风电功率进行预测,预测时间分辨率为1 h。各模型的预测结果如图 8所示,所有模型的预测误差分析及运算时间如表 2所示。
|
图 8 某风电场第26日风电功率预测结果对比 |
| 表 2 各模型预测结果比较 |
从图 8中可以观察到,EMD-WPD-CSO-Elman模型提前24 h的风电功率预测值与实际值吻合最好,而Elman神经网络预测结果与实际值相差很大。这是因为Elman一步预测效果较差,预测结果作为下一步训练样本时包含的有用信息少,使下一步的预测结果误差也较大。采用分解方法后预测精度有了很大提高,这是因为分解之后的序列可以更好地找出数据内在的趋势和规律,大大提高了一步预测精度。虽然一步预测结果有一定的误差,但误差很小,且在允许范围内,没有破坏数据内在的趋势和规律,可以作为下一时刻的训练样本。采用分解方法之后的模型在风电功率变化较大时能够更快地做出反应,使预测曲线更好地跟踪实际功率曲线。
分析表 2可知:
(1) 对比EMD-Elman、WPD-Elman与Elman模型,采用分解算法的模型具有更好的预测精度;
(2) 对比EMD-WPD-Elman、EMD-Elman与WPD-Elman模型,前者明显具有更高的预测精度,说明组合分解方法的预测模型能够有效提高预测精度;
(3) EMD-WPD-CSO-Elman模型预测精度高于EMD-WPD-CSO-BP,是所有模型中表现最好的,MAE、MAPE、RMSE均取得了理想的结果,分别为0.107、3.817%、0.135,说明使用CSO优化Elman神经网络的参数,可以有效提高神经网络的泛化能力和预测精度;Elman神经网络由于承接层的引入,提高了网络的动态学习能力,比BP神经网络更适用于风电功率预测。
(4) 由于每次都要进行24次的迭代预测,模型的运算时间有所增加,分解算法和优化算法的引入进一步延长了模型的运算时间,但所消耗的时间是可以接受的。
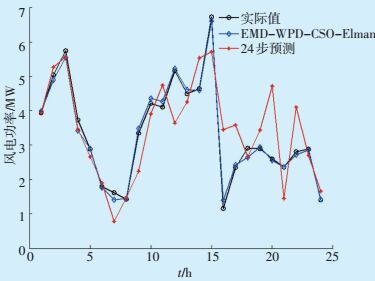
5.4 EMD-WPD-CSO-Elman滚动预测与一次性24步预测结果对比为了验证本文所用滚动预测方法的有效性,使用EMD-WPD-CSO-Elman预测模型分别进行滚动预测和一次性24步预测的结果对比。如图 9所示,滚动预测可以很好地跟踪风电功率的趋势,而一次性24步预测前期预测效果很好,但随着时间的增加误差呈增大趋势,到后期甚至没有预测到风电的变化趋势。这是因为风电波动具有一定的相关性,一次性24步预测前期预测值和临近的实测值相关性较强,因此预测精度较好;而随着预测步长的增加,这种相关性逐渐降弱,预测误差也会随之增大。一次性24步预测最后2 h的预测结果和实际值很接近,这是由预测的随机性造成的,预测结果的后半段并没有很好地跟踪实际风电功率的变化趋势。
|
图 9 EMD-WPD-CSO-Elman滚动预测与一次性24步预测结果对比 |
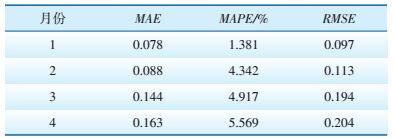
为了进一步测试EMD-WPD-CSO-Elman模型的性能,另外选取同一风电场其他月份的风电功率序列数据,同样对每个月第26日风电功率进行提前24 h预测,预测误差分析如表 3所示。
| 表 3 其他月份误差分析 |
由表 3可知,EMD-WPD-CSO-Elman模型在不同月份均能取得较高的预测精度,最大平均绝对误差为5.569%,最小平均绝对误差为1.381%,5 d的平均值为4.052%,充分说明该模型具有较强的稳定性和泛化能力。
6 结论风电功率的非线性和非平稳性特征难以把握,利用简单的预测模型预测风电功率很难得到理想的预测效果。本文提出了一种基于EMD和WPD的新型风电功率组合预测模型。经实例分析得到以下结论:
(1) 分解算法可以有效降低风电功率的非平稳特性,提高可预测性。
(2) EMP与WPD组合的分解方式有效克服了模态混叠问题对功率预测的影响,提高了预测精度。同时,采用CSO优化Elman神经网络的参数,可以进一步提高风电功率的预测精度。
(3) 滚动预测可有效利用预测信息,提高预测的精度。
| [1] | 张丽英, 叶廷路, 辛耀中, 等. 大规模风电接入电网的相关问题及措施[J]. 中国电机工程学报, 2010(25): 1–9. |
| [2] | 周双喜, 王海超, 陈寿孙. 风力发电运行价值分析[J]. 电网技术, 2006(14): 98–102. DOI:10.3321/j.issn:1000-3673.2006.14.019 |
| [3] | 王丽婕, 冬雷, 高爽. 基于多位置NWP与主成分分析的风电功率短期预测[J]. 电工技术学报, 2015, 30(5): 79–84. |
| [4] | Ait Maatallah O, Achuthan A, Janoyan K, et al. Recursive wind speed forecasting based on Hammerstein Auto-Regressive model[J]. Applied Energy, 2015(145): 191–197. |
| [5] | 范高锋, 王伟胜, 刘纯. 基于人工神经网络的风电功率短期预测系统[J]. 电网技术, 2008(22): 72–76. |
| [6] | 张靠社, 罗钊. 基于RBF-BP组合神经网络的短期风电功率预测研究[J]. 可再生能源, 2014(9): 1346–1351. |
| [7] | 张靠社, 杨剑. 基于Elman神经网络的短期风电功率预测[J]. 电网与清洁能源, 2012(12): 87–91. DOI:10.3969/j.issn.1674-3814.2012.12.018 |
| [8] | 王贺, 胡志坚, 陈珍, 等. 基于集合经验模态分解和小波神经网络的短期风功率组合预测[J]. 电工技术学报, 2013(9): 137–144. |
| [9] | Liang Z, Liang J, Wang C, et al. Short-term wind power combined forecasting based on error forecast correction[J]. Energy Conversion and Management, 2016(119): 215–226. |
| [10] | Yan J, Li K, Bai E, et al. Time series wind power forecasting based on variant Gaussian Process and TLBO[J]. Neurocomputing, 2016(189): 135–144. |
| [11] | Chitsaz H, Amjady N, Zareipour H. Wind power forecast using wavelet neural network trained by improved clonal selection algorithm[J]. Energy Conversion and Management, 2015(89): 588–598. |
| [12] | 孟安波, 卢海明, 胡函武, 等. 混合小波包与纵横交叉算的风电预测神经网络模型[J]. 太阳能学报, 2015(7): 1645–1651. |
| [13] | 吕永卫, 熊诗波, 林选, 等. 基于小波包和EMD处理的滚动轴承故障诊断[J]. 太原理工大学学报, 2010, 41(2): 178–182. |
| [14] | 王红军, 万鹏. 基于EEMD和小波包变换的早期故障敏感特征获取[J]. 北京理工大学学报, 2013, 33(9): 945–950. |
| [15] | Huang W, Shen Z, Huang N E, et al. Engineering analysis of biological variables:an example of blood pressure over 1 day[J]. Proceedings of the National Academy of Sciences, 1998, 95(9): 4816–4821. DOI:10.1073/pnas.95.9.4816 |
| [16] | 刘小峰, 秦树人, 柏林. EMD中存在的问题及解决方法探讨[C]//第九届全国振动理论及应用学术会议论文摘要集. 杭州: 全国振动理论及应用学术会议, 2007. |
| [17] | 刘代志, 钱昌松, 吴晓露, 等. 经验模态分解中模态混叠的若干问题探讨[C]//国家安全地球物理专题研讨会论文集. 厦门: 国家安全地球物理专题研讨会, 2009. |
| [18] | Richman J S, Moorman J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. Ajp Heart & Circulatory Physiology, 2000, 278(6): 2039–2049. |
| [19] | Meng A, Chen Y, Yin H, et al. Crisscross optimization algorithm and its application[J]. Knowledge-Based Systems, 2014, 67(4): 218–229. |
 2017, Vol. 35
2017, Vol. 35