近年来电动汽车由于其零排放的特点成为了应对能源和环境挑战的新型交通工具。随着电动汽车的普及,电动汽车大规模入网将直接导致负荷大量增长,对电力系统规划和运行产生一定影响[1]。
影响电动汽车充电负荷的因素主要分为内部因素和外部因素。内部因素主要包括电动汽车充电时空分布、充电功率、荷电状态、电池特性等,外部因素主要包括用户行驶行为、电价政策和激励措施等。
文献[2]针对不同类型的电动汽车的充电负荷计算方法进行研究,重点在电动汽车充电负荷的发展预测。文献[3]通过概率建模来模拟电动汽车充电功率需求,并针对单辆电动汽车和电动汽车集群的充电负荷进行了对比分析。但是,以上2篇文献均未涉及不同电动汽车充电模式的多样性。文献[4]针对电动汽车时空特性建立了有序充电和无序充电的负荷模型,但是没有给出具体电价策略。文献[5]研究了在电动汽车入网技术(Vehical to grid, V2G)模式下电动汽车充放电成本和效益,基于经济学理论建立了电价优化模型。文献[6]以实时电价为背景提出了优化用户成本和峰谷差的模型,虽然内容涉及电价弹性,但是没有具体讨论其对充电负荷的影响。
目前已有文献涉及电价弹性对电动汽车负荷的影响分析较少,在电网容量约束时,对不同类型用户的响应研究不足。文献[7]利用动态算法求解电动汽车最优调度策略,使用了较为复杂的电池模型和汽车行驶模型,但是对于电价机制方面没有明确说明。
本文针对影响电动汽车负荷的用户行驶行为进行分析,首先根据历史数据和概率模型对电动汽车3种充电方式进行蒙特卡罗模拟,对比了3种充电方式的特点。为了使电动汽车用户主动响应电价政策,研究了经济学电价弹性与负荷需求之间的关系,针对不同用户的响应进行负荷计算,随后建立了优化负荷曲线峰谷差的模型,分析电价弹性对电动汽车充电负荷的影响。
1 电动汽车建模本文研究对象为纯电动私家车,充电方式为常规充电,充电时间由用户的行驶规律和电池特性决定,充电地点一般是社区、充电站等。
电动汽车的日充电负荷与当地的电动汽车数量、电动汽车用户行驶行为和电池特性有关。因此首先对电动汽车用户行驶行为和电池特性进行建模研究。
1.1 电动汽车用户的行驶行为特性用户行驶行为的不确定性是导致电动汽车充电负荷具有不确定性的原因之一。可见,用户的驾驶行为和充电行为将决定调控策略。影响电动汽车充电负荷的用户行为特性主要包括日行驶里程、1 d中最后1次返程时刻、停泊时长等。
1.1.1 行驶里程分布美国能源部电动汽车出行报告(NHTS2009)[4]针对美国家庭交通出行行为做出的调查研究结果表明,电动汽车日行驶里程S分布基本满足对数正态分布,即S~log (μs, σs2),其中,参数μs、σs分别为均值和方差,取决于电动汽车类型和不同城市车辆的行驶规律,其概率密度函数为:

|
(1) |
其中,Ex、Dx为行驶里程的期望和方差,根据不同城市、不同车辆类型的实际统计数据得到;
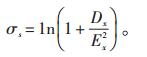
|
电动汽车最后1次返程时刻t0是独立随机变量,满足正态分布t0~N(μt, σt2),其概率密度函数为:
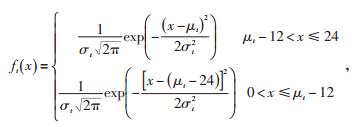
|
(2) |
其中,μt、σt分别为充电起始时间的平均值和方差,受电动汽车类型、充电地点、补贴政策和用户行为习惯综合决定,可以根据实际调查、统计结果给出。本文假设最后1次返程后电动汽车就进行充电。
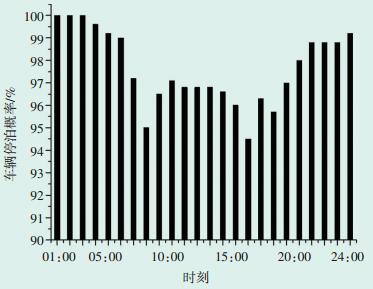
1.1.3 电动汽车停泊时长由于电动汽车只有在停泊时候才可进行充放电,因此电动汽车停泊时长决定了充电时长,也就影响了电网的负荷分布。根据MERGE的研究[8],德国某日不同时刻电动汽车停泊的概率分布如图 1所示。
|
图 1 德国某日不同时刻电动汽车停泊概率 |
电池特性对电动汽车的充放电行为有很大影响,建立合适的电池模型对研究电动汽车充放电负荷十分重要。电池特性主要包括电池容量、荷电状态(state of charge,SOC)和充放电效率等。
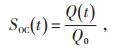
|
(3) |
式中 Q(t)-t时刻电池电量,kWh;
Q0-电动汽车电池容量,kWh。
本文研究常规慢速方式充电,不考虑季节因素,充满电的时间一般不超过6 h,各电动汽车充电功率Pch在2~3 kW服从均匀分布,其概率密度函数fp(x) 为:
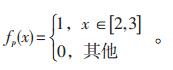
|
(4) |
根据有功负荷的情况,电动汽车充电方式可以分为无序充电、智能充电和V2G等方式[9]。本文假设电动汽车数量为1000辆进行仿真。
2.1 无序充电电动汽车用户在家对电动汽车进行充电,直到电池达到最大荷电状态。这种情况下没有对何时充电、怎样充电进行控制,也不受分时电价等激励措施影响。
由电动汽车日行驶里程和充电接口功率得到充电时长[4]:
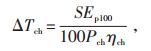
|
(5) |
式中 S-电动汽车日行驶里程;
Ep100-每百千米耗电量;
Pch-慢充充电功率;
ηph-慢充充电效率。
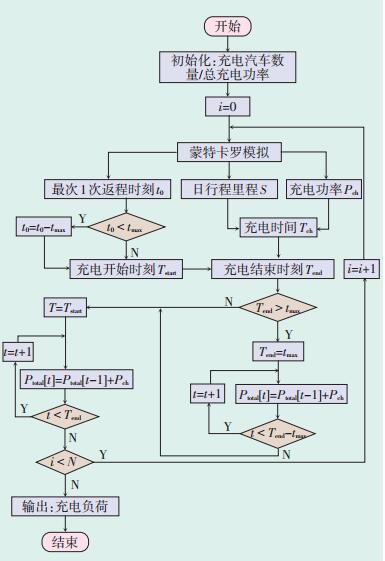
由入网充电时刻和充电时长可以得到单辆电动汽车无序充电日所需功率,由于各辆电动汽车充电时间相互独立,采用蒙特卡罗方法随机抽样模拟[1],由公式(6)累计得到大量电动汽车无序充电日负荷PEVch,算法流程如图 2所示。
|
图 2 无序充电日负荷算法流程 |
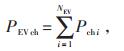
|
(6) |
式中Pchi-第i辆电动汽车充电功率。
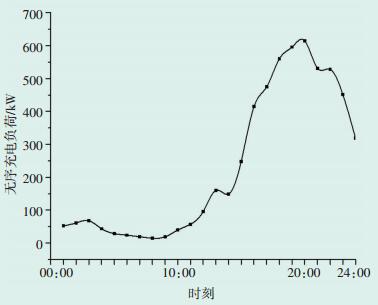
按图 2的算法计算,得到无序充电时电动汽车充电负荷曲线,见图 3。电动汽车在进行无序充电时,充电负荷时间集中在18:00-20:00,与下班回家后充电的行为相符,且日负荷随着电动汽车数量的增加而增加。
|
图 3 电动汽车无序充电日负荷曲线 |
无序充电会对电网造成一定的影响,主要包括线路功率损耗、电压偏移、线路/变压器过载等[10],可通过电价激励措施削峰填谷,使电动汽车充电行为从无序转化为可控。
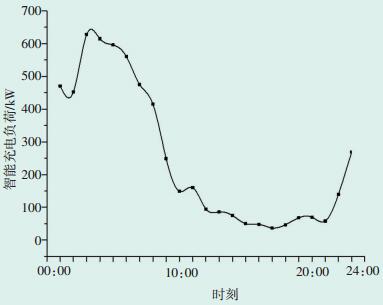
2.2 智能充电的负荷特性建模智能充电是指在大量电动汽车接入的情况下,经电价政策引导,利用间接方式调控电动汽车充电时间,使电动汽车充电负荷能够根据电网负荷削峰填谷[11]。智能充电负荷算法流程类似于无序充电负荷算法流程,只是在充电可入网时间上有所变化,限于篇幅本文不再给出具体流程图。最后得到智能充电日负荷曲线如图 4所示。这种充电方式依靠智能电能表等设备实现电动汽车用户与电网之间信息通信。相比较无序充电,充电负荷高峰出现在夜间,即民用负荷的低谷期,这样一来可在一定程度上平滑电网整体的负荷曲线。
|
图 4 电动汽车智能充电日负荷曲线 |
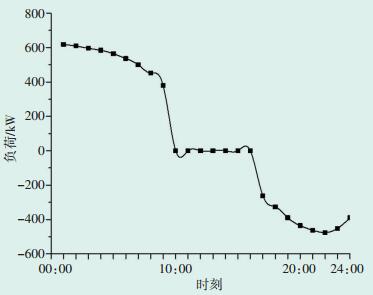
V2G与智能充电方式的不同之处在于除了智能充电的特性,电动汽车还可将电池中储存的电能通过双向功率流放电给电网。假设07:00-17:00时段不进行充放电,对其进行蒙特卡罗模拟,充放电负荷如图 5所示。
|
图 5 电动汽车V2G方式充放电日负荷曲线 |
由图 5可见,与无序充电方式不同的是充电负荷移动到夜间常规负荷低谷并且出现了放电负荷。另外,由于电动汽车向电网放电会给电池带来一定损耗,增加用户电池成本支出,且目前电动汽车入网放电技术尚未普及,因此本文重点讨论智能充电情景。
通过以上的蒙特卡罗模拟算法分析得知,电动汽车在分时电价情况下能发挥削峰填谷的作用,因此,合适的电价模型对负荷优化至关重要。
3 电动汽车充电负荷优化模型 3.1 分时电价Schweppe提出,电能应当被视为具有时空两重差异性的特殊商品[12]。由此,不少学者针对时间、空间变化的电价展开了研究。由于电动汽车充电负荷与常规负荷不同,例如在时间和空间上具有不确定性,规模化的电动汽车充电会给电网的平稳运行带来影响。价格型需求响应是电动汽车有序充电的重要控制策略,合理的电价机制能够激励电动汽车选择合理的时间充电。
峰谷分时电价(time-of-use price, TOU price)是实施需求侧管理的措施之一,用电负荷曲线有着明显的高峰低谷现象,通过划分峰谷时段来确定分时电价,促使电动汽车充电用户自觉调整用电方式,达到削峰填谷的目的,影响负荷曲线的形状[13]。具体来讲,是指根据用户需求与电网不同时段的实际负荷情况,将全天时间划分为峰、平、谷3个时段,对各时段分别制定不同的电价水平,以鼓励用户合理调配用电时间,减轻电网负荷。通常划分为:峰时段8 h(08:00-11:00,18:00-23:00);平时段8 h(07:00-08:00,11:00-18:00);谷时段8 h(23:00-次日07:00)[14]。
3.2 电价弹性需求的电价弹性特征值描述了由于电价变动Δπ引起的电量需求变化量ΔQ,其表达式见公式(7):
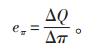
|
(7) |
电能作为一种特殊的商品,其价格可以在不同时段变化从而引导消费者根据实际电价调整负荷需求。电价弹性有2种,即需求的价格弹性(自价格弹性)和交叉价格弹性。
3.2.1 自价格弹性自价格弹性描述了某一时段价格的变动引起的同一时段的电量需求量的变化[15],其值通常为负数,表达式见公式(8):
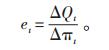
|
(8) |
电价较高时,消费者可根据用电需求减少用电量,将需求电量移至价格较低的时段。
3.2.2 交叉价格弹性某一时段电量需求也可取决于另一时段的电价。由t时刻的电价变动引起的t′时刻需求的变动称为交叉价格弹性[10],其值通常为正数,其表达式见公式(9):
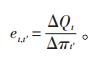
|
(9) |
交叉价格弹性矩阵et, t′由各用户的弹性系数εt, t′组成。理论上,交叉价格弹性矩阵是无损的,即满足式(10):
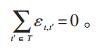
|
(10) |
由自价格弹性和交叉价格弹性引起的需求变动可以求得新的时刻的电量需求[16],其表达式见公式(11):
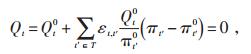
|
(11) |
式中 πt′-优化后电价;
πt′0-t′时刻初始电价;
Qt0-电价调整前充电电量。
式(11)线性化后为:
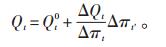
|
(12) |
电动汽车用户对分时电价的响应可能会引发新的充电负荷,即“雪崩效应” [17]。因此设定合适的电价机制来引导电动汽车用户错峰充电可以保证电网安全稳定运行。
本文模型计及电动汽车用户的参与程度,即价格弹性,并且根据上一时段充电负荷结果优化下一时段的电价从而引导这一时段的充电负荷趋优,同时考虑电动汽车基本的约束条件。
3.3.1 目标函数
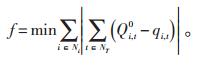
|
(13) |
式中Qi, t0-第i辆车t时段原始负荷需求;
qi.t-电价调整后新的负荷需求。
该目标函数所有电动汽车用户i的原始总负荷Qi, t0和优化后总负荷qi.t之差的绝对值最小,从而达到削峰填谷的目的,尽可能地不削减电动汽车充电负荷,进而优化负荷曲线。
3.3.2 约束条件约束条件(14)使得t时刻的荷电状态不超出上限SOCmax、下限SOCmin,从而满足电动汽车行驶。
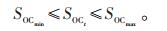
|
(14) |
约束条件(15)使得t时刻总的充电负荷不超过电网传输容量。
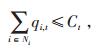
|
(15) |
式中 Ct-电网传输容量。
约束条件(16)设定了电价的最小值:
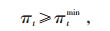
|
(16) |
式中 πtmin-价格下限。
优化后的充电负荷需求qi, t不能超过其最小、最大充电功率,即
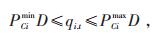
|
(17) |
式中PCimin、PCimax-用户i的充电功率下、上限;
D-充电总时长。
基于式(11),式(18)规定了价格弹性和需求变动之间的关系:
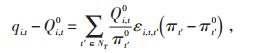
|
(18) |
式中εi, t, t′-单人电动汽车用户交叉价格弹性系数。
3.3.3 求解算法根据模型的线性目标函数及等式约束、不等式约束条件,利用含约束线性求解算法,对模型进行优化求解。
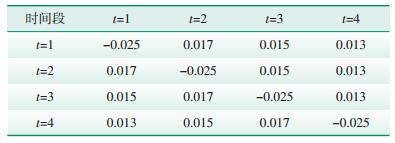
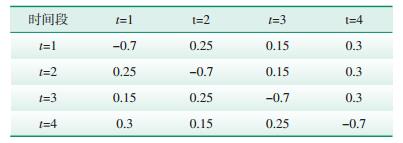
4 算例分析本文以5个电动汽车用户为例,根据价格弹性分为2组,见表 1、表 2。其中,t表示时间段,将1 d分为4个时段。假定各用户的电价响应是确定的,第1组用户对价格相对不敏感,因此εi, t, t′在不同时段的值相对较低;第2组具有较高的价格弹性,并且充电相对灵活。除此之外,5个用户都有相同的电价。弹性矩阵(见表 1、表 2)均设为无损,即弹性系数总和为0,这也符合本文目标函数的目的,即削峰填谷而不是削减负荷。该仿真基于MATLAB完成。
| 表 1 用户组1价格弹性矩阵 |
| 表 2 用户组2价格弹性矩阵 |
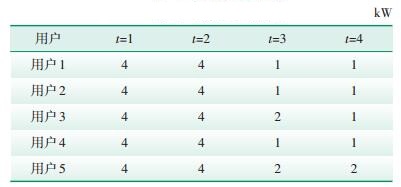
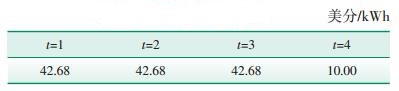
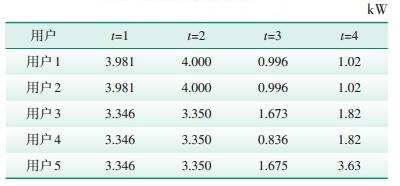
初始电价πt0设为20美分/kWh,其中,10美分表示电能短期边际成本,另外10美分表示传输容量约束,因此,本文电价下限设为边际成本,即10美分/kWh。每一时刻系统传输容量限制见表 3,电价调整前初始充电负荷见表 4。
| 表 3 每一时刻传输容量限制 |
| 表 4 初始负荷需求 |
表 5给出了经过优化算法后的最新电价,表 6给出了优化后充电负荷需求。
| 表 5 各时刻优化后电价 |
| 表 6 优化后充电负荷需求 |
优化后总负荷需求为51.49 kWh,相比初始负荷需求53 kWh下降了2.8%。本文是在仅有5个电动汽车用户条件下的仿真结果,可以判断,在更多电动汽车用户接入的条件下,总负荷将会下降更多。
但是这与本文最初设定的仅“削峰”而不是削减负荷原则有一定偏差,原因在于本文电价弹性矩阵的设定。第一时段的用电负荷仅仅与下一时刻的电价变动有关,而最后时刻的电力需求负荷仅与上一时刻的电价变动有关,也就是说在连续时间段的情况下这种偏差会得到改善。
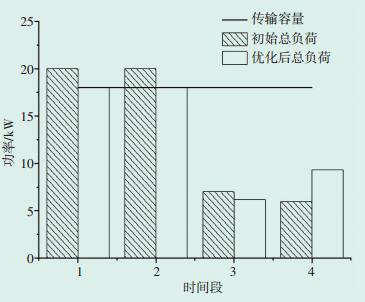
图 6为优化后负荷、初始负荷需求和传输容量的柱状图。可以看出,初始负荷在没有经过电价调整的情况下有越限的情况发生,这是十分不利于电力系统的安全稳定运行的。优化后则将最大充电负荷限制在潮流限制之内。
|
图 6 优化后负荷、初始负荷和传输容量的柱状图 |
由于2组用户有不同的弹性价格,根据表 6可以看出不同的用户对价格的响应情况。用户1相对用户2在电价变动时几乎不调整自己的用电需求,可以说其需求是刚性的。例如,第一时段在相同价格信号条件下,用户1仅仅减少了0.02 kWh的需求,即下降了0.2%;而用户4减少了0.65 kWh的需求。可以预测,在1个区域内有大量电动汽车用户的情况下,通过调查、统计等方式研究用户组对电价的响应系数,可以很好地对用户的用电负荷进行调节,充分发挥优化负荷曲线的能力。
5 结语本文通过建立电动汽车用户行驶行为的概率模型,针对3种不同的充电模式进行蒙特卡罗仿真,模拟了各自的充电负荷曲线,分析了充电负荷对电网安全稳定的影响;同时考虑电动汽车用户对电价的响应,利用价格弹性与需求的关系,建立了以优化负荷曲线为目标的数学模型。最后,本文通过算例证明了该模型在优化电价、削峰填谷中的现实意义,为今后进一步研究消费者对电动汽车电价的响应提供了参考。
| [1] | 吴红斌, 侯小凡, 赵波, 等. 计及可入网电动汽车的微网系统经济调度[J]. 电力系统自动化, 2014(9): 77–84. |
| [2] | 罗卓伟, 胡泽春, 宋永华, 等. 电动汽车充电负荷计算方法[J]. 电力系统自动化, 2011(14): 36–42. |
| [3] | 田立亭, 史双龙, 贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术, 2010(11): 126–130. |
| [4] | 庄怀东, 吴红斌, 刘海涛, 等. 含电动汽车的微网系统多目标经济调度[J]. 电工技术学报, 2014(S1): 365–373. |
| [5] | 项顶, 宋永华, 胡泽春, 等. 电动汽车参与V2G的最优峰谷电价研究[J]. 中国电机工程学报, 2013(31): 15–25. |
| [6] | 邹文, 吴福保, 刘志宏. 实时电价下插电式混合动力汽车智能集中充电策略[J]. 电力系统自动化, 2011(14): 62–67. |
| [7] | Rotering N, Ilic M. Optimal Charge Control of Plug-In Hybrid Electric Vehicles in Deregulated Electricity Markets[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1021–1029. DOI:10.1109/TPWRS.2010.2086083 |
| [8] | Hatziargyriou N, Lopes J A P, Soares F J, et al. Mobile energy resources in grids of electricity:the EU MERGE project[C]//Proceedings of 20102nd European Conference on SmartGrids & E-Mobility. Brussel:Ostbayerisches Technologie-Transfer-Institut e.V. (OTTI)2010:20-21. |
| [9] | 刘文霞, 赵天阳, 邱威, 等. 规模化EV充电与风力/火电发电系统协调运行[J]. 电工技术学报, 2013, 28(5): 49–57. |
| [10] | 胡泽春, 宋永华, 徐智威, 等. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报, 2012, 32(4): 1–10. |
| [11] | 张聪, 许晓慧, 孙海顺, 等. 基于自适应遗传算法的规模化电动汽车智能充电策略研究[J]. 电力系统保护与控制, 2014(14): 19–24. |
| [12] | Schweppe F C, Caramanis M C, Tabors R D, et al. Spot Pricing of Electricity[J]. Kluwer International, 1988, 144(5): 399–405. |
| [13] | 孙衔华, 蒲勇健, 张勇. 我国电动汽车分时电价研究-基于区域性电力市场的网格聚类方法[J]. 价格理论与实践, 2015(11): 156–158. |
| [14] | 魏大钧, 张承慧, 孙波, 等. 基于分时电价的电动汽车充放电多目标优化调度[J]. 电网技术, 2014, 38(11): 2972–2977. |
| [15] | Venkatesan N, Solanki J, Solanki S K. Residential demand response model and impact on voltage profile and losses of an electric distribution network[J]. Applied Energy, 2012, 96(3): 84–91. |
| [16] | Aalami H A, Moghaddam M P, Yousefi G R. Modeling and prioritizing demand response programs in power markets[J]. Electric Power Systems Research, 2010, 80(4): 426–435. DOI:10.1016/j.epsr.2009.10.007 |
| [17] | Gottwalt S, Ketter W, Block C, et al. Demand side management-A simulation of household behavior under variable prices[J]. Energy Policy, 2011, 39(12): 8163–8174. DOI:10.1016/j.enpol.2011.10.016 |
 2017, Vol. 35
2017, Vol. 35