近年来,在我国电力行业中,风电装机容量不断增加.根据2015年中国风电装机容量统计报告,全国(不含台湾地区)新增风电机组16 740台,装机容量为30 753 MW,累计安装风电机组92 981台,装机容量达145 362 MW[1].
风力发电的不可预测性和波动性给电网带来了巨大压力,导致风电场中的弃风现象越来越严重[2],造成大量风资源的浪费.基于风电场大量的历史运行数据,通过编程、建模等技术手段计算限电期间风电场的理论输出功率,具有以下重要意义:有助于提高风电场功率测量数据的质量,间接提高功率预测的精度;有助于科学评估风电场的限电电量,掌握风电场的真实运行情况;有利于调度部门合理制定风电场出力恢复期间的发电计划.
目前,国外特别是风电技术发达国家,由于其灵活的电源结构和联络线支撑能力,几乎不存在限电问题[3].因此,他们对于理论输出功率的计算主要集中在发电能力评估方面.G Giebel等人采用数值流模型对天气预报数据进行修正,并依据风机理论输出功率曲线计算风电场的理论输出功率[4],该方法计算复杂且精度较低.B Smith等人分析了风力涡轮机附近的复杂地形,提出风速测量的精确度是影响功率预测的1个重要因素,但风速计算模型较为复杂[5].姜文玲等人采用机舱风速法,基于风电机组正常运行时段的输出功率与机舱风速计的测量风速建立映射关系,再应用于弃风时段风电场理论输出功率的计算[6],但该方法未指出在确定风速与输出功率之间的映射关系之前,需要对原始测量数据进行预处理,以剔除其中的异常值,提高预测精度.国家电网公司科学研究院的学者提出利用测风塔对实际风速进行测量,根据无弃风条件下的历史数据得到理论输出功率的计算模型[7],该方法需要有完整的调度计划,以便利用无弃风状态下的数据,且该方法是从宏观角度进行分析,计算难以达到精细化.宋颖巍等人从风能利用系数函数出发,对测量的风速进行修正,带入风能转化原理公式获得理论输出功率[8],该方法过于依赖测量风速,计算精度较低.任华等人通过分析风电场的调度运行情况,提出了4种弃风电量的统计方法[9],并进行了对比分析,对弃风统计有一定的参考价值.
本文提出一种基于历史运行数据的风电场理论输出功率计算方法(以下简称新方法).该方法依据风电场的历史运行数据,采用双四分位[10]与聚类相结合的方法剔除限电期间及风机故障时的非正常数据,然后采用Bin[11]和最小二乘法相结合的方法拟合得到单机实际功率曲线,并计算理论输出功率.相比于其他方法,该方法的优势在于:不需要风电场记录完整的调度控制指令;对单台风机建立模型,理论输出功率计算精度较高;具有自适应性,可以实现模型的自动更新.
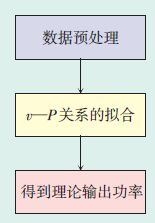
1 新方法介绍新方法的基本思路如下:根据风机类型和实际运行情况,对历史运行数据进行预处理,并利用处理后的数据建立单机风速—功率(v—P)计算模型.理论输出功率的计算步骤如图 1所示.
|
图 1 理论输出功率的计算步骤 |
机组的运行可以划分为4个阶段:当风速低于切入风速时,机组的输出功率为0;当风速介于切入风速和额定风速之间时,机组的输出功率随风速的增大而增大,呈非线性关系,当风速达到额定风速时,输出功率达到机组额定功率;当风速介于额定风速和切出风速之间时,机组的输出功率保持恒定;当风速达到切出风速时,风轮刹车,机组停机.
由于人为操作、设备故障等原因,从风电场采集的数据存在一些问题,需要对其进行预处理,剔除其中的异常数据,并对缺失数据进行填补.首先要将以下3种情况下[12]的数据进行剔除:
(1) 风速未达到切入风速,机组的输出功率为0;
(2) 风速达到切出风速,风轮刹车,机组停机;
(3) 机组发生故障或人为干预造成机组停机.异常数据的分布有堆积型和分散型,通过对比分析,选用双四分位法和聚类法相结合的方法对数据进行处理.双四分位法可剔除常规的分散型异常数据,聚类法可以剔除堆积型异常数据,通过2种方法的结合,可以对风电场中的异常数据进行有效剔除.
双四分位法对风场历史数据中的风速及机组输出功率2组数据分别进行四分位法处理.四分位法是1种统计分析方法,它的基本思想是:将排序后的数据进行分段处理,然后找出数据的有效取值范围,将该范围外的数据看作异常数据并删除.聚类分析法是研究多要素事物分类问题的统计方法,其基本原理是:根据样本数据自身的属性,采用数学方法按照样本数据的相似性指标,定量地确定样本之间的亲疏关系,并按这种亲疏关系程度对样本进行聚类,从而达到将具有相似属性的数据聚为一类,分离出异常数据的目的.本文采用Matlab软件对风电场历史数据进行聚类分析.
1.2 v—P关系的拟合对v—P的拟合采用Bin和最小二乘法相结合的方法.
Bin方法在拟合过程中需要应用所有的数据,由此绘制的曲线平滑,所建立模型误差稳定.该方法首先需要将风速按照大小划分为若干小的区间,这些小区间即风速Bin.为了建模方便,取每1 m/s为1个小Bin,然后将每1个Bin中的风速、功率分别求平均值,得到一个对应点(vi,Pi ),即
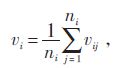
|
(1) |
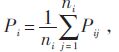
|
(2) |
式中ni—第i个Bin中数据对的数量;
vi—第i个Bin的平均风速;
Pi—第i个Bin的平均功率;
vij—第i个Bin中第j个5 min内的平均风速;
Pij—第i 个Bin中的第j 个5 min内的平均功率.
用1条平滑的曲线将点(vi,Pi )连接起来,即得到Bin方法建模的功率曲线.采用最小二乘法对该曲线进行拟合,得到单机v—P的计算模型为:
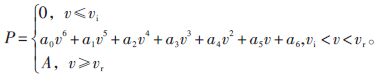
|
(3) |
式中vi—切入风速;
vr—额定风速;
A—风机的理论输出功率最大值.
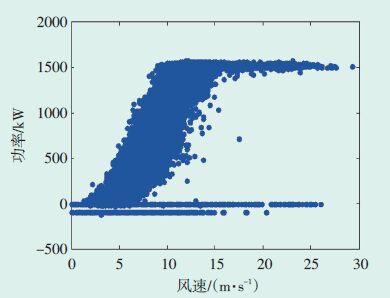
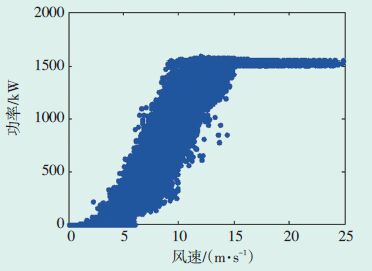
2 实例分析为验证新方法的有效性,以国内北方某风电场2015-01-01—2015-12-31的风速原始数据为例进行算例分析.该风电场装机容量48 MW,包含单机容量1.5 MW的风机32台,采样频率为5 min/点.图 2为1台风机v—P 的原始数据模型,可见其中存在大量异常数据.通过双四分位法及聚类法对原始数据进行预处理,预处理后数据图如图 3所示.
|
图 2 v—P原始数据图 |
|
图 3 预处理后的数据图 |
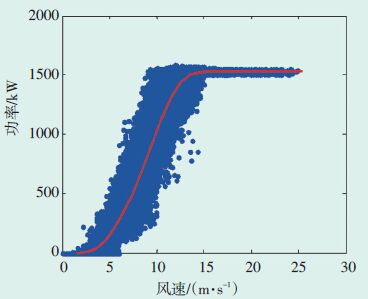
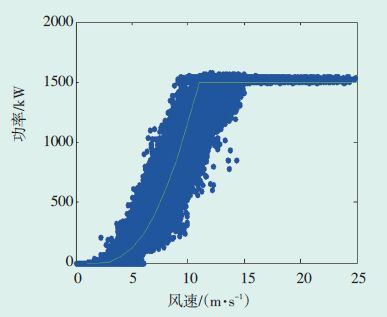
根据新方法,采用Matlab工具箱进行编码,剔除限电期间、风机故障时的非正常数据,然后采用Bin和最小二乘法相结合的方法进行拟合,得到单机v—P 的计算模型.根据计算模型得到某台风机的实际功率拟合结果及出厂功率曲线分别如图 4、图 5所示.
|
图 4 实际功率拟合曲线 |
|
图 5 出厂功率曲线 |
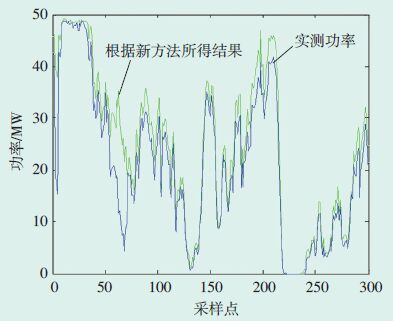
根据新方法所得的实际功率曲线和出厂功率曲线分别对理论输出功率进行计算.以实测风速作为输入数据,计算单机数据中限电期间及风机故障时的非正常数据的理论输出功率,再进行求和得到风电场理论输出功率.为了验证新方法的有效性,分别对2015年1月、5月、9月风电场的理论输出功率进行计算.图 6、图 7、图 8,分别为2015年1月使用新方法得到的理论输出功率计算结果、使用出厂功率曲线得到的理论输出功率计算结果及2种方法计算结果的对比.图 9、图 10、图 11分别为2015年5月使用新方法得到的理论输出功率计算结果、使用出厂功率曲线得到的理论输出功率计算结果以及2种方法计算结果的对比.图 12、图 13、图 14分别为2015年9月使用新方法得到的理论输出功率计算结果、使用出厂功率曲线得到的理论输出功率计算结果以及2种方法计算结果的对比.
|
图 6 采用新方法得到的1月份理论输出功率计算结果 |
|
图 7 采用出厂功率曲线方法得到的1月份理论输出功率计算结果 |
|
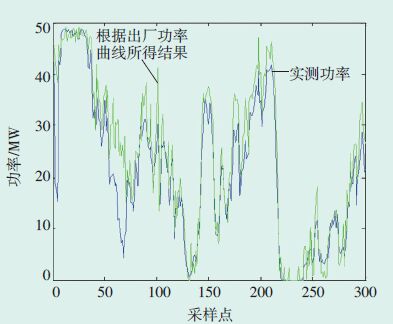
图 8 采用2种方法得到的1月份理论功率计算结果对比 |
|
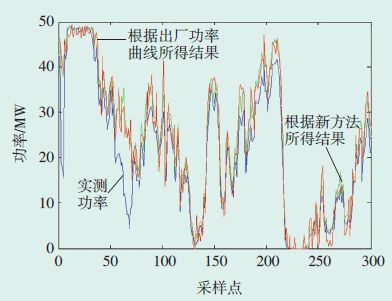
图 9 采用新方法得到的5月份理论输出功率计算结果 |
|
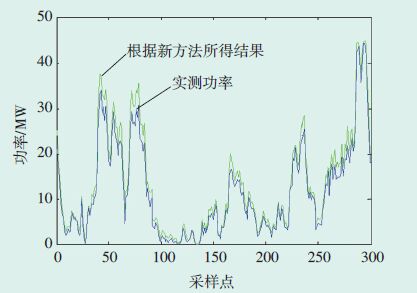
图 10 采用出厂功率曲线方法得到的5月份理论输出功率计算结果 |

|
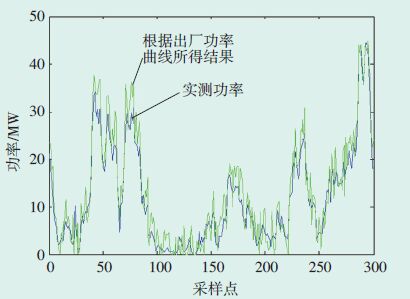
图 11 采用2种方法得到的5月份理论功率计算结果对比 |
|
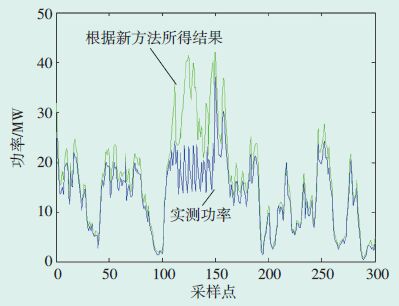
图 12 采用新方法得到的9月份理论输出功率计算结果 |
|
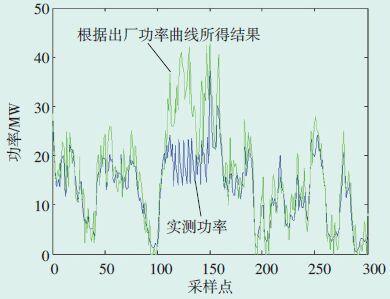
图 13 采用出厂功率曲线方法得到的9月份理论输出功率计算结果 |
|
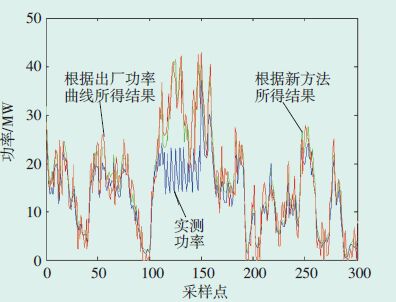
图 14 采用2种方法得到的9月份理论功率计算结果对比 |
本文利用相关性系数反映理论输出功率与实际功率反映之间的相关性,利用偏离度反映理论输出功率的分散程度.相关性系数r 与偏离度d 的计算公式分别如式(4)、(5)所示.
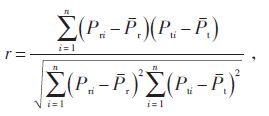
|
(4) |
式中Pr ,Pt—分别为实际功率Pr和理论输出功率Pt的期望值;
n—样本个数;
Pri—第i个样本的实际功率;
Pti—第i个样本的理论输出功率.
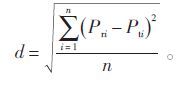
|
(5) |
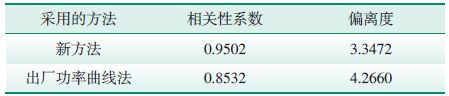
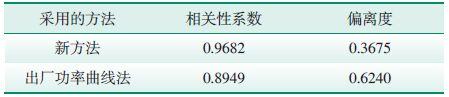
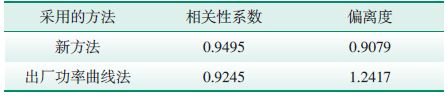
相关性系数、偏离度2个指标的计算结果见表 1、表 2、表 3所示.结合表 1和图 8、表 2和图 11、表 3和图 14可以看出,采用新方法所得结果均优于出厂功率曲线法所得结果,说明新方法能够有效地对风电场理论输出功率进行计算,且计算精度较高.
| 表 1 1月份评价参数计算结果 |
| 表 2 5月份评价参数计算结果 |
| 表 3 9月份评价参数计算结果 |
本文提出的基于历史运行数据的风电场理论输出功率计算方法在应用过程中得到的主要结论如下.
(1) 针对无完整调度指令记录的风电场,采用双四分位法和聚类法相结合的方法可以有效剔除限电期间及风机故障时的非正常数据.
(2) 针对v—P 非线性分布问题,采用Bin和最小二乘法相结合的方法能够有效拟合风机的实际功率曲线,且拟合精度较高.
(3) 将相关性系数和偏离度相结合,能够有效反映风电场理论输出功率计算精度.
(4) 本文提出的方法可为每台风机建立v—P计算模型,该模型具有自适应性,能够获得比出厂功率曲线法精度更高的理论输出功率计算结果,但该方法需要以单机实际功率和风速测量数据为基础.
| [1] | 中国可再生能源学会风能专业委员会. 2015年风电装机容量统计简报[J]. 风能产业 , 2016 (4) :1198–1208. |
| [2] | 祝牧. 多型号LPV模型的识别与两个调度变量[J]. 过程控制学报 , 2012, 22 (7) :1198–1208. |
| [3] | 王铮, 刘纯, 冯双磊, 等. 基于非参数回归的风电场理论功率计算方法[J]. 电网技术 , 2015, 39 (8) :2148–2153. |
| [4] | Giebel G,Badger J,Perez I M,et al.Short-term Forecasting Using Advanced Physical Modelling——the Results of the Anemos Project Results from mesoscale,microscale and CFD modelling[C]//Proceedings of European wind energy Conference.Athens:European Wind Energy Conference and Exhibition,2006. |
| [5] | Smith B,Link H,Randall G,et al.Applicability of Nacelle Anemometer Measurements for Use in Turbine Power Performance Tests:Preprint[C]//Wind Power 2002 Conference.Oregon:AWEA,2002. |
| [6] | 姜文玲, 冯双磊, 孙勇, 等. 基于机舱风速数据的风电场弃风电量计算方法研究[J]. 电网技术 , 2014 (3) :647–652. |
| [7] | 国网电力科学研究院.基于风资源实时监测数据的弃风电量评估方法:中国,CN201110075847.2[P].2011-09-14. |
| [8] | 宋颖巍, 刘岩, 韩震焘, 等. 基于修正风速的风电并网运行弃风电量评估[J]. 电气应用 , 2014 (23) :42–45. |
| [9] | 任华, 姚秀萍, 张新燕, 等. 风电场弃风电量统计方法研究[J]. 华东电力 , 2013 (10) :2148–2152. |
| [10] | 赵永宁, 叶林, 朱倩雯. 风电场弃风异常数据簇的特征及处理方法[J]. 电力系统自动化 , 2014, 38 (21) :39–46. |
| [11] | 黎孟岩, 刘兴杰, 米增强. 风力发电机组功率曲线建模方法研究[J]. 云南电力技术 , 2012, 40 (3) :1–5. |
| [12] | 刘永前, 高小力, 韩爽, 等. 基于修正风速的风电场等效功率特性模型研究[J]. 华北电力大学学报(自然科学版) , 2014 (3) :49–54. |
 2016, Vol. 34
2016, Vol. 34