PID参数优化是一个长期困扰工程技术人员的问题,尽管现在已经有许多用于PID参数整定的方法,但均不够完善,不能使PID控制系统达到理想的控制效果。火电机组主汽温度控制系统控制对象具有纯迟滞、大惯性的特点[1],且调节机构由于受到长期冲刷造成控制对象线性不佳,这些问题给控制系统PID参数的调节造成很大困难。
遗传算法具有控制思路简单、容易实现、应用效果好等优点,近年来在自适应控制、组合优化等许多方面得到了广泛应用[2]。本文对遗传算法控制策略进行研究,利用改进的遗传算法进行PID参数自整定,并采用Matlab仿真软件加以验证,在电厂DCS系统中的应用取得了较好的控制效果。
1 控制策略 1.1 遗传算法介绍 1.1.1 遗传算法公式遗传算法实质上就是求函数极值的优化问题,如公式(1)所示。

遗传算法主要是对公式(1)中适应度函数的确定和解析。确定适应度函数的方法主要有两种:1种是用目标函数的形式给出原始适应度函数,另1种是用目标函数变换的方式来定义标准适应度函数。原始适应函数是求解目标的直接表示,通常采用目标函数作为个体的适应性度量。如在求解极值问题min[f(X)]时,f(X)即为X的原始适应函数。
1.1.2 遗传算法的遗传算子遗传算法的3种遗传算子,即选择算子、交叉算子、变异算子的运算过程如下[3]。
步骤1:初始化,设置进化代数的计数器t=0;设最大进化代数为T;随机生成M个个体作为初始群体N(0)。
步骤2:个体评价,计算群体N(t)中个体的适应度。
步骤3:选择运算,将选择算子作用于当前的群体。
步骤4:交叉运算,将交叉算子作用于当前的群体。
步骤5:变异运算,将变异算子作用于当前的群体。群体N(t)经过选择、交叉、变异运算之后得到下一代群体N(t+1)。
步骤6:若t≤T,则:t=t+1,转到步骤2;若t>T,则以进化过程中得到的具有最优适应度的个体作为最优解输出,计算结束。
1.2 基于遗传算法的PID参数自适应控制策略采用数字PID的控制算法中,遗传算法部分采用二进制编码,采用最常用和最基本的3种遗传算子,即比例选择算子、单点交叉算子和基本位变异算子进行优化操作。
1.2.1 适应度函数的确立根据PID控制器的原理和遗传算法的实现方法,采用二进制编码,以误差绝对积分性能指标作为参数选择的最小目标函数。为防止控制指令过大,在目标函数中加入控制输入的平方项。选用公式(4)计算参数选取的最优指标J[4]:
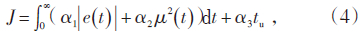
根据目标函数求出个体相对适应度,第n个累积概率等于第n-1个累积概率与第n个个体的相对适应度的和,其中1≤n≤N-1。再利用随机函数产生1个0~1的随机数。若该随机数大于第n-1个累积概率且小于第n个累积概率,则该相对适应度对应的个体被选中。
1.2.3 交叉部分计算根据目标函数求出个体相对适应度,对个体相对适应度进行降序排列,然后计算个体的累积概率。第n个累积概率等于第n-1个累积概率与第n个个体的相对适应度的和,其中1≤n≤N-1。再利用rand函数产生1个0~1的随机数。若这个随机数大于第n-1个累积概率且小于第n个累积概率,则该相对适应度对应的个体被选中。
1.2.4 变异部分计算变异概率Qm控制着变异算子的使用频率,这个概率说明每个染色体中的每1个基因作为变异点的概率为Qm[3]。变异概率的选取以及表达式选择的过程类似交叉操作,从i=1~M重复以下过程:
利用随机函数产生1个0~1的随机数,如果这个随机数小于Qm,则该基因值反向变异,即原来的基因值是1,变异为0;原来的基因值是0,变异为1。如果这个随机数≥Qm,则不进行变异操作。
1.3 算法改进针对遗传算法中存在的迭代次数较多问题,采用1种随代数增加而不断自动调整的交叉概率Pc和变异概率Qm。这样做的目的是:在进化初期,交叉概率较大和变异概率较小有助于加快算法的收敛;而在进化后期,交叉概率较小和变异概率较大有助于防止过早陷入局部最优解。该算法中的交叉概率、变异概率由公式(5)和公式(6)计算[5]:
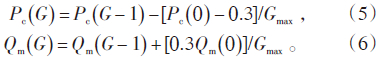
为防止适应度高的个体也有可能被淘汰,在这里采用最优保留策略进行改进,即每代中适应度大于kRaver(k为给定常数,且大于1,Raver为寻优的平均值)的个体不经过遗传操作,直接进入下一代,以便更快地找到最优解。
2 仿真及应用 2.1 Matlab仿真试验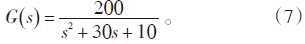
采样时间t=1 ms,指令为阶跃信号。采用改进后的控制算法,用Matlab仿真编程,并进行仿真试验,得到目标函数J的优化过程(见图 1),基于遗传算法优化的参数自适应PID阶跃响应见图 2。由结果可知,目标函数J在第68代时达到其最小值。
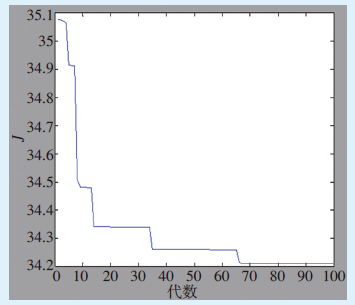 | 图1 目标函数J的优化 |
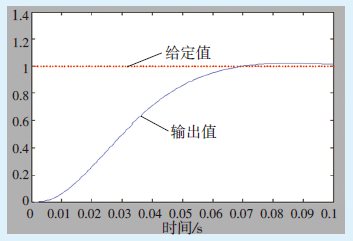 | 图2 基于遗传算法优化的参数自适应PID阶跃响应 |
某火电厂2×300 MW供热机组2号锅炉由哈尔滨锅炉厂有限责任公司制造,型式为亚临界、自然循环、单炉膛四角切圆、一次中间再热、平衡通风、固态排渣汽包锅炉,图 3为主汽温度控制流程图。
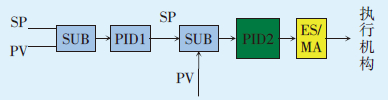 | 图3 主汽温度控制流程图 |
如图 3所示,PID1表示首级控制器(也称主调节器),调节主汽温度;PID2表示次级控制器(也称副调节器),指令为主调节器输出,被调量为过热器前温度。
由于副调节器调节速度较快,具有一定的风险性,因此副调节器由人工调整。主调节器一般采用比例、积分、微分控制,且参数不易调整,因此主调节器可采用基于遗传算法的参数自适应PID控制策略进行参数自动寻优。为不影响电厂的稳定运行,在初步调整确定1个范围后,将适应度函数设置在一定范围内。
2.2.2 试验过程DCS系统采样时间为0.5 s,因该系统响应速度较慢,所以将算法的采样时间定为t=2 s,计算遗传及变异周期设置较长,为15 min。初始值设定比例带PBAND设为2,积分时间INT设置为2 min,微分时间DERIVE为0.7 min,微分增益KD设为1。
遗传算法中,参数PBAND的取值范围为[20, 120],INT和KD的范围都为[1, 10]。选取二进制串来表示每1个参数,编码串长度选为5。再把3个长度为5的二进制串连接起来就组成1个长度为15的二进制字串,该字串为遗传算法可以操作的对象。该项目遗传算法中使用的样本个数为20,终止进化代数为50,交叉概率和变异概率分别为:Pc=0.6,Qm=0.001;最优指标如公式(4),其中权值:α1=1.5,α2=0.01,α3=2.0。
对交叉算子和变异算子进行优化。比较前后2次响应值,如果超调量增加,则直接将积分时间变异(往大跳变);如果系统响应速度变慢,则将比例部分交叉变异(向小的方向转变);如果系统采样值静态偏差变大,则积分时间选择直接往小值变异[8]
2.2.3 试验结果PID参数进行自适应后,进行温度扰动试验。主汽温度给定值变化10 ℃时,主汽温度响应时间为8 min,超调量为0,静态偏差<±1 ℃,主汽温度定值扰动曲线如图 4所示。主蒸汽流量在520~700 t/h变化时,主汽温度偏差<±3 ℃,主汽温度动态跟踪曲线如图 5所示。试验结果表明,该控制系统达到了较好的控制效果。
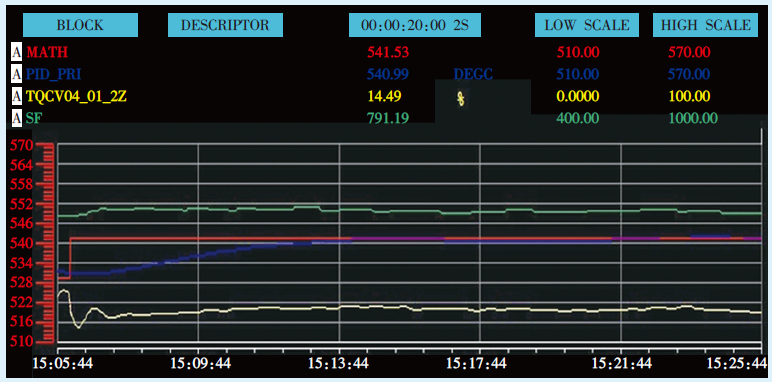 | 图4 主汽温度定值扰动曲线 |
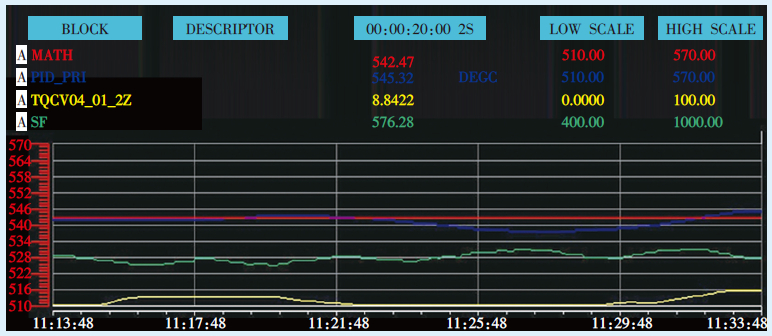 | 图5 主汽温度动态跟踪曲线 |
将遗传算法引入火电厂控制系统中,实现了基于遗传算法的参数自适应PID控制策略在火力发电机组DCS 中的应用,使现场自动控制系统实现了PID参数自适应;并将动态优化引入遗传算法中,提出“改进型遗传算法”的控制策略,优化了控制策略,提高了控制策略的实用性。通过仿真及现场试验,证明该控制策略控制品质良好。该控制策略可用于执行机构磨损严重的控制对象,解决因控制器磨损造成自动控制系统调节品质下降等问题。
| [1] | 张玉铎,王满稼.热工自动控制系统[M].北京:中国水利电力出版社,1985. |
| [2] | 潘是伟.遗传算法在深基坑支护结构优化设计中的应用[D].福州:福州大学,2002. |
| [3] | 周杨.遗传算法在边坡稳定性评价中的应用[D].郑州:郑州大学,2003. |
| [4] | 侯志祥,申群太,李河清.基于改进遗传算法的PID参数整定及其在加热炉中的应用[J].计算机工程,2004,30(6): 165-167. |
| [5] | 郑大忠.线性系统理论[M].北京:清华大学出版社,1990. |
| [6] | 刘景茂.弹用涡扇发动机数学模型建立及控制算法研究[D].西安:西北工业大学,2007. |
| [7] | 薛定宇.反馈控制系统设计与分析—MATLAB语言应用[M].北京:清华大学出版社,2000. |
| [8] | 梁惠冰,孙炳达.现代控制理论基础[M].北京:机械工业出版社,2000. |
 2016, Vol. 34
2016, Vol. 34 
