2. 山东省产品质量检验研究院, 济南 250102;
3. 山东建筑大学, 济南 250101
2. Shandong Institute for Product Quality Inspection, Ji'nan 250102, China;
3. Shandong Jianzhu University, Ji'nan 250101, China
支持式管型母线(以下简称支持管母)是变电站的重要组成部分[1],支持管母系统结构主要包含母线支架、支柱绝缘子、管型母线及固定金具等,这种结构导致了在地震时支持管母系统的固有频率可能与地震主要频率接近,容易发生共振[2, 3, 4]。而支撑管母往往有很多组支架,这些支架通过管母线连接在一起,在地震工况下产生耦合作用,加剧支柱绝缘子的损坏程度。因此,合理选择管母直接关系到变电站的安全运行。
现有的工程规范中关于支持管母的选型和计算日趋完善,但管母在地震工况下的应力强度计算仍未形成完整的计算体系[5]。本文针对实际工程支持管母模型进行管母应力计算公式理论推导及仿真计算,分析其在地震工况下的响应,以便更准确地了解该类系统的抗震能力,为变电站支持管母的选型提供确切的依据。
1 地震作用弯矩计算支持管母由2个或多个支架支撑,结构如图 1所示。
 |
图 1 支持管母结构 |
按照《电力设施抗震设计规范》要求,振型分解反应谱法适合管母地震力计算[6, 7],可分为5个步骤。
(1)形成多质点弹簧体系动力模型,并计算频率和振型。
将管母简化为多质点弹簧体系,即本来分布质量的无限自由度体系可简化为有限自由度的多质点体系。
如果体系有n个自由度,就可计算出n个频率ω1、ω2……ωn及n个振型:

(2)计算所考虑的各频率、振型对应的振型参与系数γ,第j振型参与系数γj为:
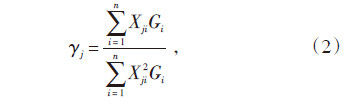
式中 Gi—i质点的重力荷载代表值;
Xji—第j振型i质点的相对位移。
(3)计算所考虑的各频率、振型对应的地震影响系数α,通常α与场地指数和场地特征周期有关。
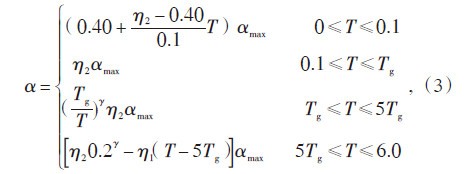
式中 α—地震影响系数;
αmax—地震影响系数最大值;
η1—斜率调整系数;
η2—阻尼调整系数;
Tg—特征周期;
T—结构自振周期;
γ—衰减指数。
(4)计算所考虑的各频率、振型对应的地震作用和地震作用弯矩。
对于n 个自由度的体系,所考虑的每个频率、振型对应着n个地震作用:

式中 Fji—j振型i质点的地震作用标准值;
αj—j振型自振周期的水平地震影响系数;
γj—j振型的参与系数。
确定了所考虑的各个振型的地震作用后,依据该结果计算出弯矩[5]。
(5)计算组合地震作用弯矩。
如果所考虑的各振型的地震作用对应弯矩记为Sj,总的地震作用弯矩S为:

在地震弯矩计算时,可将管母简化为多质点弹簧体系,计算其频率和振型。
将管母四等份分段缩聚简化。四等份分段后每段的质量往该段的两端集中,但集中到2支座处的质量没有位移因此不必考虑,整根管母简化为3个集中质点,这时的动力学简图见图 2。
 |
图 2 管母动力学简图 |

式中 m1、m2、m3—质点1、2、3的质量;
m —单位长度管母质量;
l—管母跨度;
mj—隔离开关静触头(或引下线)的质量。
对于图 2所示的振动体系,可推导出其3个自振频率计算公式:
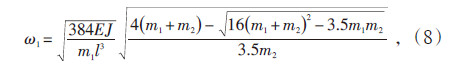

式中 E—弹性模量;
J—截面惯性矩。
对应于这3个自振频率的振型是:

式中 βX1—振型1中质点2的振幅;
βX3—振型3中质点2的振幅。
3 地震工况下支持管母选型计算步骤按上述计算方法进行地震工况下支持管母选型计算,假设支持管母的结构、导体数据如表 1所示。
| 表 1 支持管母的结构、导体数据 |
(1)计算管自重产生的跨中弯矩[5]:

(2)计算隔离开关静触头及金具重力的跨中弯矩:

(3)按前述步骤,根据公式(1)—(15)计算地震工况下各参数。计算结果如表 2所示。
| 表 2 地震工况下各参数计算结果 |
根据计算结果,结合管母缩聚简化模型,可得地震工况下管母的振型,见图 3(m1=m3=7.14 kg,m2=22.14 kg)。
 |
图 3 地震工况下管母振型图 |
(4)假设由风作用产生的跨中弯矩:

(5)合成的跨中弯矩:

(6)由跨中弯矩计算应力:

最后,将上述结算结果与所选管母的最大允许应力[3]相比较:若该计算值小于管母的最大允许应力,说明管母选型满足应力要求;反之,则不满足应力要求。
4 有限元软件仿真分析根据算例提供的数据,采用MIDAS/Gen软件对该支持管母进行有限元分析计算。MIDAS/Gen软件是面向建筑结构分析与设计的通用有限元软件,具有以用户为中心的便捷的输入功能,适用于大型模型的建模、分析及设计。支持管母三维空间建模示意图见图 4所示。
 |
图 4 支持管母有限元模型 |
采用Lanczos算法,得到管母前六阶振型及频率,见图 5所示。
 |
图 5 管母前六阶振型及频率 |
仿真分析与理论推导相对应的模态是竖向模态(模态1、3、5)。但仿真分析中增加了水平向模态(模态2、4、6),这是由于采用了三维空间模型,同时管母本身具有各向对称性。仿真分析结果显示,水平向振型、频率均与竖向振型、频率接近。对比图 3、图 5可以看出,仿真振型与理论计算振型一致。
频率对比结果见表 3所示。可以看出,2种计算方法得出的振型与频率结果相近,证明理论推导公式计算结果精度在工程误差允许范围内。
| 表 3 频率对比结果 |
按第3节(6)中计算结果校核应力,由于W为定值,仅比较合成弯矩。软件分析与理论计算得到的管母最大内力(合成弯矩)对比结果见表 4所示。
| 表 4 管母最大内力对比结果 |
从表 4可以看出,软件分析与理论计算得到的最大弯矩值相近,两者最大误差为4.5%(小于5%)。理论推导公式计算结果精度满足工程需要,可用于支持管母内力计算及分析。
5 结语本文通过理论推导,定量、定性分析了地震工况下的变电站支持管母的应力强度,得出了支持管母模型频率、振型、应力的数学表达式。最后通过有限元软件建模计算,进一步对支持管母系统进行分析,分析结果和理论计算结果吻合,满足工程需要。
| [1] | 蓝增珏,袁达夫.35-500千伏铝管母线配电装置[M].北京:电力工业出版社,1982:12-60. |
| [2] | 谢强,朱瑞元.汶川地震中支持式管型母线破坏机理分析[J].电力建设,2010,31(3):8-12. |
| [3] | 中国电力行业电力规划设计标准化技术委员会.DL/T 5222-2005导体和电器选择设计技术规定[S].北京:中国电力出版社,2005. |
| [4] | 中国电力行业电力规划设计标准化技术委员会.DL/T 5352-2006高压配电装置设计技术规程[S].北京:中国电力出版社,2007. |
| [5] | 弋东方.电力工程电气设计手册(电气一次部分)[M].北京:中国电力出版社,1989:344-347. |
| [6] | 中国电力企业联合会.GB 50260-2013电力设施抗震设计规范[S].北京:中国计划出版社,2013. |
| [7] | 中华人民共和国住房和城乡建设部.GB 50011-2010建筑抗震设计规范[S].北京:中国建筑工业出版社,2010. |
 2016, Vol. 34
2016, Vol. 34 




