为应对全球性的能源和环境危机,世界各国纷纷寻找清洁的可再生替代能源,其中风力发电是当前技术最成熟、应用最广泛的新能源形式。我国风电装机容量连续多年快速增长,目前已居世界首位,但受限于资源与负荷需求的时空分布不均衡,采取了“集中接入、远距离外送”模式。大型风电基地往往位于电网结构较为薄弱的区域,系统安全约束逐渐成为限制风电发展的瓶颈。酒泉、张北风电基地外送能力均受限于送出通道N-1故障后的区域间振荡模式阻尼不足,因此研究风电接入影响对提升电网稳定水平、提高风电接纳能力具有重要意义。
大型风电基地的并网运行会对系统阻尼产生影响。文献[1, 2, 3, 4, 5]建立了可用于小干扰稳定分析的风力发电机组数学模型;文献[6, 7]借鉴同步发电机PSS(电力系统稳定控制器),提出了双馈风电机组附加阻尼控制能取得良好的控制效果,但目前尚未有实际应用报道;文献[8]研究了双馈风电机组不同运行状态和控制参数对阻尼特性的影响,指出双馈风电机组的电压控制环节对阻尼特性有较大影响;文献[9, 10]分别以9节点系统和新英格兰10机39节点系统为算例,从特征值角度研究了不同运行工况及接入位置下风电对系统振荡模式的影响。
本文从双馈风电机组数学模型入手,建立了能反映电网运行特性的典型小系统,采用特征值分析和时域仿真相结合的方法,研究了风电接入对电网区域间振荡模式的影响,并分析主要影响因素。
1 双馈风电机组模型双馈风电机组是当前风电发展的主流机型。在异步电动机的基础上,双馈电动机转子侧通过“背靠背”换流器与电网相连,由PWM换流器向转子提供交流励磁电流。本文采用PSD电力系统分析软件中GE双馈机组模型,该模型包括风速模型、涡轮机及其控制系统模型、双馈电动机和换流器模型、换流器控制系统模型等,其控制结构如图 1所示。采用GE 双馈机组模型的电网线性化方法在文献[1, 2, 3, 4, 5]中有详尽描述,此处不再赘述。
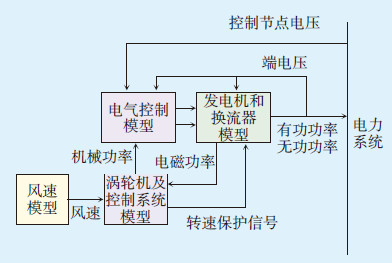 | 图1 双馈风电机组控制结构 |
酒泉风电基地和张北风电基地均位于重要送电通道中段,送/受端机群的区域间振荡是决定输送能力的主导振荡模式。为了仿真分析该地区送/受端振荡模式,本文在PSD电力系统分析软件中建立了三机小系统模型,用于抽象表征该电网结构(如图 2所示),母线B位于中点,受端母线C接无穷大机组,SG为同步机组,DFIG为双馈风电机组。
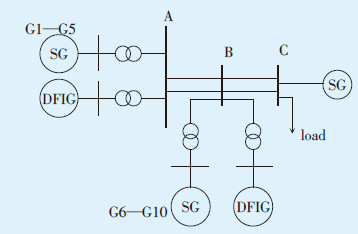 | 图2 三机小系统结构 |
基础方式中母线A和B各接入5台600 MW同步机组;同步机组模型为计及机端电压变化的六阶模型,包含励磁系统、PSS、原动机和调速器模型;风电机组采用GE Energy 1.5 MW机组,额定容量1.5MW,机端电压0.69 kV;风电场通过0.69 kV/35 kV、35kV/220 kV、220 kV/500 kV三级升压变压器升压后接入500 kV电网。
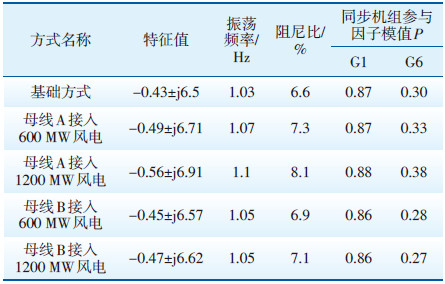
2.2 特征值分析在基础方式中,分别在母线A、B 接入风电机组,同时关停同步机组及调整无功补偿以保持潮流和电压与基础方式一致(启停机组会导致一些局部振荡模式出现或消失,但本文主要讨论系统区域间主导振荡模式,因此局部振荡可忽略不计)。将母线C以外定义为送端系统,主导振荡模式为送端机组相对受端无穷大机组的区域间振荡,特征值分析结果见表 1所示。
| 表 1 不同工况下系统主导振荡模式特征值分析结果 |
由表 1可见,在相同的潮流和电压水平下,风电机组替代火电机组提高了送/受端系统之间的区域振荡模式阻尼比;在接入风电容量相同的条件下,由母线A接入对振荡阻尼的改善作用要明显好于由母线B接入。这是由于风电机组动态响应特性受换流器控制,几乎不参与系统机电振荡模式,因此将同步机组替换为风电机组相当于削弱了振荡源。同时,被替换的同步机组的参与因子模值P 本质上表示机组对振荡模式的特征值灵敏度,P越大,则表明该机组在振荡模式中“贡献”度越高,被替换后的改善效果越明显。由此可知,采用风电机组替代送端火电机组,将改善区域间振荡模式阻尼比,改善程度取决于被替代火电机组在该振荡模式中的参与因子模值。
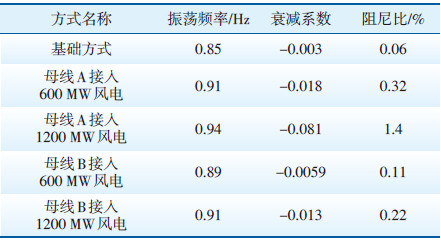
2.3 时域仿真分析按2.2中所述的运行工况(不同风电接入比例与接入位置)进行时域仿真分析,通过设置三相短路故障激起系统振荡,获得风电机组接入对系统振荡的响应特性。图 3为风电机组不同工况下的出力曲线,图 4为剩余一回线路有功功率曲线,表 2为图 4曲线的Prony分析结果。从图 3可以看出,无论风电机组接入母线A 或B,事故后的响应特性一致,均不参与系统振荡,并快速恢复至事故前出力水平。由图 4及表 2可知,风电机组替代同步机组提高了故障后剩余一回线路振荡模式的阻尼水平,特别是替代接入母线A 同步机组的工况改善效果更为明显,与2.2中特征值分析结果完全一致。
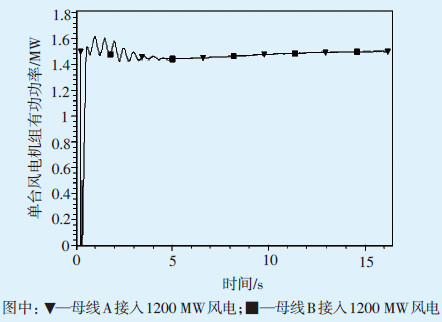 | 图3 故障后单台风电机组有功功率出力曲线 |
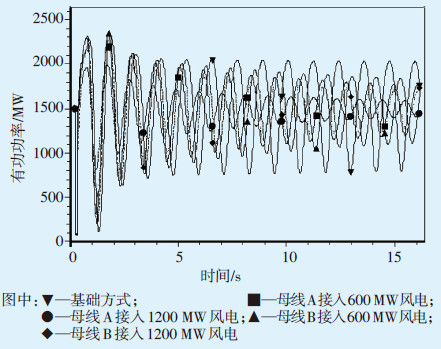 | 图4 N-1故障后剩余一回线路有功功率曲线 |
| 表 2 剩余一回线路有功功率曲线Prony分析结果 |
甘肃河西风电基地为我国目前最大的风电基地,截至2011年年底,风电装机容量5770 MW,升压汇集后接入敦煌、酒泉2个750 kV变电站,其中,酒泉电网内部还有一定容量的火电机组接入。酒泉风电通过西北—新疆联网通道送至西北主网,网架结构如图 5所示。
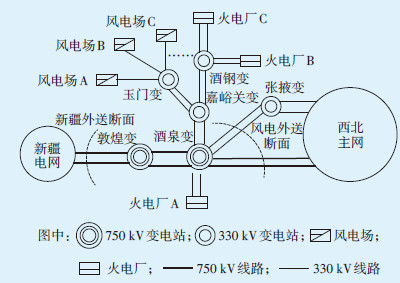 | 图5 酒泉风电基地接入网架结构示意图 |
在PSD仿真环境中建立包含详细风电场模型的西北—新疆联网系统模型,所用同步机组和风电机组模型如2.1章节所述。西北—新疆联网通道为典型的长链送电结构,新疆与西北主网振荡模式为通道输电能力的限制因素,即主导振荡模式。
基础方式中定义泉河双回750 kV线路+酒张双回330 kV线路为风电外送断面,潮流3200 MW,酒泉地区风电上网600 MW,火电1300 MW。在基础方式中增开酒泉电网风电机组、关停火电机组,建立风电满发方式,上网风电800 MW、火电1100MW;同时,建立风电零发方式,关停酒泉电网全部风电机组,火电出力1900 MW。
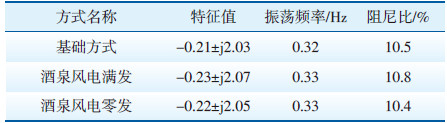
不同方式下西北—新疆联网系统振荡模式特征值分析结果见表 3。由表 3可知,酒泉电网接入风电容量越大,西北—新疆联网系统振荡模式阻尼越强,但变化幅度较小,风电满发与零发方式相比,阻尼比仅相差0.4%。分析该振荡模式可知,接入酒泉地区的火电机组对于西北—新疆联网系统振荡模式参与因子模值均较低,对该振荡模式影响有限,故被风电替换后改善效果不明显。酒泉火电机组参与因子模值见表 4。
| 表 3 不同方式下西北—新疆联网系统振荡模式特征值分析结果 |
| 表 4 酒泉电网火电机组对西北—新疆联网系统振荡模式参与因子模值 |
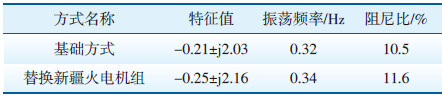
为进一步验证小系统分析结论,在基础方式中选取该振荡模式参与因子模值高的送端新疆火电机组(新通达G1,参与因子模值1;新和丰G1,参与因子模值0.9;新徐矿G1,参与因子模值0.7)合计容量800 MW,在相应位置接入风电机组替代火电机组,系统潮流水平一致,西北—新疆联网系统振荡模式特征值分析结果见表 5所示。
| 表 5 风电机组替换新疆火电机组前后西北—新疆联网系统振荡模式特征值分析结果 |
由表 5可知,与基础方式相比,采用风电机组替代参与因子模值较高的新疆火电机组,西北—新疆联网系统振荡模式阻尼比提高了1.1%,较之替换酒泉火电机组改善程度明显提高。实际结论与小系统完全一致,即风电机组替代送端火电机组,可改善区域间振荡模式阻尼比,改善程度取决于被替代火电机组在该振荡模式中的参与因子模值。
4 结论本文研究风电机组接入替代送端同步机组对系统区域间振荡模式阻尼特性的影响,结论如下:
(1) 由于风电机组响应特性受换流器的控制,风电机组接入电网后,不参与系统区域间振荡模式;
(2) 采用风电机组替代送端同步机组将改善区域间振荡模式阻尼特性,改善程度取决于被替代的同步机组在该振荡模式中的参与因子模值。
| [1] | 尹明,李庚银,周明,等.双馈感应风力发电机组动态模型的分析与比较[J].电力系统自动化,2006,30(13):22-27. |
| [2] | 汤宏,吴俊玲,周双喜.包含风电场电力系统的小干扰稳定分析建模和仿真[J].电网技术,2004,28(1):38-41. |
| [3] | 郝正航,余贻鑫.双馈风电机组机电耦合与轴系稳定的分析与辨识[J].电工技术学报,2011,26(3):134-139. |
| [4] | 刘力卿,余洋,王哲,等.变速恒频双馈风电机组的动态等值方法[J].电力系统及其自动化学报,2012,24(2):63-66. |
| [5] | 高峰,周孝信,朱宁辉,等.直驱式风电机组机电暂态建模及仿真[J].电网技术,2011,35(11):29-33. |
| [6] | 郝正航,余贻鑫,曾沅.改善电力系统阻尼特性的双馈风电机组控制策略[J].电力系统自动化,2011,35(15):25-29. |
| [7] | 王国民,吴政球,彭程,等.双馈电机改善系统阻尼的研究[J].电网技术,2011,35(6):144-148. |
| [8] | 郝正航,余贻鑫.双馈风电场对电力系统阻尼影响的转矩分析[J].电工技术学报,2011,26(5):152-158. |
| [9] | 王忱,石立宝,姚良忠,等.大规模双馈型风电场的小扰动稳定分析[J].中国电机工程学报,2010,30(4):63-70. |
| [10] | 杨黎晖,马西奎.双馈风电机组对电力系统低频振荡特性的影响[J].中国电机工程学报,2011,31(10):19-25. |
 2016, Vol. 34
2016, Vol. 34