自然风具有较强的随机性,风速不但在空间范围内差异较大,历史风速往往也波动较大。风电场的多年平均风速直接影响风电场项目的装机规模、机组选型及发电量等,是风能开发利用的重要指标。风电场项目一般需持续1 a以上的现场测风工作,构建同期测风塔风速(y)与附近气象站风速(x)之间的线性回归方程,通过气象站多年平均风速估算测风塔代表年平均风速。回归分析是风速订正的关键步骤,一般采用最小二乘法原理,使回归残差平方和最小。目前风电场风能资源评估通常采用扇区回归法、直接回归法和简化比值法3种风速订正方法,在样本取用、数据分组、方程简化等过程中,存在多种处置方式,导致预测结果存在较大差异。为明确不同订正方法的适用性,本文结合广东省某风电场工程实例,分别采用3种方法估算回归参数,检验线性回归方程的显著性及标准误差,并对预测结果进行对比评估。
1 通用的风速订正方法 1.1 方法1:扇区回归法扇区回归法由《GB/T 18710—2002 风电场风能资源评估方法》附录A提出[1]。为降低数据随机性影响,该方法要求对相同测风塔风速同时刻的气象站风速做平均处理,处理后的样本按16个风向分别做回归分析,j风向回归方程为:
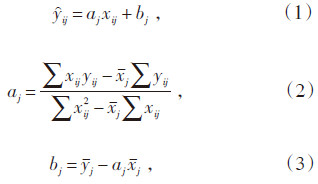
xj 和yj —分别为气象站和测风塔j 风向实测风速平均值;
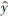 ij —测风塔j风向第i组风速yij的估计值;
ij —测风塔j风向第i组风速yij的估计值;
aj、bj—j风向回归参数。
1.2 方法2:直接回归法直接回归法由《QX/T 74—2007 风电场气象观测及资料审核、订正技术规范》提出[2]。该方法未明确提出对样本进行前处理,可不必按风向分别做回归分析,不分风向的回归方程为:

简化比值法由QX/T 74—2007提出。该方法在直接回归法的基础上发展而来,其前提条件是测风塔与气象站风速在多年序列中处于相同的水平[3],即
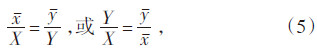

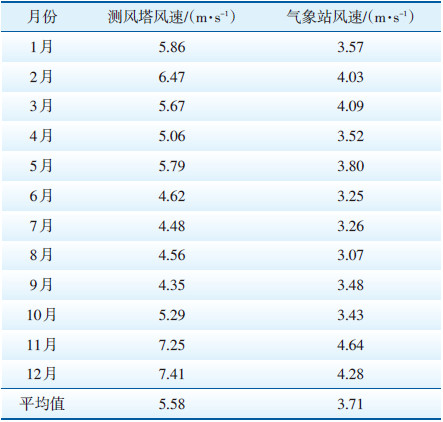
广东省某风电场测风塔与附近气象站相距约35 km,地理环境及气候条件相似性较好。收集测风塔与气象站2个年度内的逐时风速和风向资料,分别按照上述3种方法对第1年度内的风速数据做回归分析,并预测第2年度的风速值。第1年度测风塔与气象站各月份平均风速见表 1,风向分布如图 1所示。
| 表 1 第1年度测风塔与气象站各月平均风速 |
 | 图1 测风塔和气象站同期风向玫瑰图 |
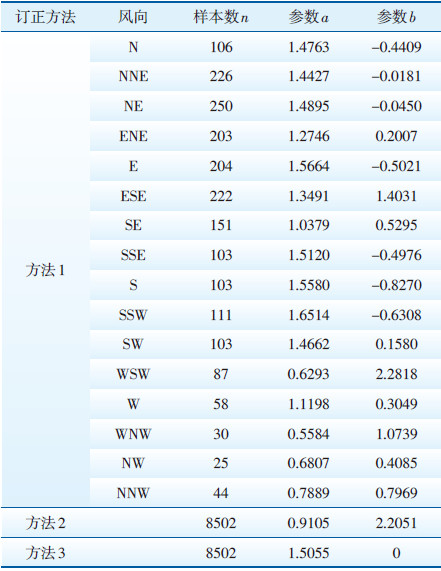
风速订正方法1和方法2采用公式(1)和(4)估算回归参数,满足线性回归及最小二乘法准则;方法3采用公式(6)估计,仅依赖样本平均值,不满足最小二乘法准则。3种风速订正方法的回归参数见表 2。
| 表 2 3种风速订正方法回归参数 |
对于线性回归分析,总偏差平方和TSS、回归平方和ESS、残差平方和RSS关系如下:

可决系数R2和统计量F分别为:
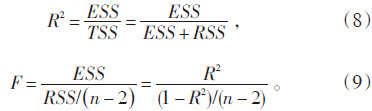
风速订正方法1和方法2采用线性回归方法,适用上述关系;方法3不满足线性回归理论的一般要求,不适用上述关系。
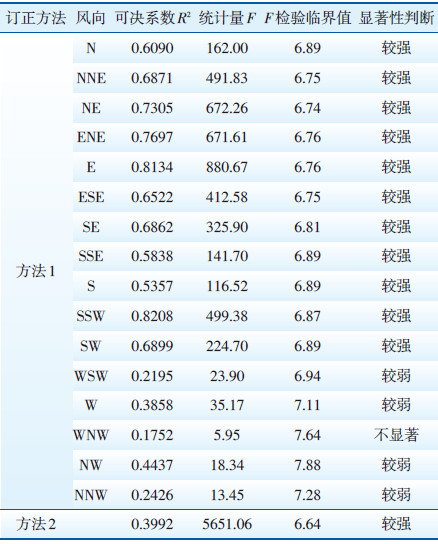
2.3.1 显著性检验采用统计量F 检验线性回归分析的显著性,检验结果见表 3。在0.01 的显著性水平(置信度为0.99)条件下,方法1中WNW风向回归关系不显著,其中N—SW风向显著性较强,其余风向显著性较弱;方法2回归分析具有较强的显著性;方法3的回归显著性无法检验。
| 表 3 线性回归显著性检验结果 |
回归分析的标准误差计算公式如下:
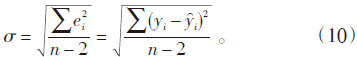
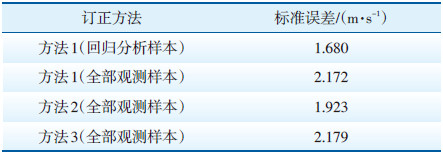
利用公式(10)计算各风速订正方法的标准误差,结果见表 4。从表 4可以看出,方法1的回归分析样本标准误差最小,将回归方程应用于全部观测样本时,标准误差增大;方法2的标准误差较小;方法3在方法2的基础上增加了约束条件,标准误差增大。
| 表 4 不同风速订正方法的标准误差 |
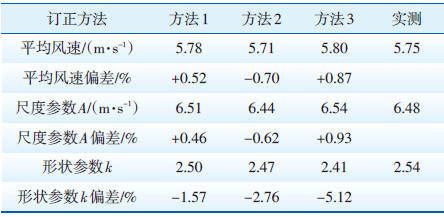
利用测风塔和气象站第1年度的回归分析结果预测测风塔第2年度的平均风速。第2年度气象站年平均风速为3.85 m/s,测风塔实测年平均风速为5.75 m/s。通过测风塔实测风速序列的平均值及标准差统计威布尔分布参数[4],尺度参数A和形状参数k分别为6.48 m/s和2.54。
(1) 方法1中显著性较强的N—SW风向数据采用回归关系订正,其余不具有显著性及显著性较弱的风向不做订正,j风向的风速订正公式为:
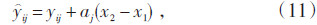
(2) 方法2不分风向做整体订正,公式为:
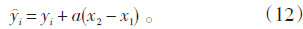
(3) 方法3直接采用比值关系订正,公式为:

使用各订正方法预测测风塔第2年度的风速成果见表 5。从平均风速预测结果看,各方法的预测结果相差较小。其中方法1的预测偏差相对较小,其次是方法2,方法3的偏差相对较大。
| 表 5 第2年度测风塔风速预测成果 |
(1) 方法1采用按风向分组及数据前处理等措施,提高样本的相关性,降低风速随机波动的影响;同时该方法计算量较大,风速前处理降低了回归方程的响应特性。在主导风向显著性水平较高的情况下,可用于风能资源评估及测风塔风速预测。
(2) 方法2使用全部观测样本,严格按照最小二乘法准则,标准误差最小。在统计量F较大、通过显著性检验的情况下,可用于风能资源评估及测风塔风速预测。对于方法1中显著性水平较差的非主风向风速,可尝试采用方法2。
(3) 方法3不依赖于逐时观测样本,适用于快速估算,但误差较大。在基础资料较缺乏或方法1、方法2不可用的情况下,可用作风能资源评估、预测测风塔风速的备用方法。
(4) 实际观测的样本是翔实可靠的数据,但随机波动性较大。方法1采用的前处理措施降低了样本随机性,增强必然相关性,物理意义较强;另一方面,将前处理后的回归方程应用于实际观测样本,增大了标准误差,数学指标减弱。
(5) 在方法1的基础上,对订正结果的后处理措施进行了讨论[5]。后处理措施使结果进一步趋向多年统计规律,同时偏离短期观测规律。
| [1] | 全国能源基础与管理标准化技术委员会新能源和可再生能源分技术委员会.GB/T 18710-2002风电场风能资源评估方法[S].北京:中国标准出版社,2002. |
| [2] | 中国气象局政策法规司.QX/T 74-2007风电场气象观测及资料审核、订正技术规范[S].北京:气象出版社,2007. |
| [3] | 秦鹏,黄浩辉,植石群.东莞风能资源的评估及开发利用[J].广东气象,2011,33(6):47-50. |
| [4] | 国家发展和改革委员会.关于印发《全国风能资源评价技术规定》的通知[R].北京:国家发展和改革委员会,2004. |
| [5] | 杜燕军,冯长青.风电场代表年风速计算方法的分析[J].可再生能源,2010,28(1):105-108. |
 2016, Vol. 34
2016, Vol. 34