2. 太原理工大学, 太原030024
2. Taiyuan University of Technology, Taiyuan 030024, China
同步电机的V形曲线是指以定子电压、输出功率为常数时,定子电流与励磁电流的关系曲线。根据V形曲线,运行人员可以知道定子电压U、输出功率P、定子电流I、功率因数cosφ和励磁电流If之间的关系,例如当励磁电流不变时,负载变化对定子电流和功率因数的影响。因此,研究同步电机的V形曲线对于工程实践有着重要的意义。
通常同步电机的V形曲线采用相量图或解析法进行计算。文献[1]以隐极同步电机为例,依据动态方程的稳态条件获得了V形曲线、稳定极限曲线和当cosφ为定值时I 与If关系的解析表达式。文献[2]对凸极同步电机应用其功角方程和稳定条件,通过求解关于sin2θ和sinθ的三次方程(θ为功率角),得到了V形曲线的解析表达式。但以上方法均没有考虑发电机运行中磁路饱和、磁场畸变等非线性因素的影响[3, 4],导致计算结果与实际情况偏差较大。相比之下有限元法在电机内磁场计算中的应用[5, 6]为V形曲线的研究提供了更加科学的途径。
本文首先介绍了汽轮发电机V形曲线传统的解析计算方法,包括不计与计及磁路饱和(以下简称饱和)2种情况;之后提出了利用有限元法精确计算V形曲线以及利用功角特性曲线族确定静稳极限励磁电流的方法;最后以300 MW汽轮发电机为例,当运行在额定电压时,分别采用有限元法和解析法计算了不同功率下的V形曲线,分析两者之间的差异,并将其应用于发电机的安全运行极限分析,与实测值进行对比,以便为汽轮发电机的运行提供更加准确的数据。
1 传统V形曲线解析计算方法同步电机的V形曲线可以通过电动势相量图间接得到,但该过程需要多步运算,凸极同步电机的求解则更为复杂。文献[1]、[2]分别推导出了隐极同步电机和凸极同步电机在额定电压时的V形曲线和最小电流的求解公式,得到了较为直接的计算方法。
通常发电机制造厂给出汽轮发电机的不饱和电抗xc(同步电抗)和饱和电抗xd(直轴同步电抗)、xq(交轴同步电抗),本文研究了汽轮发电机V形曲线在不计与计及饱和时根据不饱和电抗与饱和电抗进行计算的解析法。
1.1 采用同步电抗不饱和值计算[1]汽轮发电机运行在额定电压时,给定输出功率P,根据d、q 轴动态方程的稳态条件,且近似认为汽轮发电机的xd=xq=xc,可推导出定子电流I 和励磁电流的关系表达式,如式(1)所示(忽略定子电阻的影响)。

给定功率下最小励磁电流Ifmin和对应的定子电流Im由式(2)得到:

由于汽轮发电机转子存在大齿和小齿的区别,不同运行条件下d、q 轴具有不同的饱和特性,因此汽轮发电机计及饱和时,考虑到凸极效应,可将其当作凸极同步电机来分析。为了与有限元法的计算结果一致,本文取空载电势E0=xadIf (xad为直轴电枢反应电抗),对文献[2]中的方法进行了改进。
已知定子电压、有功功率和励磁电流时,若要得到定子电流,首先由式(3)求出功率角θ:


将式(3)所得功率角代入式(4),求出此时的定子电流:

同理,若要得到最小励磁电流和对应的定子电流,首先由式(5)求出稳定极限功角θmax,然后代入式(6)计算:

同步电机运行时受到磁路饱和、磁场畸变等多种非线性因素的影响,电抗会随着运行条件的变化而变化[7, 8]。有限元法可以计及以上因素的影响,其计算励磁电流的准确性已在文献[9]中得到了验证,因此本文采用文献[7]所述的有限元建模方法,将有限元法应用于V形曲线的计算。
2.1 静稳极限励磁电流的确定方法根据利用有限元法得到的功角特性曲线族来确定最小励磁电流Ifmin,具体步骤如下:
(1) 给出1组励磁电流,计算出额定电压时的功角特性曲线族;
(2) 给定有功功率,根据该功率做1条平行于横坐标的虚线,继而确定最小励磁电流的范围;
(3) 对步骤(2)所得励磁电流范围的端点值进行二分,分别求出对应的最大功率,由此缩小励磁电流的范围;
(4) 进一步对励磁电流二分,直到求得某一励磁电流对应的最大功率等于给定的有功功率,该励磁电流即为所求值。
以发电机P=0.85为例,If分别取值为IfN、0.8IfN、0.6IfN、0.4IfN和0.2IfN,其中,IfN为额定励磁电流,得到的功角特性曲线族如图 1中实线所示。由P=0.85做1 条水平虚线,可以看出对应的Ifmin 在0.4IfN~0.6IfN。
 | 图 1 功角特性曲线族 |
对励磁电流进行二分,求得0.4IfN、0.5IfN和0.6IfN对应的最大功率分别为0.6279、0.7751、0.9222,因此Ifmin的范围缩小为0.5IfN~0.6IfN。继续对励磁电流进行二分,最终得到Ifmin=0.5509IfN。
2.2 V形曲线有限元法精确计算流程利用有限元法计算V形曲线时,给定定子电压和有功功率,首先确定该功率下的最小励磁电流和对应的定子电流;然后增大励磁电流,采用牛拉法求解定子电流[10, 11];继续增大励磁电流,直到求得足够的运行点或电流超出限定值。图 2给出了同步电机V形曲线有限元法计算的流程。
 | 图 2 同步电机V形曲线有限元计算流程图 |
当已知U、P、If时,首先由式(1)和式(7)分别给定I和λ的初始值,对应的电动势相量图如图 3所示。

 | 图 3 汽轮发电机的电动势相量图 |
通过磁场计算得到定子电压和有功功率,分别记为Ucal、Pcal,以及相对于给定值U、P 的误差ΔU、ΔP,如果满足式(8)所示的收敛条件,则认为I 和λ满足要求,否则应对I 和λ进行迭代修正,直到满足收敛条件。

以300 MW汽轮发电机为例,分别采用解析法和有限元法对不计与计及饱和时的V形曲线进行计算。发电机参数见表 1所示。
| 表 1 300 MW汽轮发电机参数 |
发电机在额定电压下运行,采用不同方法计算满载与轻载的V形曲线如图 4所示。可以看出不计饱和时采用解析法与有限元法计算的结果十分接近,计及饱和后采用解析法与有限元法计算的V形曲线均向右偏移,且采用有限元法计算的曲线偏移较大,尤其在额定励磁电流附近差异明显。迟相运行时,相同定子电流下采用有限元法计算的励磁电流较大,且功率越低差异越大。
为进一步研究V形曲线解析法与有限元法之间的差异及原因,图 5给出了与图 4a计及饱和时采用解析法与有限元法计算的V形曲线对应的功角θ、气隙电势Eδ、内功率因数角φ、合成电流IΣ随励磁电流的变化曲线。
 | 图 4 采用不同方法计算的V形曲线 |
由图 4a和图 5可以看出,在励磁电流相同的情况下,用有限元法计算的定子电流、功角、气隙电势和内功率因数角比用解析法计算的结果偏小,且φ的差值保持在10°左右。
 | 图 5 计及饱和时的功角、气隙电势、内功率因数角、合成电流变化曲线 |
图 6给出了当励磁电流和定子电流大小相同时,不同φ值对应的合成电流求解相量图。当φ减小时,Id减小,Iq增大,由式(9)可知IΣ将增大,因此采用有限元法计算的合成电流大于采用解析法计算的值。
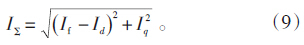
 | 图 6 合成电流的求解相量图 |
汽轮发电机复杂的非线性特性主要是受磁路饱和与磁场畸变2个因素的影响[5]。功角相同时,励磁电流不同导致转子漏磁场不同,影响转子铁心的饱和,而功角较大时磁场畸变导致主磁路的等效气隙长度增加,均会影响合成电流产生气隙电势的大小。
发电机迟相运行时,功角基本在50°以下,磁场畸变不明显,而气隙电势(标幺值)大于1,此时非线性特性主要受铁心饱和的影响。因此,随着励磁电流的增大,气隙电势与合成电流增大,且采用解析法与有限元法计算结果的相对误差增大。
发电机进相运行时,虽然定子电流的差异较小,但其他电气量仍存在较大差异,如功角最大可差10°,合成电流相差24.48%。在静稳定极限附近,功角较大,气隙电势较小,此时非线性特性主要受磁场畸变的影响。以图 4a中有限元法的a、b 两点为例,对应的磁场分布图如图 7所示,a 点的励磁电流和气隙电势小于b 点的,但功角的增大导致磁场畸变程度增强,磁力线斜穿气隙和定转子槽,等效气隙长度增加,导致合成电流增大。解析法不能考虑磁场畸变的影响,所以合成电流仍然随励磁电流的减小而减小,两者相对误差增大。
 | 图 7 a、b两点的磁场分布图 |
综上所述,有限元法可以较好地考虑磁路饱和与磁场畸变等非线性因素的影响。
3.3 V形曲线在安全运行极限中的应用 3.3.1 发电机正常运行条件的限制要求发电机的正常运行条件由安全运行极限图(又称P—Q 容量图)进行限制,具体包括以下4个方面的极限:
(1) 定子发热极限,I≤IN,其中,IN为额定电流;
(2) 转子发热极限,If≤IfN,其中,IfN为额定励磁电流;
(3) 原动机输出功率极限,P≤PN,其中,PN为额定有功功率;
(4) 静态稳定运行极限,If≥Ifmin,其中,Ifmin为最小励磁电流。
结合图 4可以看出,以上极限均能由发电机的V形曲线得到。
3.3.2 进相运行时的最小励磁电流分别采用解析法和有限元法计算的发电机额定电压、不同有功功率对应的最小励磁电流及计算结果相对误差(以有限元法为基准)如表 2所示。
由表 2可以看出,无论是否计及饱和,采用有限元法计算的最小励磁电流小于采用解析法计算的值,说明采用解析法偏于保守,结果没有达到发电机实际的静稳极限。相对误差随有功功率的减小而增大,计及饱和后差异更大,当功率为0.2PN时不计饱和两者的相对误差为7.02%,计及饱和后相对误差已超过40%。
| 表 2 最小励磁电流Ifmin(p.u.) |
从发电机的V形曲线可知,随着有功功率的减小,相同励磁电流所对应的定子电流减小。因此,发电机迟相运行时的安全运行极限由额定励磁电流决定,不同有功功率对应不同的定子电流极限值。
表 3给出了发电机运行在额定电压、不同有功功率的情况下,分别采用解析法和有限元法计算的定子极限电流及相对误差,可以看出,采用有限元法比解析法计算的值偏小,说明采用解析法偏于保守。随着功率的减小,两者的相对误差增大,计及饱和时误差均超过5%。
| 表 3 定子极限电流Imax(p.u.) |
表 4为某电厂300 MW汽轮发电机不同运行条件下,计及饱和时分别采用解析法、有限元法计算的励磁电流与实测值对比结果。可以看出,采用有限元法求得的励磁电流与实测值更为接近,且误差均在5%以下,而采用解析法计算结果的误差偏大,由此验证了应用有限元法计算V形曲线更加精确。
| 表 4 300 MW汽轮发电机If实测数据与计算数据对比 |
本文首先介绍了采用不饱和电抗与饱和电抗计算汽轮发电机V形曲线的解析法,之后提出了基于有限元法的精确计算方法,根据利用有限元法计算的功角特性曲线族确定静稳极限励磁电流,通过对比采用有限元法和解析法计算的V形曲线和极限电流,得到以下结论:
(1) 发电机不计饱和时,用有限元法与解析法计算的V形曲线差异较小,极限电流基本一致;
(2) 发电机计及饱和时,用有限元法与解析法计算的V形曲线均比不计饱和时计算的曲线向右偏移,且采用有限元法计算的曲线偏移较大,可以较好地考虑到各种非线性因素的影响;
(3) 将采用有限元法与解析法计算的V形曲线应用于安全运行极限时,用有限元法计算的进相最小励磁电流及迟相定子极限电流均较小,采用解析法则偏于保守;经与实测值对比,验证了采用有限元法计算结果较为精确。
| [1] | 高仕红.基于动态方程的同步电机V形曲线解析研究[J].湖南民族学院学报(自然科学版),2009,27(4):423-426, 457. |
| [2] | 李时东,李建钊.凸极同步电机V形曲线的解析计算[J].中国电机工程学报,2008,28(18):110-113. |
| [3] | 罗应立,张新丽,康锦萍,等.汽轮发电机非线性特征的机理及其与运行条件的关系[J].中国电机工程学报,2008, 28(17):144-150. |
| [4] | 康锦萍,刘晓芳,罗应立,等.汽轮发电机磁路饱和与磁场畸变共同作用对运行的影响[J].中国电机工程学报, 2010,30(36):41-45. |
| [5] | 张月莉.大型同步发电机稳态磁场非线性特性及运行特性的计算研究[D].北京:华北电力大学,2004. |
| [6] | 陈增芬.考虑饱和时1000 MW水轮发电机运行特性分析[D].哈尔滨:哈尔滨理工大学,2010. |
| [7] | 赵凌志.计及饱和时汽轮发电机运行特性的计算研究及有限元软件设计[D].北京:华北电力大学,2002. |
| [8] | 周济.同步发电机不同运行条件下多因素饱和效应的研究[D].北京:华北电力大学,2001. |
| [9] | 刘晓芳,康锦萍,罗应立,等.汽轮发电机在饱和与磁场畸变时负载励磁电流计算的新方法[J].电机与控制学报, 2010,14(8):7-12. |
| [10] | 李志强,胡笳,祝丽芳,等.同步发电机有限元磁场计算中端点量迭代的改进算法[J].电工技术学报,2008,23 (12):35-41. |
| [11] | 晁晖,李志强,罗应立,等.同步电机场路耦合端点量迭代新算法[J].中国电机工程学报,2009,29(30):63-69. |
 2015, Vol. 33
2015, Vol. 33 




