2015, Vol. 33 
2. 上海电力学院, 上海200090
2. Shanghai University of Electric Power, Shanghai 200090, China
利用系统辨识的基础理论来实现数学模型辨识的方法已经比较成熟，但目前很少有采用现场生产运行数据来获取火电厂协调控制系统模型的研究成果[1, 2]。本文通过对现场生产运行数据进行有效信息的提取和处理，采用基于最小二乘法的辨识拟合，获取了二输入和二输出协调控制被控对象的数学模型，并通过仿真验证，证实模型逼近实际生产运行数据，且有效地描述了火电机组电功率和主汽压力的耦合特性。
1 系统辨识模型现场运行数据的获取火电厂机组级协调控制系统本质上是1个存在强关联的多变量控制对象，经适当假设，可以将其看作具有2个控制输入量（燃料量指令μB，汽轮机调节阀开度μT）和2个被控输出量（机组输出功率PE，主汽压力pt）的对象[3, 4]。机组控制输入量和被控输出量之间的耦合特性可以表示为：μB的改变既影响pt，又影响PE；同样，μT的改变也同时影响pt和PE，具体耦合结构如图 1所示。
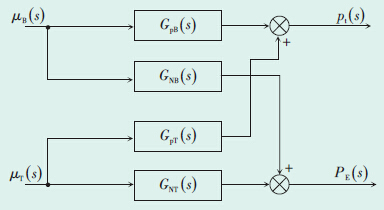 | 图 1 机组输出功率汽压耦合结构 |
同时，输出电功率和主汽压力的耦合特性可以用1组二输入二输出的传递函数矩阵方程来表达[5]，其传递函数矩阵表达式如下：
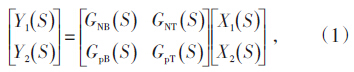
由于系统的耦合动态特性必然表现于输入μ = [μB μT]T 和输出 y = [PE pt]T 数据中，因此可以利用由试验测试法得到的输入量μ = [μB μT]T 、输出量y = [PE pt]T 数据进行辨识来建立系统耦合特性的数学模型。本次试验测试基于300 MW火电机组新华XDPS集散控制系统操作员站平台，分别对控制输入量μB、μT进行阶跃扰动测试，并在操作员站利用趋势图记录采集测试点参数历史数据（见图 2、图 3）。
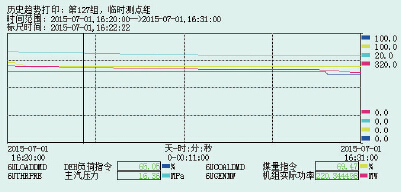 | 图 2 操作员站趋势图记录 |
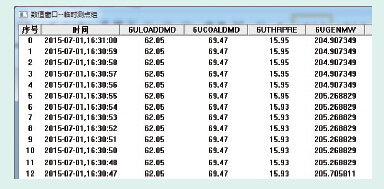 | 图 3 测试点数据记录 |
对所需的现场生产运行数据按以下方法、步骤提取：
（1） 置引风控制、蒸汽温度控制、燃料控制、风量控制和给水控制为自动控制方式[6]。
（2） 进行锅炉主控（BM）指令μB扰动下的机组电功率和主汽压力耦合特性测试试验。
（3） 进行汽轮机调节阀开度μT扰动下的机组电功率和主汽压力耦合特性测试试验。
通过以上步骤，可以提取控制输入量燃料量指令μB，调节阀开度μT和被控输出量电功率PE，主汽压力pt的试验测试数据。提取的相关现场生产运行数据变化曲线如图 4和图 5所示。
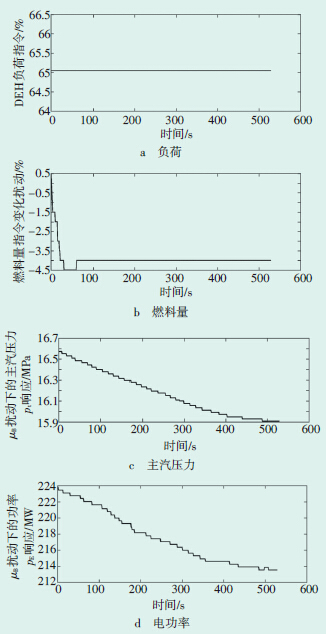 | 图 4 燃料量扰动试验各参数变化曲线 |
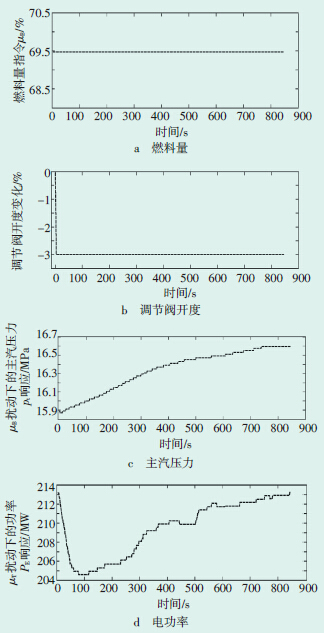 | 图 5 汽轮机调节阀扰动试验各参数变化曲线 |
由图 4可见，当保持汽轮机调节阀开度μT不变，而燃料量指令μB减少时，锅炉蒸发受热面的吸热量减少，主汽压力pt逐渐降低，进入汽轮机的蒸汽流量也随之减少，进而使汽轮机输出电功率降低，因此PE也逐渐降低。当燃料量指令达到新的平衡，主汽压力和电功率也趋于1个新的稳态值。
由图 5可见，当保持燃料量指令μB不变，而μT阶跃减少后，进入汽轮机的蒸汽流量刚开始立即减少，同时主汽压力pt立即增加。由于μB保持不变，所以蒸发量也不变，因此蒸汽流量的减少只是暂时的，最终蒸汽流量仍恢复到与燃烧率相适应的扰动前的数值，主汽压力pt也逐渐趋于1个新的稳态值。
2 基于最小二乘法的模型系统辨识最小二乘法从误差拟合角度对模型进行系统辨识，因其原理简单、易于实现而得到极为广泛应用[7]。为获得电功率和主汽压力耦合特性的传递函数模型，本文采用基于自回归遍历模型（ARX）的最小二乘法进行模型辨识。
根据试验测试获取的控制输入量和被控输出量输出数据，采用最小二乘法在某种准则意义下通过辨识模型
与原系统过程进行最小误差拟合，确定1个与所测系统等价的数学模型[8]，基本原理如图 6所示。
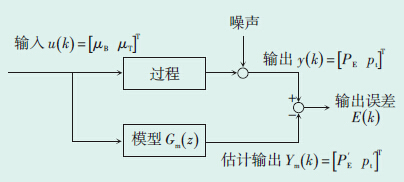 | 图 6 系统辨识原理图 |
假设已经获得在t1，t2，…，tn 时刻对输入μ(k) = [μB μT]T 及输出 y(k) = [PE pt]T 的离散时间观测值序列，并且用Y(k)及U(k)（k=1，2，…，m）来表示输入、输出观测数据，则可以通过输出误差E(k)并利用数据序列极小化下列准则函数式：
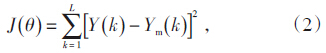
当J（θ）取极小值时，得到模型Gm(z)。其中，θ代表模型参数集，即Ym=UT(k)θ。
3 辨识模型及仿真采用最小二乘法通过Matlab根据试验测试所获取的输入、输出现场运行数据，分别对燃料量指令μB阶跃扰动下的输出电功率PE，主汽压力pt和调节阀开度μT阶跃扰动下的输出电功率PE，主汽压力pt的耦合特性进行系统辨识[10]。
辨识的模型是基于上述试验测试数据曲线，燃料量指令和汽轮机调节阀开度指令同实际机组的指令相对应[11]，机组负荷220 MW、压力16.6 MPa工况点附近进行的燃料量指令扰动试验。
3.1 GNB(z)和GpB(z)辨识仿真汽轮机调节阀开度μT=65.05%，燃料量指令μB由73.47%变化到69.47%，采样周期为1 s，所得到的GNB(z)、GpB(z)辨识仿真结果分别见图 7、图 8。
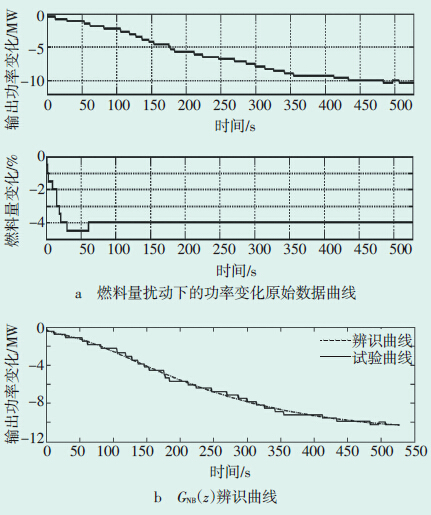 | 图 7 GNB(z)辨识仿真结果 |
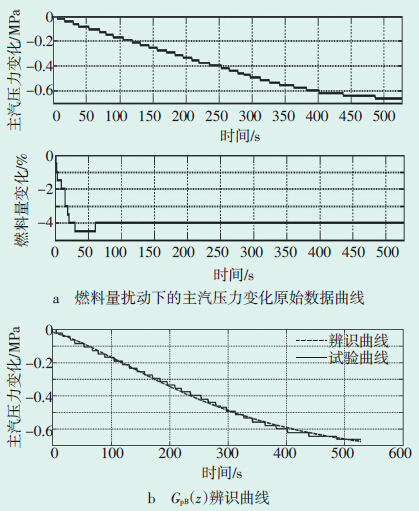 | 图 8 GpB(z)辨识仿真结果 |
由图 7b可见，辨识所得的传递函数模型与试验测试的功率变化曲线能够很好地拟合，燃料量扰动下的输出电功率动态特性模型表达式如公式（3）：
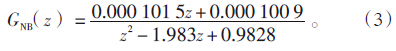
由图 8b可见，辨识所得的传递函数模型与试验测试的变化曲线能够很好地拟合，燃料量扰动下的蒸汽压力动态特性模型表达式如公式（4）：
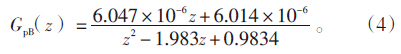
同样，在机组负荷213 MW、压力16 MPa工况点附近进行了汽轮机调节阀开度扰动试验。燃料量指令μB=69.47%，汽轮机调节阀开度由65.05%变化到62.05%，采样周期为1 s，得到GNT(z)和GpT(z)辨识仿真结果。分析仿真结果可见，本文对输出电功率变化曲线进行的辨识拟合与试验测试变化曲线拟合较好，由此得到汽轮机调节阀开度扰动下的电功率变化动态特性模型表达式如公式（5）；燃料量扰动下的主汽压力动态特性模型表达式如公式（6）：
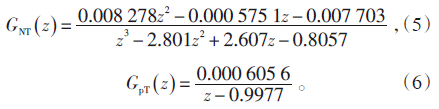
最终可以得到代表输出电功率和主蒸汽压力的耦合特性的系统辨识模型组，见公式（7）：
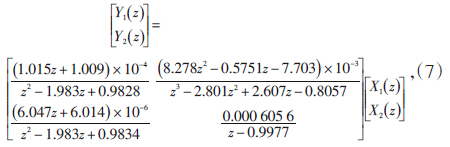
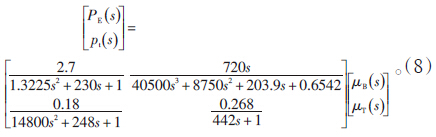
根据300 MW火电机组实际生产运行数据，采用基于最小二乘法的系统辨识方法，对单元机组输出电功率和主汽压力的耦合特性进行辨识，得到了机组在燃料量扰动、汽轮机调节阀开度扰动下的输出功率和主汽压力耦合特性模型，能够很好地拟合原始数据曲线，辨识结果良好。本次辨识得到的模型对进一步开展火电厂协调控制系统解耦控制的研究工作提供了参考模型，另外，现场运行数据的辨识方法对火电厂其他动态特性模型的获取也有一定的借鉴意义。
| [1] | 冯昌,段秋刚,谷大丰.基于模型解耦的协调控制系统研究[J].山西电力,2013(4):54-56. |
| [2] | 林金星,沈炯,李益国.单元机组协调系统的多模型自适应解耦控制[J].东南大学学报(自然科学版),2008,38(3):413-418. |
| [3] | 陈岚峰,张亚琴,程立英,等.基于数据的MATLAB系统辨识工具箱模型识别[J].沈阳师范大学学报(自然科学版),2013,31(4):527-530. |
| [4] | 王建国,孙灵芳,张利辉.电厂热工过程自动控制[M].北京:中国电力出版社,2009. |
| [5] | 江建锋,潘维加.300 MW单元机组机炉协调控制系统的仿真研究[J].长沙理工大学学报(自然科学版),2005,2(1):49-55. |
| [6] | 李鹏波,胡德文,张记阳,等.系统辨识[M].北京:中国水利水电出版社,2010. |
| [7] | 侯媛彬.系统辨识及其MATLAB仿真[M].北京:科学出版社,2004. |
| [8] | 石贤良,吴成富.基于MATLAB的最小二乘法参数辨识与仿真[J].微处理机,2006,26(6):44-46. |
| [9] | 张满良.300 MW火电机组系统辨识模型及仿真分析[D].北京:华北电力大学,2010:5-15. |
| [10] | 任贵杰.单元机组协调控制系统的建模与控制优化研究[D].北京:北京交通大学,2011. |