对于新安装、大修或换油后的变压器,需要进行充电冲击试验,以检验变压器的绝缘特性、机械特性或差动保护躲避励磁涌流的能力。变压器充电保护定值整定计算时,首先需要考虑的就是被充变压器励磁涌流可能达到的最大值及其衰减趋势。但对于不同电压等级、容量及励磁特性的变压器,保护整定人员很难明确掌握励磁涌流与时间的具体关系,给充电保护整定计算带来了困难。本文通过对励磁涌流产生的机理,以及变压器空载充电时励磁涌流的最大值与衰减趋势进行仿真分析,为变压器充电保护定值整定计算提供理论依据。
1 励磁涌流的影响因素 1.1 变压器铁心磁通变压器充电时,既要保证充电保护定值能够躲过励磁涌流,又需保证变压器故障时保护具有足够灵敏度,能够及时切除故障[1]。但由于系统和变压器阻抗的原因,计算出的满足灵敏度要求的定值可能会比励磁涌流的幅值小很多,这就需要为相应的保护定值增加1个时限,保证在此时限内定值能够可靠躲过励磁涌流的峰值。
设系统电压U 为正弦波,U=Umsin(ωt+α),其中,Um为合闸电压幅值,V;ω为合闸角频率,ω=314 rad/s;α为合闸角,(°)。考虑变压器合闸回路电阻、变压器绕组的电阻和漏感带来的时间常数T 的影响,空投变压器铁心磁通Φ与外加电压、合闸角及剩余磁通的时间关系如公式(1)[2]:
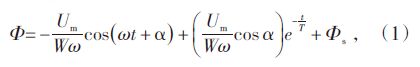
T—时间常数。T=L/R,L 为绕组电感,H;R 为绕组电阻,Ω;
t—时间,s;
Φs—剩余磁通,Wb。
因铁心中强迫磁通的幅值Φm=Um/Wω,则公式(1)可改写为公式(2):
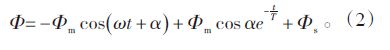
公式(2)中第1项为磁通的强迫分量;第2项为磁通的自由分量,随时间而衰减。如果在电压瞬时值为0时空投变压器,合闸角α=0°,在忽略变压器及合闸回路电阻时,时间常数T 为无穷大,磁通中的自由分量不衰减;当Φs的方向与合闸后Φm相同时,变压器铁心磁通的最大值可达到Φ=2Φm+Φs[3, 4]。
根据变压器原理,变压器充电侧电动势Em与磁通Φ的关系见公式(3)[3]:
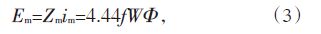
Zm—变压器与系统电源间的联系阻抗,Ω。
1.2 励磁涌流的影响因素分析根据公式(2)、公式(3)可知,变压器励磁涌流与铁心中磁通的幅值有关,磁通越大、铁心越饱和,则励磁涌流越大。由此可见,励磁涌流幅值及衰减的影响因素与磁通相同。对于电网中的充电变压器来说,合闸角频率与匝数是不可随意改变的,所以根据公式(1),影响励磁涌流幅值的因素有合闸电压、合闸角、剩余磁通;其衰减速度与时间常数T有关,T越大,励磁涌流衰减越慢[3]。
1.2.1 合闸电压合闸前,电源电压越高,Φm 越大,励磁涌流越大。
1.2.2 合闸角当合闸角α=0°时,即电压瞬时值为0 V时合闸,磁通强迫分量-Φmcos(ωt +α)的幅值达到最大值-Φm,自由分量Φmcosα也达到最大值Φm,这样在半个周期后,铁心中的磁通达到最大值Φ=2Φm+Φs,此时励磁涌流达到最大值。
在α=90°时,也就是在电压瞬时值为最大时合闸,磁通的强迫分量与自由分量都为0,磁通只剩下剩余磁通Φs,此条件下,铁心中的磁通的最大值Φ=Φm+Φs;最小值Φ=-Φm+Φs,此时励磁涌流达到最小值。
1.2.3 剩余磁通合闸前,变压器铁心中的剩余磁通越大,励磁涌流越大。另外,当剩余磁通Φs的方向与合闸之后自由分量Φmcosα相同时,励磁涌流就会变大[4]。
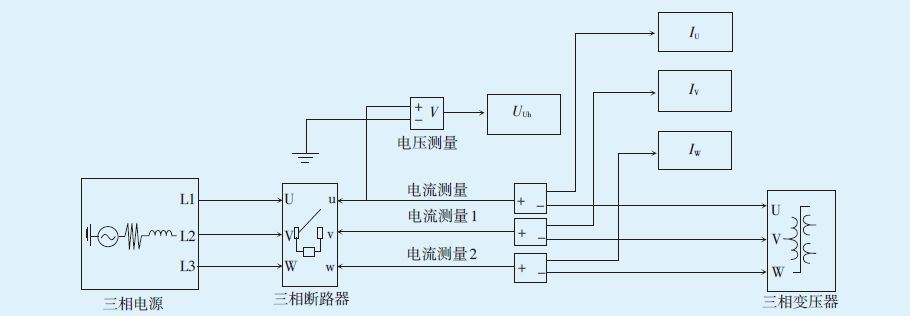
2 励磁涌流仿真根据上述分析,在Simulink工具软件中建立变压器充电仿真模型(如图 1所示),验证励磁涌流的特性[5]。
|
图 1 变压器充电仿真模型 |
某110 kV 变压器A 的接线方式YNyn0d11,容量40 MVA,额定电压(110±8×1.25%)kV/38.5 kV/10.5 kV,额定电流209.9 A/599.8 A/2199.4 A,阻抗标幺值:R1=0.0062,R2=0.0049,R3=0.0050,X1=0.2763,X2=-0.0188,X3=0.1813。图 2 为变压器A 合闸充电在0 s时(即α=0°)的励磁涌流波形仿真结果。
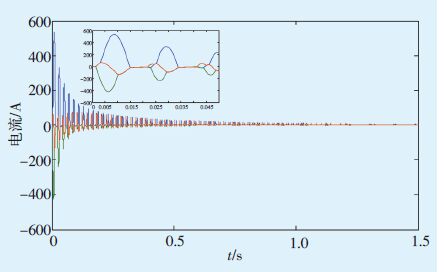
|
图 2 T=1时变压器A在α=0°时的励磁涌流 波形仿真结果 |
将变压器A的容量参数任意增加为63 MVA,其他参数不变时,变压器A在t=0.005 s(1/4个周期即α=90°)时的励磁涌流波形仿真结果见图 3。
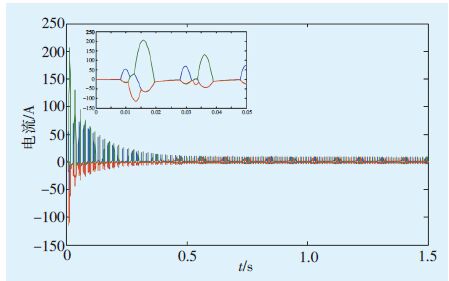
|
图 3 变压器A在α=90°时的励磁涌流仿真波形 |
变压器A在α=0°的励磁涌流波形仿真结果见图 4。
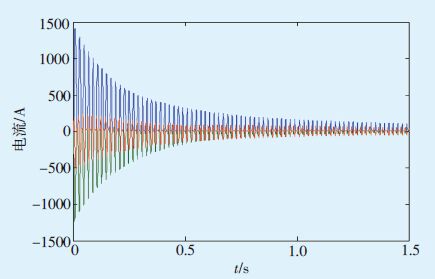
|
图 4 T=7时变压器A在α=0°的励磁涌流波形仿真结果 |
将变压器A中的阻抗标幺值调整为:R1=0.0032,R2=0.0029,R3=0.0030,X1=0.1363,X2=-0.0098,X3=0.0913,将系统短路电流增加约1倍(即系统阻抗约为原来的1/2),仿真结果见图 5。
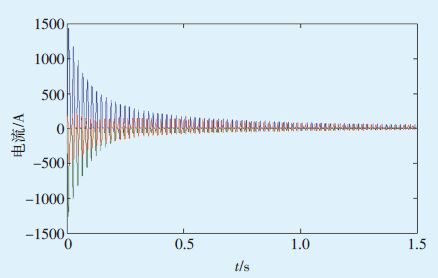
|
图 5 阻抗变小后变压器A的涌流波形 |
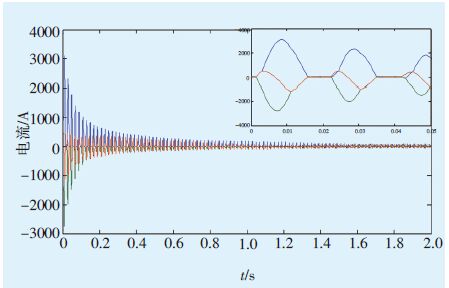
某220 kV变压器B的接线方式YNyn0d11,容量180 MVA,额定电压(220±8×1.25%)kV/121 kV/10.5 kV,额定电流472.4 A/858.9 A/2969.2 A,阻抗标幺值:R1=0.0009,R2=0.0009,R3=-0.0007,X1=0.0833,X2=-0.0057,X3=0.0512。图 6 为变压器B 合闸充电在0 s 时(即α=0°)的励磁涌流波形仿真结果(T=0.5)。
|
图 6 变压器B在α=0°时的励磁涌流波形仿真结果 |
根据公式(3)分析可知,空投变压器时,变压器与电源之间的联系阻抗越大,励磁涌流越小;反之励磁涌流最大值越大[4]。由图 2、图 6可以看出,变压器在α=0°合闸时,励磁涌流最大值出现在0.5个周期以后,此后快速衰减。
由图 2、图 3可以看出,相同条件下,与α=90°合闸时相比,α=0°时合闸的励磁涌流最大,仿真结果与理论分析一致。
比较图 2、图 4可以看出,T 值越大,励磁涌流衰减得越慢。由图 2、图 5可看出,联系阻抗越小,励磁涌流峰值越大。
3 励磁涌流对充电保护定值整定的影响在变压器启动充电时,继电保护定值需考虑能够躲过励磁涌流[6, 7, 8],但有时因躲过励磁涌流的定值设定较大,降低了变压器短路故障时保护动作的灵敏度。为了保证变压器故障保护有足够灵敏度,同时又兼顾励磁涌流的影响,有必要增加1个保护动作时限,以躲过励磁涌流的衰减。整定保护定值时,需要根据励磁涌流幅值及其衰减特性,综合考虑励磁涌流为最大的极端情况和系统的T 值为最大时的涌流衰减情况。
变压器充电保护一般采用过流保护方式躲过励磁涌流,下面以常见的40 MVA变压器(变压器A)充电保护整定为例,仿真分析变压器躲过励磁涌流时的保护动作时限。
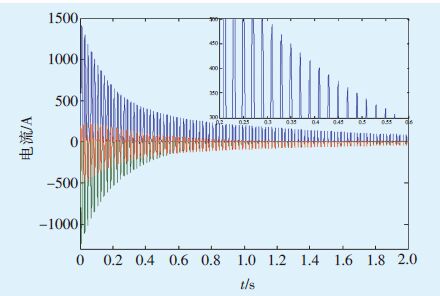
为分析励磁涌流为最大、衰减最慢情况,设置系统大方式时的短路阻抗标幺值为0.1276(换算成短路容量为750 MVA),T=7,在α=0°时合闸,仿真结果见图 7。考虑变压器低压侧故障满足灵敏度Kse=1.5时,充电保护过流定值一次值整定计算结果为462 A。从图 7可以看出,在设定动作时限为0.5 s的情况下即能够可靠躲过励磁涌流。经过在40 MVA变压器上现场实际充电验证此仿真结果,证明该定值整定合理、可靠,可以在提高保护灵敏度的情况下躲过励磁涌流。
|
图 7 极端情况下变压器A充电时的励磁涌流波形 |
变压器励磁涌流的影响因素较多,其衰减速度与合闸回路及变压器绕组阻抗等因素有关[1],变压器保护整定时,需要考虑励磁涌流可能出现的极大值及涌流衰减趋势[9]。通过仿真分析,在设置保护动作时限后,可以保证变压器启动充电时既能可靠躲过励磁涌流,又使保护具有足够的灵敏度,达到提高变压器运行安全稳定性的目的。
| [1] | 何越,熊元新,姜山,等.变压器空载合闸励磁涌流的仿真分析研究[J].电力学报,2010,25(1):34-36. |
| [2] | 国网江苏省电力公司.电力系统继电保护原理及实用技术[M].北京:中国电力出版社,2006:420-426. |
| [3] | 国家电力调度通信中心.继电保护培训教材[M].北京:中国电力出版社,2009:398-404. |
| [4] | 康鑫,王亚娟,吴军.500 kV变压器保护配置与维护探讨[J].陕西电力,2014,42(1):60-64. |
| [5] | 李晓庆,陈尔奎,纪志成.基于Matlab单相变压器的仿真建模及特性分析[J].变压器,2005,42(3):48-54. |
| [6] | 魏凌枫,周剑.采用原子分解法的变压器励磁涌流和故障电流鉴别方法[J].陕西电力,2012,40(6):39-42. |
| [7] | 刘世雄.启备变冷备用快切装置投入分析[J].内蒙古电力技术,2013,31(5):52-56. |
| [8] | 孙向进.变压器励磁涌流对差动保护装置的影响及分析[J].内蒙古电力技术,2007,25(1):52-53. |
| [9] | 崔家佩,孟庆炎,陈永芳,等.电力系统继电保护与安全自动装置整定计算[M].北京:中国电力出版社,1993:194- 238. |
 2015, Vol. 33
2015, Vol. 33 
