电容式电压互感器(CVT)由于具有防止铁磁谐振性能好、测量精度高、安装工程量小,且可兼做系统载波通信用的电容等优势,被广泛应用于110 kV及以上电压等级电网中,其中,无中间抽压端子的叠装式CVT在我国电力系统应用最普遍[1, 2]。CVT的预防性试验也越来越受到相关领域的关注,电容量和介质损耗试验是其中最重要的试验项目。对于多节式CVT,测量若干节电容的电容量和介质损耗通常采用正接线方法单独测量,而对于没有中间抽压端子的叠装式CVT的最下节电容(C1、C2)通常采用自激法测量其电容量和介质损耗[3, 4, 5]。目前,应用自激法选取试验电压时具有随意性,试验人员遵循的电压选取原则不同,大量文献建议选用容量最大的二次绕组为试验绕组,试验电压为2~4 kV[6, 7]。但是由于二次绕组容量有限,若试验电压选取不合适,会导致二次试验绕组过载,甚至烧坏试验绕组。
针对上述问题,文献[8, 9]提出采用降低试验电压或串联二次绕组以减小试验绕组中电流的解决方法。这些方法在很大程度上避免了试验绕组过载问题,但由于都没有考虑励磁单元励磁阻抗分流作用对二次绕组电流的影响,以至于所加电压过低,影响试验结果的精度。
本文在考虑励磁回路分流作用影响的前提下,对采用自激法时试验电压的计算方法进行了改进。
1 CVT自激法测试原理自激法是对CVT电磁单元的二次绕组加压,经过电磁单元变压器感应到高压侧,实现对最下节电容(C1、C2)电容量和介质损耗的测量。本文以TYD220/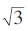 -0.01W3型CVT的下节结构(见图 1)为例分析测试原理。试验原理见图 2所示。
-0.01W3型CVT的下节结构(见图 1)为例分析测试原理。试验原理见图 2所示。
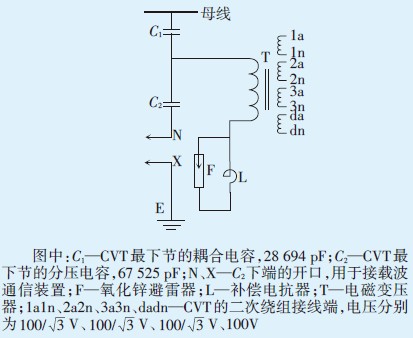 |
图1 TYD220/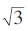 -0.01W3型CVT最下节结构图 -0.01W3型CVT最下节结构图 |
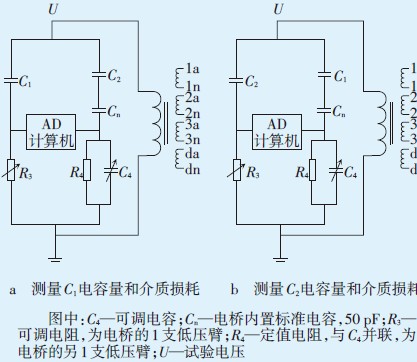 |
图2 采用自激法测量C1、C2电容量和介质损耗试验原理图 |
测量C1的电容量和介质损耗时,C2与标准电容Cn串联构成电桥的标准电容桥臂,串联后的等值电容值C等1可以由式(1)求得:

同理,测量C2的电容量和介质损耗时,等值电容值C等2可以由式(2)求得:

串联后的等值电容与Cn的偏差CΔ可由式(3)求得:
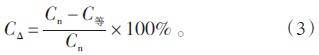
经计算,C等1和C等2的偏差分别为0.08%、0.18%,在工程允许偏差范围之内。
2 传统二次绕组试验电压选取方法分析本文以单绕组加压2 kV[10]为例,对试验电压二次绕组的过载情况进行分析。二次绕组的额定电流可由式(4)求得:

式中S2n—二次绕组的额定容量,150 VA;
U2n—二次绕组的额定电压,V。
计算得出1a1n、2a2n、3a3n二次绕组的额定电流均为2.6 A,dadn的额定电流为1.5 A。
根据串联电容分压原理可知,CVT正常工作时分压电容两端的电压可由式(5)求得:
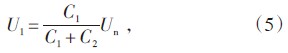
式中Un—CVT正常工作时最下节电容串承受的额定相电压有效值,110/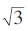 V。
V。
计算得出:电磁单元一次电压U1 为18.94 kV。在此基础上,以1a1n绕组为例,电磁单元变压器的变比可由式(6)求得:

计算结果为k=328.04。
当电桥平衡,测量C1、C2电容量和介质损耗时电流流通情况见图 3所示。
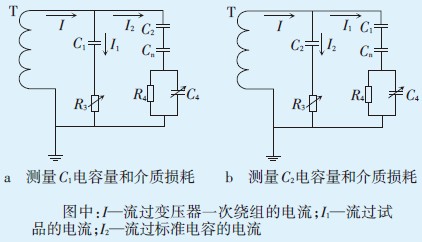 |
图3 测量C1、C2电容量和介质损耗时电流分布图 |
根据图 3a分析试验过程中电流分布情况,试品的阻抗Z1、标准电容桥臂阻抗Z2远大于可调电阻R3桥臂的阻抗Z3、可调电容C4桥臂的阻抗Z4[11],即I1、I2可以近似认为是容性电流,I1与I2同向,此时流过变压器一次绕组的电流I=I1+I2。
由于C2与Cn串联后的等值电容远小于C1,因此I1≫I2,流过变压器一次绕组的电流I≈I1。当试验电压U 为2 kV时,流过变压器一次绕组的电流值计算公式见式(7):

式中ω—试验电压角频率,100π。
计算结果为I=18.02 mA。
同理,测量C2的电容量和介质损耗时,根据图 3b,求得流过变压器一次绕组的电流I=42.41 mA。分析2次试验的结果可知,测量C2电容量和介质损耗时流过变压器一次绕组的电流较大,根据变压器绕组电流与匝数的关系可以求得此时二次侧试验绕组的电流为13.91 A,是二次绕组1a1n额定电流的5.35 倍。可见,选择单绕组作为试验绕组时,如果试验电压选择不当,会导致试验绕组过载,甚至会烧毁试验绕组。
采用降低试验电压的方法可以成比例降低流过试验绕组的电流,能有效解决试验绕组过载问题,但该方法在一定程度上降低了测量精度,影响试验结果的准确度[8]。二次绕组串联加压法减小了电磁单元变压器的变比,在其一次电流不变的情况下,流过二次绕组的电流将会减小,起到了保护试验绕组的作用。但传统的二次绕组串联加压法在分析流过二次绕组电流时没有考虑励磁回路分流作用的影响,导致流过试验绕组的电流计算值不准确,在一定程度上影响了试验结果的可靠性。
3 考虑励磁回路分流的试验电压计算方法本文研究CVT自激法的试验电压时,以二次绕组不过载为原则,充分考虑电磁单元励磁阻抗分流作用对试验绕组电流的影响,运用基于向量的基尔霍夫电流定律(KCL)定量分析流过试验绕组电流与试验电压的关系。励磁单元变压器的T型等值电路图如图 4所示(将各参数折算到变压器低压侧)。
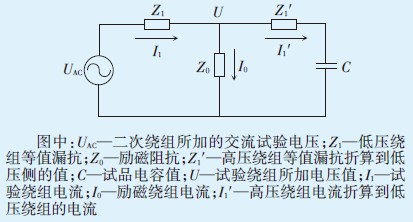 |
图4 励磁单元变压器T型等值电路图 |
由图 4可知各支路电流满足I1=I0+I1′。
一般由于负载电容C 的等值容抗远大于Z1′,因此工程处理中可以认为I1′为容性电流。而励磁回路的等值电阻与其等值电抗相比可以近似忽略,因此励磁电流I0可近似为感性电流。综上所述,I1、I1′同向,而I0与I1、I1′反向。
假设励磁电流I0与I1′的比值为a(考虑励磁回路分流后a < 1),则根据基尔霍夫电流定律计算试验绕组电流的有效值方法见式(8):

由式(8)可知,实际流过试验绕组的电流比采用传统计算方法得出的计算结果小,该值与a 有关,即传统计算方法在确保试验绕组不过流的前提下求得的试验电压偏小,不利于发现绝缘缺陷[12]。
4 现场试验分析采用AI-6000K型自动抗干扰精密介质损耗测量仪测量CVT电容量和介质损耗,该装置内置标准电容量50 pF,最高试验电压为10 kV。以对1a1n、2a2n、3a3n 3个绕组串联加压为例进行分析,根据公式(6)计算变比为109.35,不考虑励磁绕组分流作用的影响时,如果试验电压为1 kV,则根据公式(4)、(7)可以求得励磁变压器的高压绕组最大电流为21.21 mA,此时试验绕组电流为2.32 A。
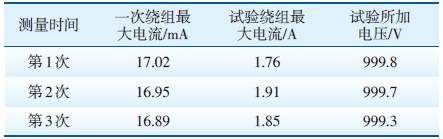
对某220 kV CVT下节进行试验,分别对CVT中间单元高压侧电流和试验绕组电流进行了测量(1a1n、2a2n、3a3n 3个绕组串联加压),3次测量数据见表 1所示。
| 表 1 CVT绕组电流试验结果 |
由表 1数据计算后得出,流过高压绕组和试验绕组最大电流平均值分别为16.95 mA、1.84 mA,比不考虑励磁绕组分流作用时的电流计算值小20.08%、20.69%,即试验中,最大试验电压值可以增加约20%。
据此对试验电压值进行校正,当1a1n、2a2n、3a3n 3个绕组串联加压时,试验绕组允许最大电流值为2.6 A,计算求得一次绕组允许电流值为23.78mA,校正前试验电压值为1.12 kV,校正后试验电压值约为1.4 kV,即只要试验电压不超过1.4 kV,流过试验绕组的电流值都不会超过允许值。
此时,图 1中N点的电压也不会超过允许电压值(4 kV)[13],确保N点绝缘不被破坏,试验绕组的电压也不会超过额定值,整个试验过程不会对设备和仪器的安全造成威胁。
5 结语在采用自激法测量CVT电容量和介质损耗试验中,传统的试验电压计算方法没有考虑变压器励磁回路分流作用的影响,导致计算出的试验电压允许值偏小。对此本文提出改进的试验电压计算方法,并进行现场试验验证,不考虑励磁回路分流时求得的试验电压值为1.12 kV,考虑变压器励磁回路分流作用影响时试验电压比采用传统方法计算的电压高约20%,即约为1.4 kV,证明了改进算法的准确性。
本文提出的计算方法提高了CVT试验电压值的计算准确性,有利于发现CVT绝缘缺陷,对全面掌握CVT的运行状态参数有重要意义。该方法有效克服了传统计算方法存在的弊端,为CVT自激法选择二次绕组试验电压提供了可靠的理论依据。
| [1] | 王亚平,岳永刚.CVT自激法测试原理及其试验电压的选取[J].内蒙古电力技术,2010,28(6):17-20. |
| [2] | 陈德兴,谢春雷.电容式电压互感器故障分析及防范措施[J].电力电容器,2006,17(6):44-45. |
| [3] | 李继强.测量CVT电容量和介质损耗时二次侧试验电压的选取方法分析[J].内蒙古电力技术,2012,30(3):113-118. |
| [4] | 韩桂芝.采用CVT自激法测量电容式电压互感器的[J].内蒙古电力技术,2005,23(2):61-62. |
| [5] | 任玉民,卢绍毅,白丽.电容式电压互感器介损的测量方法[J].内蒙古电力技术,2009,27(S):122-123. |
| [6] | 王永军.CVT的介损和电容量测试方法研究及应用[D].北京:华北电力大学,2012. |
| [7] | 李俊,李帆,汪司珂.基于自激法测电容式电压互感器检测技术的分析研究[J].电测与仪表,2013,50(6):49-52. |
| [8] | 李涛,杜晓平,刘焕光.电容式电压互感器自激法的测试及误差分析[J].电力系统保护与控制,2009,37(5):31-33. |
| [9] | 李柯.电容式电压互感器绝缘诊断方法[J].水利水电技术,2013,44(9):100-104. |
| [10] | 张晓惠.电气试验[M].北京:中国电力出版社,2010:218-220. |
| [11] | 周泽存,沈其工,方瑜,等.高电压技术[M].北京:中国电力出版社,2007:54-62. |
| [12] | 陈化钢.电力设备预防性试验方法及诊断技术[M].北京:水利水电出版社,2009:432-454. |
| [13] | 赵京武,李红林.用自激法测试电容式电压互感器及误差分析[J].高压电器,2000,15(2):49-51. |
 2015, Vol. 33
2015, Vol. 33