2. 太原理工大学计算机科学与技术学院, 太原034000
2. Taiyuan University of Technology, Taiyuan 034000, China
近年来,由于电力系统的规模不断扩大,同时易受到外界各种因素的干扰(如雷击等),使得对电力系统的操作和控制更加复杂。电力系统受到外界干扰后,可能会导致发电机电磁功率和机械转速瞬间发生变化,影响电力系统的稳定性。因此在电力系统中应采用稳定的控制器,以防止发电机受到干扰,影响发电机稳定运行。
线性最优励磁控制器(LOEC)已在电力系统中得到迅速应用,目前该技术已趋于成熟。研究表明,在不同的干扰情况下励磁控制系统的阻尼可以增强,LOEC可以提高远距离输电系统的静态稳定性,也可以改善系统遭受小扰动时的阻尼特性。陈中研究了稳态运行点的小扰动稳定性[1]。马幼捷、刘进华等人指出小扰动稳定域的边界可能包含Hopf分叉HB(Hopf Bifurcation)[2]。文献[3]针对控制器饱和与扰动的线性模型,提出了基于二次型李雅普诺夫函数的吸引域估计方法。文献[4]进一步提出了以椭球吸引域体积为指标确定小扰动稳定域边界的新算法,分析了负荷模型对小扰动稳定域的影响。文献[5]提出了对电力系统中Web服务进行自动故障分析的说明。
本文在传统的LOEC基础上,设计了一种基于机械式无阻尼振荡频率不变性的新型阻尼线性最优励磁控制器(DLOEC),之后在单机无穷大电力系统(SMIB)中进行仿真,结果表明,本文设计的DLOEC可以有效提高电力系统的稳定性。1 线性最优励磁控制器的设计原理
发电机系统的状态方程用四阶方程描述[6],对于快速励磁系统,励磁时间常数Te≈0,UR为控制变量,则系统的状态方程简化为三阶形式。对于LOEC,状态方程的设计标准形式为Ẋ =AX+BU,其中,A为n×n阶状态系数矩阵,B为n×r阶控制系数矩阵,X为n维状态向量,U为r维控制向量,系统的状态方程如公式(1)所示[6]:
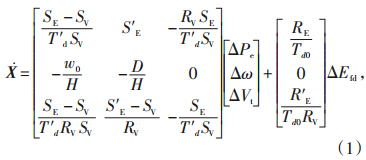
Δω—转子角速度的偏差;
ΔVt—同步发电机的端电压偏差;
ΔEfd—磁场绕组电压的偏差;
T'd—定子绕组闭路时励磁绕组时间常数;
w'0—转子同步角速度;
SE—发电机空载电动势,
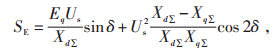
S'E—暂态电动势;

SV—机端电压,
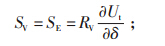
RV—励磁调节器的输出电压,
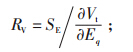
RE—励磁调节器电流,

R'E—励磁调节器暂态电流,
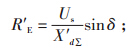
Td0—定子绕组开路时,励磁绕组的时间常数;
D—发电机除去励磁调节作用外,其他固有阻尼作用的等值常数;
H—转子惯性时间常数。
对于快速励磁系统,其二次型性能指标的设计如公式(2)所示:

Q—状态向量X的权重矩阵;
R—控制向量U的权重矩阵。
基于最优控制理论[7, 8],反馈系数矩阵为:K=R-1BTP,其中,P为公式(3)中Riccati方程的解。


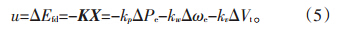
LOEC的常规设计中,会首先给出矩阵R和Q,从公式(3)中可以得到矩阵P,从公式(4)中可以得到反馈系数矩阵K。如果Q改变,则K也会发生相应的变化。可以通过反复试验来获得Q值,这种方法相对简单、低效。试验的步骤为:首先,选择几种不同的Q值,从公式(3)、(4)中分别获得矩阵P、K;其次,比较控制的效果,选择矩阵Q和K,通过电力系统仿真,得到动态模拟测试的控制效果。
这种方法的缺点是:矩阵Q的选择是随机的,导致不同矩阵Q对系统的控制所花费的时间比较长,而且成本也比较高。另外,矩阵Q的选择和系统的阻尼之间的关系目前尚不清楚。2.2 基于阻尼系数ξn的DLOEC设计2.2.1 无阻尼机械振荡频率的不变性
同步发电机的线性转子运动的方程如公式(6)所示:
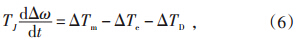
通过使用拉普拉斯变化,并且考虑Δω=sΔδ w'0,其中,s为得到的反馈系数矩阵相应的特征向量。由公式(6)可以得出:
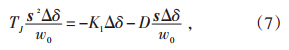
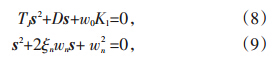
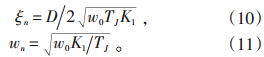
本文设计的线性最优励磁控制器,可以通过增加附加励磁控制的方法得到ξn,wn保持不变。从LOEC中通过比较特征多项式的期望值,可以得到反馈系数矩阵K的值。这就是DLOEC的设计方法,主要的算法如下。
(1)解出wn。在没有LOEC的基础上解出机械模式特征值,假设该特征值为σ±jw,则无阻尼机械振荡频率为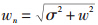 。
。
(2)获得闭环系统的期望特征值。假设期望阻尼系数是ξn,则闭环系统的预期机械模式特征值为 。由于该系统是个三阶系统,需要解决最后真正的根。
。由于该系统是个三阶系统,需要解决最后真正的根。
(3)获得反馈系数矩阵K。在没有LOEC中,系统的状态方程为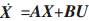 ,预期的特征值为λi(i=1,2,3),预期的特征多项式为
,预期的特征值为λi(i=1,2,3),预期的特征多项式为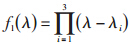 。当进入闭环系统后,系统的状态方程为
。当进入闭环系统后,系统的状态方程为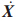 =(A-BKX)+BV,其中,V为参考输入矢量。闭环系统的特征多项式为f2(λ)=det[λI-(A-BK)]。令f1(λ)=f2(λ),然后进行相应系数的比较,可以得出kp(λ),kw(λ),kv(λ)的值,从而得到反馈系数矩阵K。3 仿真分析3.1 系统模型
=(A-BKX)+BV,其中,V为参考输入矢量。闭环系统的特征多项式为f2(λ)=det[λI-(A-BK)]。令f1(λ)=f2(λ),然后进行相应系数的比较,可以得出kp(λ),kw(λ),kv(λ)的值,从而得到反馈系数矩阵K。3 仿真分析3.1 系统模型
本文采用单机无穷大电力系统证明线性最优励磁控制器设计的有效性。该发电机和传输线路的参数如下:发电机d轴同步电抗Xd=1.305,d轴暂态电抗X'd=0.296,q轴同步电抗Xq=0.474,H=3.2,D=8.922,Td0=10。对于输电线路,线路T的电抗XT=0.01,线路L的电抗XL=0.73,电力系统功率因数cosφ=0.975,电磁功率P0=0.75(p.u.)。
则在没有LOEC的系统的状态方程为:

该系统的特征值为-1.4611±6.5102i,-0.0634,无阻尼机械振荡频率wn=6.6721,阻尼系数ξn=0.2190。
为了方便比较,本文设计了2个励磁控制器驱动DLOEC1和DLOEC2,分别对应阻尼系数ξn1 和ξn2 ,其中,ξn1=0.05,ξn2=0.5。显然ξn1<ξn<ξn2,所以DLOEC1降低了本文设计的线性最优励磁控制系统的阻尼效果,而DLOEC2提高了系统的阻尼效果。
基于本文DLOEC的算法,对应的反馈系数矩阵K1和K2计算过程为:
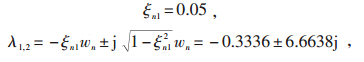
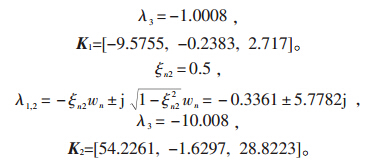
为了显示DLOEC性能,对1个典型的单机无穷大系统干扰描述如下。严重的三相短路故障的情况说明如下:第一阶段:系统处于故障前稳态;第二阶段:当t=0.4s时,发生三相短路故障;第三阶段:当t=0.5s时,进行自动排除故障;第四阶段:该系统处于后故障状态。3.3 结果分析
对于电力系统来说,三相短路故障是1个严重的故障,会被看成1个很大的干扰。当t=0.4s时,发生三相短路故障,电磁功率Pe会急剧降低。当t=0.5s时,进行自动排除故障,电磁功率急剧增加,开始发生振荡,达到阻尼效果,系统逐渐恢复稳定。
对于DLOEC2,在1.1s时电磁功率的振荡保持稳定状态,1.8s时转子角速度的振荡保持稳定状态,经过1个循环后都会消失。显而易见的是,DLOEC2的控制效果最好。因为DLOEC2从0.2190增到0.5,增加了控制系统的阻尼系数。DLOEC1的控制效果最差,并且其控制动作降低了系统的阻尼特性,这是因为闭环阻尼系数为ξn1,而ξn1<ξn。而PSS要求更多的时间和更多的振动,图 1和图 2分别表示了电磁功率和转子角速度对应的响应。
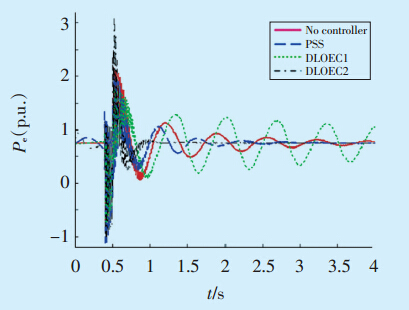 |
图 1 电磁功率响应 |
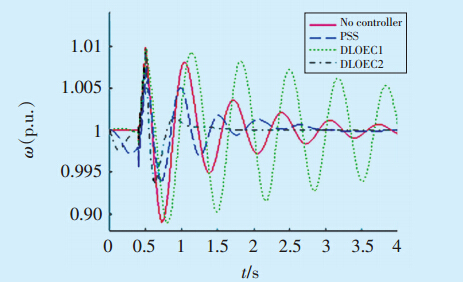 |
图 2 转子角速度响应 |
本文设计了一种新的阻尼线性最优励磁控制器(DLOEC)。首先,分析了传统的LOEC及其设计方法,然后根据阻尼系数设计了阻尼线性最优励磁控制器。从PSS的基于机械模式特征值的设计方法可以看出,当阻尼系数提高时,无阻尼机械振荡频率可保持不变。仿真试验结果表明,该控制器可以提供阻尼给线性励磁控制系统,提高了电力系统的动态性能,并且无需考虑Q矩阵的选择。
| [1] | 陈中.电力系统下干扰稳定实时控制[J].电力自动化设备,2012,32(3):42-46. |
| [2] | 马幼捷,刘进华,周雪松,等.含STATCOM的风电系统鞍结分岔边界追踪及其非线性解析表达[J].电力自动化设备,2012,32(3):90-93. |
| [3] | 王康,辛焕海,雷金勇,等.考虑控制器饱和与扰动的电力系统稳定域估计[J].中国电机工程学报,2010,30(31):70-76. |
| [4] | 李江,魏丹萍,张少杰,等.负荷模型对饱和系统小扰动稳定域的影响[J].电力自动化设备,2011,31(10):23-27. |
| [5] | Mustarum Musaruddin, Rastko Zivanovic. Web Servicesfor Automated Fault Analysis in Electrical Power Systems[J]. Advances in Information Sciences and Service Sciences,2010,2(3):76-81. |
| [6] | Han Yingduo, Wang Zhonghong. Power system optimaldecentralized coordinated control[M].Beijing: TsinghuaUniversity Press, 1997: 23-30. |
| [7] | 魏阳,张俊芳,卫鹏.线性最优励磁控制器的设计与仿真[J].电力科学与技术学报,2013,28(2):44-51. |
| [8] | 刘明锦.基于线性最优控制理论的励磁系统的设计及仿真[J].电气开关,2010(1):52-55. |
 2015, Vol. 33
2015, Vol. 33 
